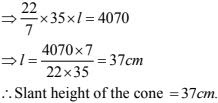RD Sharma Solutions for Class 9 Chapter 20 Surface Area of Volume of a Right Circular Cone Exercise 20.1

Chapter 20 Surface Area of Volume of a Right Circular Cone RD Sharma Solutions Exercise 20.1 Class 9 Maths

Chapter Name	RD Sharma Chapter 20 Surface Area of Volume of a Right Circular Cone Exercise 20.1
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 20.2
Related Study	NCERT Solutions for Class 10 Maths

Exercise 20.1 Solutions

1. Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.

Solution

Given that 
Radius of its base is 21 cm 
Slant height = 60 cm 
WKT, Curved surface area of a cone = πrl
∴ Curved surface area = 22/7 × 21 × 60
= 3960 cm² 

2. The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface. 

Solution

Given, 
Radius of cone = 5cm  = r 
Height of a cone = 12 m = h 

3. The radius of a cone is 7 cm and area of curved surface is 176 cm² . Find the slant height. 

Solution

Given 
Radius of a cone (r) = 7 cm. 
Let 'l' be the slant height of a cone 
∴ Curved surface area = πrl. 
⇒ 176 = π × 7 × l
⇒ l = 176/7π = (176 × 7)/(7 × 22) = 8 cm.

4. The height of a cone is 21 cm. Find the area of the base if the slant height is  28 cm. 

Solution

Given that 
Slant height 'I' = 28 m. 
Height of cone (h) = 21 cm 

5. Find the total surface area of a right circular cone with radius 6 cm and height 8 cm. 

Solution

6. Find the curved surface area of a cone with base radius 5.25 cm and slant height 10 cm. 

Solution

Given that, 
Radius of a base of a cone = 5.25 cm 
Slant height of cone = 10 cm 
Curved surface area of cone = πrl 
= 22/7 × 5.25 × 10 cm² 
= (22 × 0.75 × 10) cm² = 165 cm² 
Thus, the curved surface area of a cone is 165 cm² 

7. Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m 

Solution

Given that, 
Radius of base of cone = 24/2 = 12 m 
Slant height of cone  = 21m.

8. The area of the curved surface of a cone is 60π cm² . If the slant height of the cone be 8 cm, find the radius of the base ? 

Solution

Given that 
Curved surface area of cone = 60 π cm² 
∴ Slant height of cone (l) = 8 cm. 
i.e, πrl = 60 π 
⇒ π× r × 8 = 60π 
⇒ r = 60/ 8 = 7.5 
∴ Radius of cone = 7.5 cm 

9. The curved surface area of a cone is 4070 cm² and its diameter is 70 cm. What is its slant height ? (Use it π 22/7 )

Solution

Given diameter = 70 cm 
⇒ 2r = 70 cm 
⇒ r = 35 cm
Now, curved surface area = 4070 cm² 
⇒ πrl = 4070 
Where r = radius of the cone 
l = slant height of the cone 
∴ πrl = 4070 

10. The radius and slant height of a cone are In the ratio of 4 : 7. If its curved surface area is  792 cm² , find its radius. (Use it π = 22/7)

Solution Given that, 
Curved surface area = πrl = 792.
Let the radius (r) = 4x 
Height (h) = 7x 
Now, CSA  = 792 

11. A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm.

Find the area of the sheet required to make 10 such caps.

Solution

Given that, 
Radius of conical cap (r) = 7 cm. 
Height of conical cap (h) = 24 cm. 

12. Find the ratio of the curved surface areas of two cones if their diameters of the bases are

equal and slant heights are in the ratio 4 : 3.

Solution

Given that, 
Diameter of two cones area equal 
∴ Their radius are equal 

13. There are two cones. The curved surface area of one is twice that of the other. The slant

height of the later is twice that of the former. Find the ratio of their radii.

Solution

Let curved surface area off 1st cone = 2x 
CSA of 2nd cone = x 
and slant height of 1st cone = h 
and slant height of 2nd cone = 2h

14. The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surfaces.

Solution

Given that, 

Diameters of two cones are equal 

∴ Their radius are also equal i.e., 

15. Curved surface area of a cone is 308 cm² and its slant height is  14cm. Find the radius of the base and total surface area of the cone. 

Solution

(i) Given that, 

Slant height of cone = 14cm 

Let radius of circular end of cone = r.
Curved surface area of cone = πrh 

16. The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find

the cost of white-washing its curved surface at the rate of Rs. 210 per l00 m².

Solution

Given that, 

Slant height of conical tomb (l)  = 25 ,

Base radius (r) of tomb = 14/2 = 7 . 

CSA of conical length tomb = πrl 
= (22/7 × 7 × 25)m² 
= 550 m² 
Cost of white - washing 100 m² area = Rs. 210 
Cost of white - washing  550 m² area = Rs. (210 × 550)/100 = Rs.  1155. 
Thus the cost of white washing total tomb = Rs. 1155.

17. A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1m² canvas is Rs. 70, find the cost of the canvas required to make the tent. 

Solution

(i) Given that 

Height of conical tent(h) = 10 m
Radius of conical tent (r) = 24 m.

Let slant height of conical tent be l 

18. A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of

cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is

16 m above the ground. Find the area of the canvas required for the tent.

Solution

Given that, 

Diameter of cylinder =24 m 

∴ Radius = diameter/2 = 24cm/2 = 12 cm 

Also Radius of cone = 12 m.

Height of cylinder = 11 m 

Height of cone = 16 - 11 = 5m 

19. A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105

m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m

wide to make the required tent.

Solution

Given diameter = 105 m 
Radius = 105/2 m = 52.5 m 
∴ Curved surface area of circus tent = πrl + 2πrh 

∴ Length of the canvas equation for tent = Area of canvas/width of canvas = 9735/5 = 1947 m 

20. The circumference of the base of a 10 m height conical tent is 44 metres. Calculate the length of canvas used in making the tent if width of canvas is 2 m. (Use it π = 22/7)

Solution

WKT, CSA of cone = πrl 

Given circumference = 2πr 
⇒ 2 × 22/7 × r = 44 
r/7 = 1 
r = 7m 

21. What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm (Use it π = 3.14)

Solution

Given that, 

Height of conical tent (h) = 8 m. 
Radius of base of tent (r) = 6m. 

Let the length of tarpaulin sheet require be L 
As 200 m will be wasted, So effective length will be (L - 0.2m)
Breadth of tarpaulin = 3m 
Area of sheet = CSA of sheet 

(L × 0.2 m × 3)m = 188.40 m² 
⇒ L - 0.2 m = 62.8 m 
⇒ L = 63 m 
Thus, the length of the tarpaulin sheet will be = 163 m. 

22. A bus stop is barricated from the remaining part of the road, by using 50 hollow cones made of recycled card-board. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m² , what will be the cost of painting all these cones.  (Use π = 3.14 and √1.04 = 1.02)

Solution

Radius of cone (r) = 40/2 = 20 m = 0.2 m.

Height of cone = 1 m. 

23. A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.

Solution

Let us assume radius of cone = r
Also, radius of cylinder = r .
Height of cone = h
And, height of cylinder = h