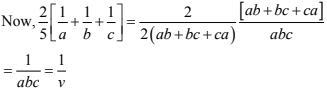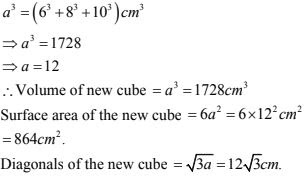Chapter 18 Surface Area and Volume of Cuboid and Cube RD Sharma Solutions Exercise 18.2 Class 9 Maths

Chapter Name | RD Sharma Chapter 18 Surface Area and Volume of Cuboid and Cubes Exercise 18.2 |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 18.2 Solutions
1. A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold?
Solution
Given length = 6cm
Breath = 56 m
Height = 4.5 m
Volume of the tank = l × b × h = 6 × 5(4.5) = 135 m3
It is given that
1m3 = 1000 liters
∴ 135m2 = (135 × 1000) liters
= 135000 liters
∴ The tank can hold 135000 liters of water.
2. A cubical vessel is 10m long and 8 m wide. How high must it be made to hold 380 cubic metres of a liquid ?
Solution
Given that
Length of vessel (l) = 10 m
Width of vessel (b) = 8m
Let height of the cuboidal vessel be 'h'
Volume of vessel = 380 m2
∴ l × b × h = 380
⇒ 10 × 8 × h = 380
⇒ h = 4.75
∴ height of the vessel should be 4.75 m.
3. Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3m deep at the rate of Rs. 30 per m3.
Solution
Given length of the cuboidal Pit(l) = 8m
Width (b) = 6 m
Depth (h) = 3m
Volume of cuboid pit = l × b × h = (8 × 6×3)m3 = 144m3
Cost of digging 1m3 = Rs. 30
Cost of digging 144 m3 = 144(Rs. 30) = Rs. 4320.
4. If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that
1/V = 2/s(1/a+ 1/b + 1/c)
Solution
Given that
Length = a
Breadth = b
Height = c
Volume (v) = l × b × h
= a × b × c = abc
Surface area = 2(lb + bh + hl)
= 2(ab + bc + ac)
5. The areas of three adjacent faces of cuboid are x, y and z. If the volume is V, prove that
V2 = xyz.
Solution
Let a, b, d be the length, breath and height of cuboid then,
x = ab
y = bd,
z = da, and
v = abd [v = l × b × h]
⇒ xyz = ab × bc × ca = (abc)2
And v = abc
v2 = (abc)2
⇒ v2 = xyz
6. If the area of three adjacent faces of a cuboid are 8 cm3 , 18 cm3 and 25cm3 . Find the volume of the cuboid.
Solution
WKT, if x, y, z denote the areas of three adjacent faces of a cuboid
⇒ x = l × b, y = b × h, z = l × h
Volume V is given by
V = l × b × h
Now, xyz = l × b × b × h × l × h = v2
Here x = 8
y = 18
And z = 25
∴ v2 = 8 × 18 × 25 = 3600
⇒ v = 60 cm3
7. The breadth of a room is twice its height, one half of its length and the volume of the room is 512cu. m. Find its dimensions.
Solution
We have,
b = 2h and b = 1/2
⇒ l/2 = 2h
⇒ l = 4h
⇒ l = 4h, b = 2h
Now,
Volume = 512 m3
⇒ 4h × 2h × h = 512
⇒ h3 = 64
⇒ h = 4
So, l = 4 × h = 16 m
b = 2 × h = 8m
And h = 4m
8. A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
Solution
Radius of water flow = 2 km per hour = (2000/60) m/min
= (100/3) m/min
Depth (h) of river = 3m
Width (b) of river = 40m
Volume of water followed in 1 min = 100/3×40 ×3 m3 - 4000 m3
Thus, 1 minute 4000 m3 = 4000000 liters of water will fall in sea.
9. Water in a canal 30 cm wide and 12 cm deep, is flowing with a velocity of l00 km per hour. How much area will it irrigate in 30 minutes if 8 cm of standing water is desired?
Solution
Given that,
Water in the canal forms a cuboid of
width (h) = 300 cm = 3m
height = 12 cm = 1.2 m
length of cuboid is equal to the distance travelled in 30 min with the speed of 100 km per hour
∴ length of cuboid = 100 × 30/60 km = 50000 meters
So, volume of water to be used for irrigation = 50000 × 3 × 1.2m3
Water accumulated in the field forms a cuboid of base area equal to the area of the field and height equal to 8/100 meters
∴ Area of field × 8/100 = 50000 × 3 ×1.2
⇒ Area of field = (50000 ×3 × 1.2 ×100)/8
= 2250000 meters
10. Three metal cubes with edges 6 cm, 8 cm and 10 cm respectively are melted together and formed into a single cube. Find the volume, surface area and diagonal of the new cube.
Solution
Let the length of each edge of the new cube be a cm
Then,
11. Two cubes, each of volume 512 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Solution
Given that,
Volume of cube = 512 cm3
⇒ side3 = 512
⇒ side3 = 83
⇒ side = 8cm
Dimensions of new cuboid formed
l = 8 + 8 = 16cm, b = 8cm, h = 8cm
Surface area = 2(lb + bh + hl)
= 2[16 (8) + 8(8) + 16(8)]
= 2[256 + 64]
= 640 cm2
∴ Surface area is 640 cm2
12. Half cubic meter of gold - sheet is extended by hammering so as to cover an area of 1 hectare. Find the thickness of the gold - sheet.
Solution
Given that,
Volume of gold = 0.5 m3
Area of gold sheet = 1 hectare = 10000 m2
∴ Thickness of gold sheet = Volume of gold/Area of gold sheet
Thickness of gold sheet = 1/200 cm.
13. A metal cube of edge 12 cm is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 6 cm and 8 cm, find the edge of the third smaller cube.
Solution

14. The dimensions of a cinema hall are 100 m, 50 m and 18 m. How many persons can sit in the hall, if each person requires 150 m3 of air ?
Solution
Given that,
Volume of cinema hall = 100 × 50 × 18 m3
Volume air required by each person = 150 m3
Number of person who can sit in the hall = Volume of cinema hall/volume of air req. each person
= (100 × 50 × 18)/150 = 600m3 [∵ V = l × b × h]
∴ number of person who can sit in the hall
= 600 members
15. Given that l cubic cm of marble weighs 0.25 kg, the weight of marble block 28 cm in width and 5cm thick is112 kg. Find the length of the block.
Solution
Let the length of the block be 1 cm
Then, volume = l × 28 × 5 cm3
∴ weight = 140l ×0.25 kg
According to the question
⇒ 112 = 1401 ×0.25
⇒ l = 112/(140 ×0.25) = 3.2 cm
16. A box with lid is made of 2 cm thick wood. Its external length, breadth and height are 25 cm, 18 cm and 15 cm respectively. How much cubic cm of a liquid can be placed in it ? Also, find the volume of the wood used in it.
Solution
Given external dimensions of cuboid are
l = 25 cm, b = 18 cm, h = 15 cm
∴ External volume = l × b × h
= 25 × 18 × 15 cm3
= 6750 cm3
Internal dimension of cuboid.
l = 25 - 2 × thickness = 25 - 4 = 21 cm
h = 15 - 4 = 11 cm
Internal volume = l × b × h
= 21 × 14 × 11 cm3
= 3234 cm3
∴ Volume of liquid that can be placed = 3234 cm3
Now, volume of wood = external volume - Internal volume
= 6750 - 3324
= 3516 cm3
17. The external dimensions of a closed wooden box are 48 cm, 36 cm, 30 cm. The box is made of 1.5 cm thick wood. How many bricks of size 6 cm × 3 cm × 0.75 cm can be put in this box ?
Solution
Given internal dimensions are:
l = 48 - 2 × thickness = 48 - 3 = 45 cm
b = 36 - 3 = 33 cm
h = 30 - 3 = 27 cm
∴ Internal volume = 45 × 33 × 27 cm3
Volume of brick = 5 × 3 ×0.75 cm3
Hence, number of bricks = Internal volume/volume of 1 brick
= (45× 33 × 27)/(6 × 3 × 0.37)
= 38880/13.5
= 2970
∴ 2970 bricks can be kept inside the box.
18. How many cubic centimeters of iron are there in an open box whose external dimensions are 36 cm, 25 cm and I 6.5 cm, the iron being 1.5 cm thick throughout? If I cubic cm of iron weighs 15g, find the weight of the empty box in kg.
Solution
Outer dimensions
l = 36 cm
b = 25 cm
h = 16.5 cm
Inner dimensions
l = 36 - (2 × 1.5) = 33 cm
b = 25 - 3 = 22 cm
h = 16.5 - 1.5 = 15 cm
Volume of iron = outer volume - inner volume
= (36 × 25 × 16.5 - 33 × 12 × 15) cm3 = 3960 cm3
Weight of iron = 3960 × 1.5 gm = 59400 gm = 59.4 kg
19. A cube of 9 cm edge is immersed completely in a rectangular vessel containing water. If the dimensions of the base are 15 cm and 12 cm, find the rise in water level in the vessel.
Solution

20. A rectangular container, whose base is a square of side 5 cm, stands on a horizontal table, and holds water up to 1 cm from the top. When a cube is placed in the water it is completely submerged, the water rises to the top and 2 cubic cm of water overflows. Calculate the volume of the cube and also the length of its edge.
Solution
Let the length of each edge of the cube be x cm
Then,
Volume of cube = volume of water inside the tank + volume of water that over flowed
x3 = (5 × 5 ×1) + 2 = 25 + 2
x3 = 27
x = 3 cm
Hence, volume of cube = 27 cm3
And edge of cube = 3cm.
21. A field is 200 m long and 150 m broad. There is a plot, 50 m long and 40 m broad, near the field. The plot is dug 7 m deep and the earth taken out is spread evenly on the field. By how many meters is the level of the field raised? Give the answer to the second place of decimal.
Solution
Volume of earth dug out = 50 × 40 × 7 m3 = 14000 m3
Let the height of the field rises by h meters
∴ volume of filed (cuboidal) = Volume of earth dugout
⇒ 200 × 150 × h = 14000
⇒ h = 1400/(200 ×150) = 0.47 m
22. A field is in the form of a rectangle of length 18 m and width 15 m. A pit, 7.5 m long, 6 m broad and 0.8 m deep, is dug in a corner of the field and the earth taken out is spread over the remaining area of the field. Find out the extent to which the level of the field has been raised.
Solution
Let the level of the field be risen by h meters volume of the earth taken out from the pit
= 7.5 × 6× 0.8 m3
Area of the field on which the earth taken out is to be spread (X)
= 18 × 15 - 7.5 × 6 = 225 m2
Now, area of the field X× h = volume of the earth taken out from the pit
⇒ 225 × h = 7.5 ×6 × 0.8
⇒ h = 36/225 = 0.16 m = 16 cm
23. A rectangular tank is 80 m long and 25 m broad. Water flows into it through a pipe whose cross-section is 25 cm2 , at the rate of 16 km per hour. How much the level of the water rises in the tank in 45 minutes.
Solution
Let the level of water be risen by h cm.
Then,
Volume of water in the tank = 8000 × 2500 × h cm2
Area of cross - section of the pipe = 25 cm2
Water coming out of the pipe forms a cuboid of base area 25 cm2 and length equal to the distance travelled in 45 minutes with the speed 16 km/hour.
i.e., length = 16000 × 100 × 45/60 cm
∴ Volume of water coming out of pipe in 45 minutes
= 25 × 16000 × 100(45/60)
Now, volume of water in the tank = volume of water coming out of the pipe in 45 minutes
⇒ 8000 × 2500 × h = 16000 × 100 × 45/60 ×25
⇒ h = (16000 ×100 ×45 ×25)/(8000 ×2500 ×60) cm = 1.5 cm
24. Water in a rectangular reservoir having base 80 m by 60 m i s 6.5 m deep. In what time can the water be emptied by a pipe ôf which the cross-section is a square of side 20 cm, if the water runs through the pipe at the rate of 15 km/hr.
Solution
Given that,
Flow of water = 15 km/hr
= 15000 m/hr.
Volume of water coming out of the pipe in one hour
= 20/100 × 20/100 × ± 5000 = 600 m3
Volume of the tank = 80 × 60 × 6.5 = 31200 m3
∴ Time taken to empty the tank = Volume of tank/volume of water coming out of the pipe in one hour
= 31200/600
= 52 hours
25. A village having a population of 4000 requires 150 litres of water per head per day. It has a tank measuring 20 m × 15 m × 6 m. For how many days will the water of this tank last?
Solution
Given that,
Length of the cuboidal tank (l) = 20 m
Breath of the cuboidal tank (b) = 15 m
Height of cuboidal tank (h) = 6 m
Height of the tank = l × b × h = (20 × 15 × 6) m3 = 1800 m3
= 1800000 liters
Water consumed by people of village in one day
= 4000 × 150 litres.
= 600000 litres.
Let water of this tank lasts for n days = capacity of tank
n × 600000 = 1800000
⇒ n = 3
Thus, the water of tank will last for 3 days.
26. A child playing with building blocks, which are of the shape of the cubes, has built a structure as shown in Fig. 18.12 If the edge of each cube is 3 cm, find the volume of the structure built by the child.
= 3 × 3 × 3 cm3 = 27 cm3
Number of cubes in the surface structure = 15
∴ Volume of the structure = 27 × 15 cm3
= 405 cm3

n = 10000/0.9375 = 10666.66
Thus, 10666.66 wooden crates can be stored in go down.
Thickness = 24 cm
Now, each brick is a cuboid with length = 24 cm, Breadth = 12 cm and height = 8 cm
So, the wall requires 167 bricks.