RD Sharma Solutions for Class 9 Chapter 17 Constructions Exercise 17.2

Chapter 17 Constructions RD Sharma Solutions Exercise 17.2 Class 9 Maths

Chapter Name	RD Sharma Chapter 17 Constructions Exercise 17.2
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 17.1 Exercise 17.3
Related Study	NCERT Solutions for Class 10 Maths

Exercise 17.2 Solutions

1. Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC. 

Solution

Steps of construction : 

1. Draw an angle ABO and a Line segment QR
2. With center A and any radius, draw an arc which intersects ∠BAC at E and O
3. With center Q and same radius draw arc which intersect QR at S.
4. With center S and radius equal to DE, draw an arc which intersect previous arc at T
5. Draw a line segment joining Q and T

∴ ∠PQR = ∠BAC

2. Draw an obtuse angle, Bisect it. Measure each of the angles so obtained. 

Solution

 Steps of construction : 

1. Draw angle ABC of 120°
2. With center B and any radius, draw an arc which intersects AB at P and BC at Q 
3. With center P and Q and radius more than 1/2 PQ, draw two arcs, with intersect each other at R. 
4. Join BR 

∴ ∠ABR = ∠RBC = 60°

3. Using your protractor, draw an angle of measure 108° . With this angle as given, draw an angle of 54° . 

Solution

Steps of construction : 

1. Draw an angle ABC of 108°
2. With center B and any radius, draw an arc which intersects AB at P and BC at Q
3. With center P and Q and radius more than 1/2 PQ, draw two arcs, which intersect each other at R. 
4. Join BR 

∴ ∠RBC = 54°

4. Using protractor, draw a right angle. Bisect it to get an angle of measure 45° . 

Solution

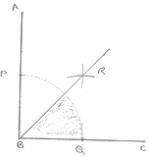
Steps of construction : 

1. Draw an angle ABC of 90°
2. With center B and any radius, draw an arc which intersects AB at P and BC at Q 
3. With center P and Q and radius more than  1/2 PQ, draw two arcs, which intersect each other at R.
4. Join RB 

∴ ∠RBC = 45°

5. Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other. 

Solution

Steps of construction : 

1. Draw two angle DCA and DCB forming Linear pair. 
2. With center C and any radius, draw an arc which intersects AC at P, CD at Q and CB at R. 
3. With center P and Q and any radius draw two arcs which intersect each other at S 
4. Join SC 
5. With center Q and R any radius draw two arcs, which intersect each other at T. 
6. Join TC 

∠SCT = 90° [By using protractor]

6. Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line. 

Solution

Steps of construction : 

1. Draw a pair of vertically opposite angle AOC and DOB 
2. With center O and any radius drawn two arcs which intersect OA at P, Q. OB at S and OD at R. 
3. With center P and Q and radius more than 1/2 PQ, draw two arcs which intersect each other at 7. 
4. Join TO 
5. With center R and S radius more than 1/2 RS, draw two arcs which intersect each other at U. 
6. Join OU. 

∴ TOU is a straight line 

7. Using ruler and compasses only, draw a right angle. 

Solution

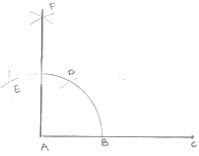
Steps of construction : 

1. Draw a line segment AB 
2. With center A and any radius draw arc which intersect AB at C. 
3. With center C and same radius draw an arc which intersects AB at C.
4. With center D and same radius draw arc which intersect arc in (2) at E.
5. With centers E and C and any radius, draw two arcs which intersect each other at F. 
6. Join FA

∠FAB = 90°

8. Using ruler and compasses only, draw an angle of measure 135° .

Solution

Steps of construction : 

1. Draw a line segment AB and produce BA to point C. 
2. With center A and any radius draw arc which intersect AC at D and AB at E. 
3. With center D and E and radius more than 1/2 DE, draw two arcs which intersect each other at F. 
4. Join FA which intersect the arc in (2) at G. 
5. With centers G and D and radius more than 1/2 GD, draw two arcs which intersect each other a H. 
6. Join HA 

∴ ∠HAB = 135°

9. Using a protractor, draw an angle of measure 72° . With this angle as given, draw angles of measure 36° and 54°.

Solution

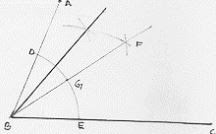
Steps of construction : 

1. Draw an angle ABC of 72° with the help of protractor. 
2. With center B and any radius, draw an arc which intersect AB at D and BC at E. 
3. With center D and E and radius more than 1/2 DE, draw two arcs which intersect each other at F. 
4. Join FB which intersect the arc in (2) at G. 
5. With centers D and G and radius more than 1/2 DE, draw two arcs which intersect each other at F. 
6. With centers D and G and radius more than  draw two arcs which intersect each other at H. 
7. Join HB 

∴ ∠HBC = 54°

∠FBC = 36°

10. Construct the following angles at the initial point of a given ray and justify the construction : 

(i) 45°

(ii) 90°

Solution

Steps of construction : 

1. Draw a line segment AB and produce BA to point C. 
2. With center A and any radius drawn an arc which intersect AC at D and AB at E. 
3. With center D and E and radius more than 1/2 DE, draw arcs cutting each other at F. 
4. Join FA which intersect arc in (2) at G. 
5. With centers G and E and radius more than  1/2 GE, draw arcs cutting each other at H. 
6. Join HA 

∴ ∠HAB = 45°

(ii) 

Steps of construction : 

1. Draw a line segment AB. 
2. With center A and any radius draw in arc which intersect AB at C. 
3. With center C and same radius draw an arc which intersects previous arc at D. 
4. With centers D same radius draw an arc which intersects are in (2) at E. 
5. With centers E and D same radius more than 1/2 ED draw an arc cutting each other at F. 
6. Join FA 

∠FAB = 90°

11. Construct the angles of the following measurements :

(i) 30°

(ii) 75°

(iii) 105°

(iv) 135°

(v) 15°

(vi) 45°/2
Solution 

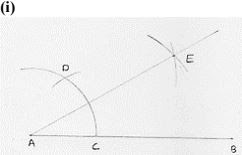
Steps of construction :

1. Draw a line segment AB. 
2. With center A and any radius, draw an arc which intersect AB at C. 
3. With center C and same radius, draw an arc which intersects previous arc at D. 
4. With centers D and C and radius more than 1/2 DC, draw arcs intersecting each other at E. 
5. Join EA

∴ ∠EAB = 30°

(ii) 

Steps of construction : 

1. Draw a line segment AB. 
2. With center A any radius, draw an arc which intersect AB at C. 
3. With center C and same radius, draw an arc which intersects previous arc at D. 
4. With center D and same radius, draw an arc which intersects are in (2) at E. 
5. With centers E and D and radius more than  1/2 ED, draw arcs intersecting each other at F. 
6. Join FA which intersects arc in (2) at G 
7. With centers G and D, and radius more than 1/2 GD, draw arcs intersecting each other at H. 
8. Join HA

∴ ∠HAB = 75°

(iii) 

Steps of construction : 

1. 1Draw a line segment AB. 
2. With center A and any radius, draw an arc intersect AB at C. 
3. With center C and same radius, draw an arc which intersects previous arc at D. 
4. With center D and same radius, draw an arc which interest are in (2) at E. 
5. With centers E and D and radius more than 1/2 ED, draw arcs intersecting each other at F. 
6. Join FA which intersects arc in (2) at E. 
7. With centers E and G, and radius more than half of EG, draw arcs intersecting each other at H. 
8. Join HA 

∠HAB = 105°

(iv) 

Steps of construction : 

1. Draw a line segment AB and produce BA to point C
2. With center A and any radius, draw an arc which intersect AC to D and AB at E. 
3. With center D and E and radius more than half of DE, draw two arcs which intersects each other at F. 
4. Join FA which intersect the arc in (2) at G. 
5. With center G and D radius more than 1/2 GD, draw two arcs which intersect each other at H. 
6. Join HA 

∠HAB = 135°

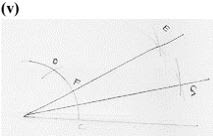
Steps of construction : 

1. Draw a line segment AB
2. With center A and any radius, draw an arc which intersects previous arc at C . 
3. With center C and same radius, draw an arc which intersect previous arc at D .
4. With center D and C radius more than half of DC draw arcs intersecting each other at E.
5. Join EA which intersects arc in (2) at F. 
6. With centers F and C and radius more than 1/2 FC, draw arcs intersecting each other.
7. Join GA 

∴ ∠GAB = 15°

(vi) 

Steps of construction : 

1. Draw a line segment AB 
2. With center A and any radius, draw an arc which intersects AB at C .
3. With center C and same radius, draw an arc which intersect previous arc at D. 
4. With center D and same radius, draw an arc which intersects arc in (2) at E. 
5. With center E and D and radius more than half of ED, draw arcs intersecting each
6. other at F.
7. Join FA which intersects arc in (2) at G. 
8. With center G and C and radius more than half of GC, draw arcs intersecting each other at H. 
9. Join HA which intersects arc in (2) at 1. 
10. With centers I and C and radius more than half of IC, draw arcs intersecting each other. 
11. Join JA 

∴ ∠JAB = 45°/2