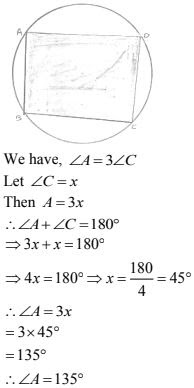RD Sharma Solutions for Class 9 Chapter 16 Circles Exercise 16.5

Chapter 16 Circles RD Sharma Solutions Exercise 16.5 Class 9 Maths

Chapter Name	RD Sharma Chapter 16 Circles Exercise 16.5
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 16.1 Exercise 16.2 Exercise 16.3 Exercise 16.4
Related Study	NCERT Solutions for Class 10 Maths

Exercise 16.5 Solutions

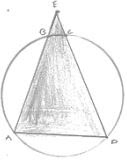
1. In the below fig. ΔABC is an equilateral triangle. Find in ∠BEC. 

Solution

Since, ΔABC is an equilateral triangles 
Then, ∠BAC = 60° 
∴ ∠BAC + ∠BEC = 180° [Opposite angles of a quadrilaterals]
⇒ 60° + ∠BEC = 180°
⇒ ∠BEC = 180° - 60°
⇒ ∠BEC = 180°

2. In the below fig. ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35° . Find m ∠QSR and m ∠QTR. 

Solution

3. In the below fig., O is the centre of the circle. If ∠BOD = 160°, find the values of x and y. 

Solution

Given that O is the centre of the circle 
We have, ∠BOD = 160° 
By degree measure theorem 
∠BOD = 2∠BCD
⇒ 160° = 2 × x 
⇒ x = 160/2 = 80°
∴ ∠BAD + ∠BCD = 180° [Opposite angles of cyclic quadrilaterals]
⇒ y + x = 180°
⇒ y + 80° = 180°
⇒ y = 180° - 80° = 100°

4. In the below fig. ABCD is a cyclic quadrilateral. It ∠BCD = 100° and ∠ABD = 70°, find ∠ADB. 

Solution

5. If ABCD is a cyclic quadrilateral in which AD || BC (Fig. below). Prove that ∠B = ∠C. 

Solution

Since ABCD is a cyclic quadrilateral with AD || BC.  
Then ∠A + ∠C = 180° ... (1)  [Opposite angles of cyclic quadrilaterals]

And, ∠A + ∠B = 180° ...(2) [Co interior angles]
Compare (1) and (2) equations ∠B = ∠C 

6. In the below fig. O is the centre of the circle. Find ∠CBD. 

Solution 

Given that ∠BOC = 100°
By degree measure theorem 

7. In the below fig. AB and CD are diameters of a circle with centre O. if ∠OBD = 50°, find ∠AOC. 

Solution

Given that, 

∠OBD = 50°
Since, AB and CD are the diameter of circle then O is the center of the circle 

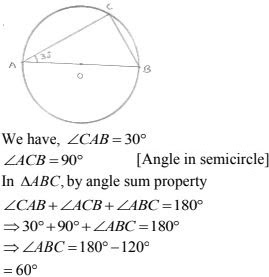
8. On a semi - circle with AB as diameter, a point C is a taken, so that m (∠CAB) = 30°. Find m (∠ACB) and m(∠ABC). 

Solution

9. In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.

Solution

Given that ∠B = 70° = 70°
Since ABCD is a cyclic quadrilaterals 

10. In a quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A. 

Solution

11. In the below fig. O is the centre of the circle and ∠DAB = 50°. Calculate the values of x and y. 

Solution

We have ∠DAB = 50°

By degree measure theorem 

∠BOD = 2∠BAD 
⇒ x = 2 × 50 = 100°

Since, ABCD is a cyclic quadrilateral 
Then ∠A + ∠C = 180 °
⇒ 50 + y = 180°
⇒ y = 180° - 50° = 130°

12. In the below fig. in ∠BAC = 60° and ∠BCA = 20° , find ∠ADC. 

Solution

By using angle sum property in ΔABC
∠B = 180° - (60° + 20°) = 100°

In cyclic quadrilaterals ABCD, we have : 

∠B + ∠D = 180° 
∠D = 180° - 100° = 80°

13. In the below fig. if ABC is an equilateral triangle. Find ∠BDC and ∠BEC. 

Solution 

Since ΔABC is an equilateral triangle 

Then, ∠BAC = 60°
∴ ∠BDC = ∠BAC = 60°  [Angles in same segment]
Since, quadrilaterals ABEC is a cyclic quadrilaterals 

Then ∠BAC + ∠BEC = 180°

⇒ 60° + ∠BEC = 180°

⇒ ∠BEC = 180° - 60° = 120°

14. In the below fig. O is the centre of the circle, if ∠CEA = 30°, find the values of x, y and z. 

Solution

We have ∠AEC = 30° 
Since, quadrilateral ABCE is a cyclic quadrilaterals 

Then, ∠ABC + ∠AEC = 180°

x + 30° = 180°

⇒ x = 180 - 30 = 150°

By degree measure theorem 

∠AOC = 2∠AEC 

⇒ y = 2× 30° = 60°
⇒ ∴ ∠ADC = ∠AEC  [Angles in same segment]

15. In the below fig. ∠BAD = 78° , ∠DCF = x° and ∠DEF = y° . Find the values of x, and y. 

Solution

We have, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°

Since, ABCD is a cyclic quadrilateral 

Then, ∠BAD + ∠BCD = 180°
⇒ 78° + ∠BCD = 180° 

⇒ ∠BCD = 180° - 78° = 102° 

Now, ∠BCD + ∠DCF = 180° [Linear pair of angles]

⇒ 102° = x - 180°

⇒ x = 180° - 102° = 78° 

Since, DCEF is a cyclic quadrilateral 

Then, x + y = 180°

⇒ 78° + y = 180° 

⇒ y = 180° - 78° = 102° 

∴ y = 102° 

16. In a cyclic quadrilateral ABCD, if ∠A - ∠C = 60° , prove that the smaller of two is 60° . 

Solution

17. In the below fig. ABCD is a cyclic quadrilateral. Find the value of x. 

Solution

18. ABCD is a quadrilateral in which : 

(i) BC || AD, ∠ADC = 110° and ∠BAC = 50° . Find ∠DAC.

(ii) ∠DBC = 80° and ∠BAC = 40°, find ∠BCD.

(iii) ∠BCD = 100° and ∠ABD = 70°, find ∠ADB. 

Solution

(i)

Since, ABCD is a cyclic quadrilateral 

Then, ∠ABC + 110° = 180°

⇒ ∠ABC + 110° = 180°
⇒ ∠ABC = 180° - 110° = 70°
Since AD || BC
Then, ∠DAB + ∠ABC = 180°  [Co - interior angle]
⇒ ∠DAC + 50° + 70° = 180°
⇒ ∠DAC = 180° - 120° = 60°

(ii) ∠BAC = ∠BDC = 40°  [Angle in same segment]
In ΔBDC, by angle sum property 

∠DBC + ∠BCD + ∠BDC = 180° 
⇒ 80° + ∠BCD + 40° = 180°
⇒ ∠BCD = 180° - 40° - 80°

⇒ ∠BCD = 60°

(iii) Given that ABCD is a cyclic quadrilaterals 
Ten ∠BAD + ∠BCD = 180°
⇒∠BAD + 100° = 180°

⇒ ∠BAD  = 180° - 100°
⇒ ∠BAD = 80° 

In ΔABD, by angle sum property 

∠ABD + ∠ADB + ∠BAD = 180°

⇒ 70° + ∠ADB + 80° = 180°

⇒ ∠ADB = 180° - 150°

⇒ ∠ADB = 30°

19. Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent. 

Solution

Let ABCD be a cyclic quadrilateral, and let O be the center of the corresponding circle.

Then, each side of the equilateral ABCD is a chord of the circle and the perpendicular

bisector of a chord always passes through the center of the circle.

So, right bisectors of the sides of quadrilaterals ABCD, will pass through the circle O of the

corresponding circle

20. Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals. 

Solution

Let O be the circle circumscribing the cycle rectangle ABCD. Since ∠ABC = 90° and AC is a chord of the circle, so AC is a diameter of a circle. Similarly BD is a diameter 

Hence, point of intersection of AC and BD is the center of the circle 

21. Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals. 

Solution

Let ABCD be a rhombus such that its diagonals AC and BD interest at O

Since, the diagonals of a rhombus intersect at right angle
∴ ∠ACB = ∠BOC = ∠COD = ∠DOA = 90°
Now, ∠AOB = 90°

⇒ circle described on BC, AD and CD as diameter pass through O.  

22. If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.

Solution

Given ABCD is a cyclic quadrilateral in which AB = DC

To prove : AC = BD

Proof : In ΔPAB and ΔPDC 

Given that AB = DC

∠BAD  = ∠CDP  [Angles in the same segment]
∠PBA = ∠PCD  [Angles in same segment]

Then ΔPAB = ΔPDC  ...(1) [c.p.c.t]
PC = PB  ...(2) [c.p.c.t]
Add equation (1) and (2) 
PA + PC = PD + PB 
⇒ AC = BD

23. ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that 

(i) AD || BC 
(ii) EB = EC

Solution

Given ABCD is a cyclic quadrilateral in which EA = ED

To prove:

(i) AD || BC

(ii) EB = EC
Proof:

(i) Since EA = ED  
Then ∠EAD = ∠EDA  [Opposite angles to equal sides]

Since, ABCD is a cyclic quadrilaterals 

Then, ∠ABC + ∠ADC = 180°
But ∠ABC + ∠EBC = 180°  [Linear pair of angles] 
Then ∠ADC = ∠EBC ...(2)
Compare equation (1) and (2)
∠EAD = ∠CBA  ...(3)
Since, corresponding angle are equal 

Then BC || AD 

(ii) From equation (2) 
∠EAD = ∠CBA  ...(3)
Since, corresponding angle are equal 

Then BC || AD 
(ii) From equation (2) 
∠EAD = ∠EBC ...(3)
Similarly ∠EDA = ∠ECB ...(4) 
Compare equation (1), (3) and (4) ∠EBC  = ∠ECD 

⇒ EB = EC  (Opposite angles to equal sides) 

24. Circles are described on the sides of a triangle as diameters. Prove that the circles on any

two sides intersect each other on the third side (or third side produced).

Solution

Since AB is a diameter 

Then ∠ADB = 90°  ...(1) [Angle in semicircle]

Since AC is a diameter 

Then ∠ADC = 90°  ...(2) [Angle in semicircle]
Add equation (1) and (2) 
∠ADB + ∠ADC = 90° + 90°
⇒ ∠BDC = 180°
Then, BDC is a line 

Hence, the circles on any two sides intersect each other on the third side 

25. Prove that the angle in a segment shorter than a semicircle is greater than a right angle. 

Solution

27. ABCD is a cyclic trapezium with AD || BC. If ∠B = 70° , determine other three angles of the trapezium. 

Solution

Given that 

ABCD is a cyclic trapezium with AD || BC and ∠B = 70°

Since, ABCD is a quadrilateral 

Then ∠B + ∠D = 180°

28. Prove that the line segment joining the mid - point of the hypotenuse of a right triangle to its opposite vertex is half of the hypotenuse. 

Solution 

Let ΔABC be a right angle triangle at angle B. 

Let P be the midpoint of hypotenuse AC. 

Draw a circle with center P and AC as a diameter 

Since, ∠ABC = 90° , therefore the circle passes through B 
∴ BP = radius 

Also AD = CP = Radius 

∴ AP = BP = CP

Hence, BP = 1/2 AC. 

29. In Fig. below, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD .

Solution

Since angles in the same segment of a circle are equal 

∴ ∠CAD = ∠DBC = 65°

∴ ∠DAB = ∠CAD + ∠BAC = 55° + 45° = 100°

But, ∠DAB + ∠BCD = 180°  [Opposite angles of a cyclic]

∴ ∠BCD = 180° - 100° = 80°
∴ ∠BCD = 80°