RD Sharma Solutions for Class 9 Chapter 15 Areas of Parallelograms and Triangles Exercise 15.3

Chapter 15 Areas of Parallelograms and Triangles RD Sharma Solutions Exercise 15.3 Class 9 Maths

Chapter Name	RD Sharma Chapter 15 Areas of Parallelograms and Triangles Exercise 15.3
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 15.1 Exercise 15.2
Related Study	NCERT Solutions for Class 10 Maths

Exercise 15.3 Solutions

1. In the below figure, compute the area of  quadrilateral ABCD.

Solution

Given that,

DC = 17 cm 

AD = 9cm and BC = 8cm 

In ΔBCD we have 

2. In the below figure, PQRS is a square and T and U are respectively, the mid - points of PS and QR. Find the area of ΔOTS if PQ = 8 cm. 

Solution

From the figure 

T and U are the midpoints of PS and QR respectively. 
∴ TU || PQ 
⇒ TO || PQ 
Thus, in ΔPQS, T is the midpoint of PS and TO || PQ 

3. Compute the area of trapezium PQRS is Fig. below. 

Solution

We have

4. In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of ΔAOB.

Solution

Since, the midpoint of the hypotenuse of a right triangle is equidistant from the vertices 
∴ CA = CB = OC 
⇒ CA = CB = 6.5 cm 

⇒ AB = 13 cm 

In a right angle triangle OAB, we have

5. In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,

and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.

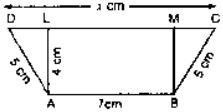
Solution 

6. In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If OE = 2√5, find the area of the rectangle. 

Solution

Given OD = 10 cm and OE = 2√5 cm 

By using Pythagoras theorem 

7. In the below fig. ABCD is a trapezium in which AB || DC. Prove that ar(ΔAOD) = ar(ΔBOC). 

Solution

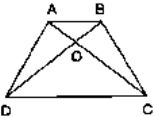
Given : ABCD is a trapezium with AB || DC
To prove : ar(ΔAOD) = ar (BOC) 
Proof : 

Since ΔADC and ΔBDC are on the same base DC and between same parallels AB and DC 

8. In the given below fig. ABCD, ABFE and CDEF are parallelograms. Prove that ar(ΔADE) = ar(ΔBCF) .

Solution

Given that, 

ABCD is a parallelogram ⇒ AD = BC 
CDEF  is a parallelogram ⇒ DE = CF 
ABFE is a parallelogram ⇒ AE = BF 

Thus, in Δs ADE and BCF, we have 

AD = BC, DE = CF and AE = BF 

So, by SSS criterion of congruence, we have 
ΔADE ≅ ΔABCF 

∴ ar(ΔADE) = ar(BCF) 

9. Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that: 

ar(∆APB) × ar(∆CPD) = ar(∆APD) × ar (∆BPC)

Solution

10. In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is bisected by AB at O, show that ar (ΔABC) = ar (ΔABD) 

Solution

Given that CD is bisected at O by AB 

To prove : ar(ΔABC) = ar(ΔABD) 
Construction : Draw CP ⊥ AB and DQ ⊥ AB 

Proof :

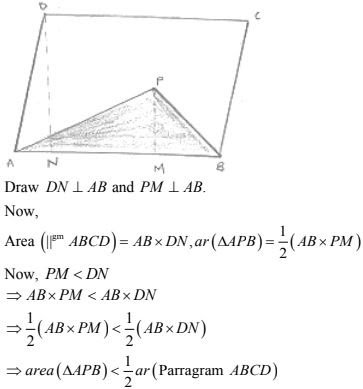
11. If P is any point in the interior of a parallelogram ABCD, then prove that area of the triangle APB is less than half the area of parallelogram. 

Solution

12. If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in area. If G is the mid - point of median AD, prove that ar(ΔBGC) = 2 ar(ΔAGC). 

Solution

13. A point D is taken on the side BC of a ΔABC such that BD = 2DC.  Prove that ar(ΔABD) = 2 ar(ΔADC).

Solution

Given that, 

In ΔABC, BD = 2DC
To prove : ar(ΔABD) = 2ar (ΔADC) 
Construction : Take a point E on BD such that BE = ED 
Proof : Since, BE = ED and BD = 2DC
Then, BE = ED = DC 

We know that median of Δ^le  divides it into equal Δ^les .
∴ In ΔABD,  AE is a median 

Then, area (ΔABD) = 2ar(ΔAED) ...(i) 

In ΔAEC, AD is a median 

Then area (ΔAED) = area (ΔADC) ...(ii) 
Compare equation (i) and (ii) 
Area (ΔABD) = 2ar(ΔADC). 

14. ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, Prove that: 

(i) ar (ΔADO) = ar(ΔCDO) 
(ii) ar(ΔABP) = ar(ΔCBP) 

Solution

Given that ABCD is a parallelogram 

To prove : (i) ar(ΔADO) = ar(ΔCDO) 
(ii) ar(ΔABP) = ar(ΔCBP) 
Proof: We know that, diagonals of a parallelogram bisect each other 

∴ AO = OC and BO = OD

(i) In ΔDAC, since DO is a median 

Then area (ΔADO) = area (ΔCDO) 

(ii) In ΔBAC, Since BO is a median 

Then; area (ΔBAO) = area (ΔBCO)  ...(1)
In a ΔPAC, Since PO is a median 

Then, area (ΔPAO) = area (ΔPCO)  ...(2)

Subtract equation (2) from equation (1) 

⇒ area(ΔBAO) - ar(ΔPAO) = ar(ΔBCO) - area(ΔPCO) 
⇒ Area (ΔABP) = Area of ΔCBP

15.ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F. 

(i) Prove that ar(ΔADF) = ar(ΔECF)
(ii) If the area of ΔDFB = 3 cm², find the area of ||^gm  ABCD.

Solution

In triangles ADF and ECF, we have 

∠ADF = ∠ECF  [Alternative interior angles, Since AD || BE]
AD = EC  [Since AD = BC = CE]
And ∠DFA  = ∠CFA  [vertically opposite angles]

So, by AAS congruence criterion, we have 

ΔADF ≅ ΔECF 

⇒ area (ΔADF) = area (ΔECF) and DF = CF. 

Now, DF = CF

⇒ BF is a median in ΔBCD

⇒ area (ΔBCD) = 2ar(ΔBDF) 
⇒ area (ΔBCD) = 2×3 cm²  = 6cm² 

Hence, ar(||^gm ABCD) = 2ar(ΔBCD) = 2 × 6 cm²  = 12cm² 

16. ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar(ΔPOA) = ar(ΔQOC). 

Solution

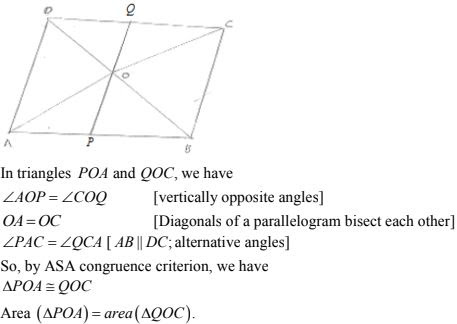
17. ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram ABCD. 

Solution

18. In a ΔABC, P and Q are respectively the mid - points of AB and BC and R is the mid - point of AP. Prove that : 

(i) ar(ΔPBQ) = ar (ΔARC)
(ii) ar (ΔPRQ) = 1/2 ar(ΔARC) 
(iii) ar(ΔRQC) = 3/8 ar (ΔABC). 

Solution

19. ABCD is a parallelogram, G is the point on AB such that AG = 2 GB, E is a point of DC such that CE = 2DE and F is the point of BC such that BF  = 2FC. Prove that : 
(i) ar(ADEG) = ar(GBCE) 
(ii) ar(ΔEGB) = 1/6 ar(ABCD) 
(iii) ar(ΔEFC) = 1/2 ar(ΔEBF) 
(iv) ar(ΔEBG) = ar(ΔEFC) 
(v) Find what portion of the area of parallelogram is the area of ΔEFG. 

Solution

20. In Fig. below, CD || AE and CY || BA.

(i) Name a triangle equal in area of ΔCBX 

(ii) Prove that ar (ΔZDE) = ar(ΔCZA) 
(iii) Prove that ar(BCZY) = ar(ΔEDZ) 

Solution

Since, ΔBCA and ΔBYA are on the same base BA and between same parallels BA and CY 

Then area (ΔBCA) = ar(ΔBYA) 
⇒ ar(ΔCBX) + ar(ΔBXA) = ar(ΔBXA) + ar(ΔAXY) 
⇒ ar(ΔCBX) = ar(ΔAXY) ...(1)
Since, ΔACE and ΔADE are on the same base AE and between same parallels CD and AE 
Then, ar(ΔACE)  = ar(ΔADE) 
⇒ ar(ΔCLA) + ar(ΔAZE) = ar(ΔAZE) + ar(ΔDZE)

⇒ ar(ΔCZA) = (ΔDZE) ...(2)
Since ΔCBY and ΔCAY are on the same base CY and between same parallels 
BA and CY 

Then ar(ΔCBY) = ar(ΔCAY) 
Adding ar(ΔCYG) on both sides, we get 

⇒ ar(ΔCBX) + ar(ΔCYZ) = ar(ΔCAY) + ar(ΔCYZ) 
⇒  ar(BCZX) = ar(ΔCZA) ...(3)
Compare equation (2) and (3)
ar(BCZY) = ar(ΔDZE) 

21. In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove that ar(ΔPQE) = ar(ΔCFD).

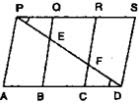
Solution

Given that PSDA is a parallelogram 

Since, AP || BQ || CR || DS and AD|| PS 
∴ PQ = CD ...(i) 
In ΔBED, C is the midpoint of BD and CF || BE 

∴ F is the midpoint of ED 

⇒ EF = PE 

Similarly 

EF = PE

∴ PE = FD ...(2) 
In ΔSPQE and CFD, we have 

PE = FD  [Alternative angles]
∠EDQ = ∠FDC, 
And PQ = CD 

So, by SAS congruence criterion, we have ΔPQE ≅ ΔDCF. 

12. In the below fig. ABCD is a trapezium in which AB || DC and DC = 40 cm and AB = 60 cm. If  X and Y are respectively, the mid - points of AD and BC, prove that : 

(i) XY = 50 cm 

(ii) DCXY is a trapezium 

(iii) ar(trap. DCYX) = 9/11 ar(trap. XYBA) 

Solution

23. In Fig. below, ABC and BDE are two equilateral triangles such that D is the mid - point of BC. AE intersects BC in F. Prove that 

(i) ar(ΔBDE) = 1/4 ar(ΔABC) 
(ii) ar(ΔBDE) = 1/2 ar(ΔBAE) 
(iii) ar(ΔBEF) = ar(ΔAFD). 

(iv) ar(ΔABC) = ar(ΔBEC) 
(v) ar(ΔFED) = 1/8 ar(ΔAFC) 
(vi) ar(ΔBFE) = 2ar(ΔEFD) 

Solution

Given that, 

ABC and BDE are two equilateral triangles. 

Let AB = BC = CA = x. Then BD = x/2 = DE = BE

(ii) It is given that triangles ABC and BED are equilateral triangles 
∠ACB = ∠DBE = 60°
⇒ BE || AC (Since alternative angles are equal)
Triangles BAF and BEC are on the same base 

BE and between the same parallel BE and AC 

∴ ar(ΔBAE) = area(ΔBEC) 
⇒ ar(ΔBAE) = 2ar(ΔBDE) 
[∵ED is a median of ΔEBC; ar(ΔBEC) = 2ar(ΔBDE)] 
⇒ area(ΔBDE) = 1/2 ar(ΔBAE) 

(iii) Since ΔABC and ΔBDE are equilateral triangles 

∴ ∠ABC = 60° and ∠BDE = 60°
∠ ABC = ∠BDE 

⇒ AB || DE (Since alternative angles are equal)
Triangles BED and AED are on the same base ED and between the same parallels AB and DE. 

∴ ar(ΔBED) = area(ΔAED) 
⇒ ar(ΔBED) - area (ΔEFD) = area (AED) - area (ΔEFD) 
⇒ ar(BEF) = ar(ΔAFD). 

(iv) Since ED is the median of ΔBEC

∴ area(ΔBEC) = 2ar(ΔBDE) 
⇒ ar(ΔBEC) = 2 × 1/4 ar(ΔABC) [from (i)] 

⇒ ar(ΔBEC) = 1/2 area(ΔABC) 
⇒ area(ΔABC) = 2area (ΔBEC) 

(v) Let h be height of vertex E, corresponding to the side BD on triangle BDE 

Let H be the height of the vertex A corresponding to the side BC in triangle ABC 
From part (i) 

24. D is the mid - point of side BC of ΔABC and E is the mid - point of BD. If O is the mid - point of AE, prove that ar(ΔBOE) = 1/8 ar(ΔABC). 

Solution

25. In the below fig. X and Y are the mid - points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar(ΔABP) = ar(ΔACQ). 

Solution

Since x and y are the midpoint AC and AB respectively

∴ XY || BC 

Clearly, triangles BYC and BXC are on the same base BC and between the same parallels XY and BC 

We observe that the quadrilateral XYAP and XY AQ are on the same base XY and between the same parallel XY and PQ . 

∴ area (quad XY AP) = ar(quad XYPA) 
Adding (i) and (ii) , we get 

ar(ΔBXY) + ar(quadXYAP) = ar(CXY) + ar(quad XYQA) 
⇒ ar(ΔABP) = ar(ΔACQ) 

26. In the below fig. ABCD and AEFD are two parallelograms. Prove that 

(i) PE = FQ 
(ii) ar(ΔAPE) : ar(ΔPFA) = ar(ΔQFD) :  ar(ΔPFD) 
(iii) ar(ΔPEA) = ar(ΔQFD) 

Solution

Given that, ABCD and AEFD are two parallelograms 

To prove : (i) PE = FQ 

(ii) Since, ΔPEA and ΔQFD stand on the same base PE and FQ lie between the same parallels EQ and AD 

27. In the below figure, ABCD is parallelogram. O is any point on AC. PQ || AB and LM || AD. Prove that ar(||^gm DLOP) = ar(||^gm BMOQ)

Solution

Since, a diagonal of a parallelogram divides it into two triangles of equal area 

∴ area (ΔADC) = area(ΔABC) 

Since, AO and OC are diagonals of parallelograms AMOP and OQCL respectively.  

28. In a ΔABC, if L and M are points on AB and AC respectively such that LM || BC. Prove that : 

(i) ar(ΔLCM) = ar(ΔLBM) 
(ii) ar(ΔLBC) = ar(ΔMBC) 
(iii) ar(ΔABM) = ar(ΔACL) 
(iv) ar(ΔLOB) = ar(ΔMOC) 

Solution

(i) Clearly Triangles LMB and LMC are on the same base LM and between the same parallels LM and BC. 
∴ ar(ΔLMB) = ar(ΔLMC) ...(i) 

(ii) We observe that triangles LBC and MBC area on the same base BC and between the same parallels LM and BC 

∴ arc ΔLBC = ar(ΔMBC) ...(ii) 

(iii) We have 

ar(ΔLMB) = ar(ΔLMC) [from (i)]
⇒ ar(ΔALM) + ar(ΔLMB) = ar(ΔALM) + ar(ΔLMC) 
⇒ ar(ΔABM) = ar(ΔACL) 

(iv) We have 

ar(ΔCBC) = ar(ΔMBC)  ∴ [from (i)] 
⇒ ar(ΔLBC) = ar(ΔBOC) = ar(ΔMBC) - ar(ΔBOC)

⇒ ar(ΔLOB) = ar(ΔMOC) 

29. In the below fig. D and E are two points on BC such that BD = DE = EC. Show that ar(ΔABD) = ar(ΔADE) = ar(ΔAEC). 

Solution

Draw a line through A parallel to BC 

Given that, BD = DE = EC

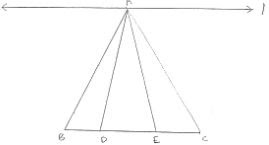
We observe that the triangles ABD and AEC are on the equal bases and between the same parallels C and BC. Therefore, Their areas are equal. 

Hence, ar(ΔABD) = ar(ΔADE) = ar(ΔACDE) 

30. If below fig. ABC is a right triangle right angled at A, BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. 

Show that: 

(i) ΔMBC ≅ ΔABD 

(ii) ar(BYXD) = 2 ar(ΔMBC)

(iii) ar(BYXD) = ar(ΔABMN) 

(iv) ΔFCB ≅ ΔACE

(v) ar(CYXE) = 2 ar(ΔFCB)

(vi) ar(CYXE) =  ar(ACFG) 

(vii) ar (BCED) = ar(ABMN) + ar(ACFG)

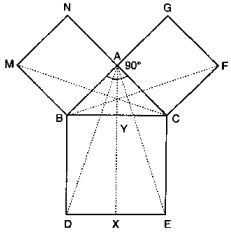
Solution

(i) In ΔMBC and ΔABD, we have 

MB = AB

BC = BD

And ∠MBC = ∠ABD

[∵ ∠MBC and ∠ABC are obtained by adding ∠ABC to a right angle]

So, by SAS congruence criterion, We have

ΔMBC ≅ ΔABD

⇒ ar(ΔMBC) = ar(ΔABD) ...(1) 

(ii) Clearly, ΔABC and BYXD are on the same base BD and between the same parallels AX and BD

 

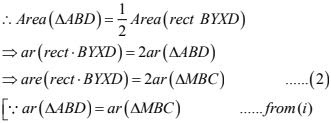
(iii) Since triangle M. BC and square MBAN are on the same Base MB and between the same parallels MB and NC

∴ 2ar(ΔMBC) = ar(ΔMBAN) ...(3) 
From (2) and (3) we have 

ar(sq. MBAN) = ar(rect BYXD).

(iv) In triangles FCB and ACE we have 

FC = AC

CB = CF

And ∠FCB = ∠ACE

[∵ ∠FCB and ∠ACE are obtained by adding ∠ACB to a right angle]

So, by SAS congruence criterion, we have 

ΔFCB ≅ ΔACE 

(v) We have 

ΔFCB ≅ ΔACE
⇒ ar(ΔFCB) = ar(ΔECA)

Clearly, ΔACE and rectangle CYXE are on the same base CE and between the same parallels CE and AX 

∴ 2ar (ΔACE) = ar(CYXE) 

(vi) Clearly, ΔFCB and rectangle FCAG are on the same base FC and between the same parallels FC and BG

∴ 2ar(ΔFCB) = ar(FCAG)

From (4) and (5), we get 

Area (CYXE) = ar(ACFG)

(vii) Applying Pythagoras theorem in ΔACB, we have