RD Sharma Solutions for Class 9 Chapter 14 Quadrilaterals Exercise 14.4

Chapter 14 Quadrilaterals RD Sharma Solutions Exercise 14.4 Class 9 Maths

Chapter Name	RD Sharma Chapter 14 Quadrilaterals Exercise 14.4
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 14.1 Exercise 14.2 Exercise 14.3
Related Study	NCERT Solutions for Class 10 Maths

Exercise 14.4 Solutions

1. In a ΔABC, D, E and F are, respectively, the mid - point of BC, CA and AB. If the length of side AB, BC and CA are 7cm, 8cm and 9cm, respectively, find the perimeter of ΔDEF. 

Solution

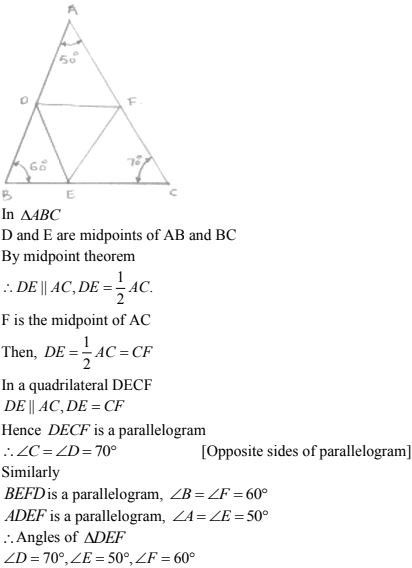
2. In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70° . Find the measure of the angles of the triangle formed by joining the mid - points of the sides of this triangle .

Solution

3. In a triangle, P, Q and R are the mid - points of sides BC, CA and AB respectively. If AC  = 21cm, BC = 29cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ. 

Solution

4. In a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a parallelogram. 

Solution

In a quadrilateral ABXC, we have 

AD = DX  [Given]
BD = DC  [Given]

So, diagonals AX and BC bisect each other 

∴ ABXC is a parallelogram 

5. In a ΔABC, E and F are the mid - points of AC and AB respectively. The altitude AP to BC intersects FE at Q. Prove that AQ = QP.

Solution

In ΔABC 

E and F are midpoints of AB and AC 

∴ EF || FE, 1/2 BC = FE  [∵ By mid - point theorem]

In ΔABP,

F is the midpoint of AB and FQ || BP  [∵ EF || BC]
∴ Q is the midpoint of AP  [By converse of midpoint theorem]

Hence, AQ = QP 

6. In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid - point of BC,  prove that ML = NL. 

Solution

7. In Fig. below, triangle ABC is right  - angled at B. Given that AB = 9cm, AC = 15 cm and D, E are the mid - points of the sides AB and AC respectively, calculate

(i) The length of BC 

(ii) The area of ΔADE. 

Solution

8. In fig. below, M, N and P are the mid - points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, calculate BC, AB and AC. 

Solution

9. ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P, Q and R . Prove that the perimeter of ΔPQR is double the perimeter of ΔABC.

Solution

10. In Fig. below, BE ⊥ AC. AD is any line from A to BC intersecting BE in H. P, Q and R are respectively the mid - points of AH, AB and BC. Prove that ∠PQR = 90°  .

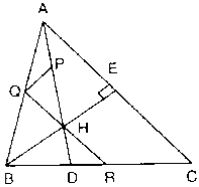
Solution

11. In Fig. below, AB = AC and CP || BA and AP is the bisector of exterior ∠CAD of ΔABC.

Prove that:

(i) ∠PAC = ∠BCA

(ii) ABCP is a parallelogram .

Solution

12. ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the mid-points of the sides, in order, is a rectangle. 

Solution

Given,

A kite ABCD having AB = AD and BC = CD. P,Q,R,S are the midpoint of sides AB, BC, CD and DA respectively PQ, QR, RS and spare joined 

To prove : 

PQRS is a rectangle 

Proof: 

In ΔABC, P and Q are the midpoints of AB and BC respectively. 

∴ PQ || AC and PQ = 1/2 AC ...(i) 
In ΔADC, R and S are the midpoint of CD and AD respectively .

∴ RS || AC and RS = 1/2 AC ...(ii) 
From (i) and (ii),  we have 

PQ || RS and PQ = RS 

Thus, in quadrilateral PQRS, a pair of opposite sides are equal and parallel. So PQRS is a parallelogram. Now, we shall prove that one angle of parallelogram PQRS it is a right angle 

Since AB = AD 

13. Let ABC be an isosceles triangle in which AB = AC. If D, E, F be the mid - points of the sides BC, CA and AB respectively. Show that the segment AD and EF bisect each other at right angles. 

Solution

14. ABC is a triangle. D is a point on AB such that AD = 1/4 AB and E is a point on AC such that AE = 1/4 AC. Prove that DE = 1/4 BC.

Solution

Let P and Q be the midpoints of AB and AC respectively. 

Then PQ || BC such that 

PQ = 1/2 BC ...(i) 
In ΔAPQ, D and E are the midpoint of AP and AQ are respectively 

15. In below Fig, ABCD is a parallelogram in which P is the mid - point of DC and q is a point on AC such that CQ = 1/4 AC. If PQ produced meets BC at R, prove that R is a mid - point of BC. 

Solution

16. In the below Fig, ABCD and PQRC are rectangles and Q is the mid - point of AC. Prove that 
(i) DP = PC 
(ii) PR = 1/2 AC

Solution

(i) In ΔADC, Q is the midpoint of AC such that 

PQ || AD 

∴ P is the midpoint of DC 

⇒ DP = DC  [Using converse of midpoint theorem]
(ii) Similarly, R is the midpoint of BC 

∴ PR = 1/2 BD           
PR = 1/2 AC  [Diagonal of rectangle are equal ∴ BD = AC]

17. ABCD is a parallelogram, E and F are the mid - points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH. 

Solution

18. BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If L is the mid - point of BC, prove that LM = LN. 

Solution

To prove LM = LN

Draw LS perpendicular to line MN 

∴ The lines BM, LS and CN being the same perpendiculars, on line MN are parallel to each other. 

According to intercept theorem, 

If there are three or more parallel lines and the intercepts made by them on a transversal or equal. Then the corresponding intercepts on any other transversal are also equal. 
In the drawn figure, MB and LS and NC are three parallel lines and the two transversal line are MN and BC 

We have, BL = LC (As L is the given midpoint of BC)
∴ using intercept theorem, we get 

MS = SN ...(i) 
Now in ΔMLS and LSN 

MS = SN  [using ...(i)]

∠LSM  = ∠LSN  = 90°  (LS ⊥ MN and SL = LS common)

∴ ΔMLS ≅ ΔLSN  (SAS congruency theorem)
∴ LM = LN  (CPCT) 

19. Show that the line segment joining the mid - points of the opposite sides of a quadrilateral bisect each other. 

Solution

Let ABCD is a quadrilateral in  which P, Q, R and S are midpoints of sides 

AB, BC, CD and DA respectively join PQ, QR, RS, SP and BD 

In ΔABD, S and P are the midpoints of AD and AB respectively. 
So, by using midpoint theorem we can say that 

SP || BD and SP = 1/2 BD  ...(1) 
Similarly in ΔBCD 
QR || BD and QR = 1/2BD  ...(2) 
From equation (1) and (2) we have 

SP || QR and SP = QR 
As in quadrilateral SPQR one pair of opposite side are equal and parallel to each other. 

So, SPQR is parallelogram 

Since, diagonals of a parallelogram bisect each other. 

Hence PR and QS bisect each other. 

20. Fill in the blanks to make the following statements correct:

(i) The triangle formed by joining the mid-points of the sides of an isosceles triangle is ____

(ii) The triangle formed by joining the mid-points of the sides of a right triangle is ______

(iii) The figure formed by joining the mid-points of consecutive sides of a quadrilateral is _____

Solution

(i) Isosceles

(ii) Right triangle

(iii) Parallelogram