RD Sharma Solutions for Class 9 Chapter 13 Linear Equations in Two Variables Exercise 13.3

Chapter 13 Linear Equations in Two Variables RD Sharma Solutions Exercise 13.3 Class 9 Maths

Chapter Name	RD Sharma Chapter 13 Linear Equations in Two Variables Exercise 13.3
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 13.1 Exercise 13.2 Exercise 13.4
Related Study	NCERT Solutions for Class 10 Maths

Exercise 13.3 Solutions

1. Draw the graph of each of the following linear equation in two variables. 
(i) x + y = 4 
(ii) x - y = 2 
(iii) -x + y = 6 
(iv) y = 2x 
(v) 3x + 5y = 15 
(vi) x/2 - y/3 = 3 
(vii) (x - 2)/3 = y - 3 
(viii) 2y = -x + 1 

Solution

(i) We have x + y = 4 
x = 4 - y
Putting y = 0, we get x = 4 - 0 = 4 
Putting y = 3, we get x = 4 - 3 = 1 
Thus, we get the following table giving the two points on the line represented by the equation x + y = 4 
Graph for the equation  x + y = 4 

(ii) We have,
x - y = 2 
x = 2 +y  ...(i) 
Putting y = 0, we get x = 2 + 0 = 2 
Putting y = -2, we get x = 2 - 2 = 0 
Thus, we get the following table giving the two points on the line represented by the equation x - y = 2 
Graph for the equation x - y = 2 

(iii) We have 
-x + y = 6 
⇒ x = 6 +x 
Putting y = -4, we get y = 6 - 4 = 2
Putting x = -3 we get y = 6 - 3 = 3 
Thus, we get the following table giving the two points on the line represented by the equation -x + y = 6 
Graph for the equation -x + y = 6. 

(iv) We have 
y = 2x  ...(i)
Putting x = 0, we get y = 2 × 0 = 0 
Putting x = 1 we get y = 2×1 = 2
Thus, we get the following table giving the two points on the line represented by the equation y =2x 
Graph for the equation y = 2x

(v) We have 
3x + 5y = 15 
3x = 15 - 5y 
x = (15- 5y)/3 
Putting y = 0, we get x = (15 - 5×0)/3 = 5 
Putting y = 3 we get x = 15 - 5× 3)/3 = 0 
Thus, we get the following table giving the two points on the line represented by the equation 3x + 5y - 15 
Graph for the equation 3x + 5y - 15 

(vi) We have

Putting y = -3, we get x = [12 + 2(-3)]/3 = 2 
Putting y = 0 we get x = (12 + 0)/3 = 4 
Thus, we get the following table giving the two points on the line represented by the equation x/2 - y/3 = 2 
Graph for the equation x/2 - y/3 = 3 

(vii) We have, 

Thus, we get the following table giving the two points on the line represented by the equation (x - 2)/y = y - 3
Graph for the equation (x - 2)/y = y - 3 

(viii) We have 
2y = -x + 1
⇒ x - 1 = 2y ...(1)
Putting y = 0, we get x = 1 - 2×0 = 1 
Putting y = -1, we get x = 1 - 2(-1) = 3 
Thus, we have the following table giving the two points on the line represented by the equation 
2y = x + 3
2y = -x + 1 
Graph for the equation 2y = -x + 1 

2. Given the equations of two lines passing through (3, 12). How many more such lines are there, and why ? 

Solution

The equation of two lines passing through (3, 12)  are 
4x - y = 0 
3x - y + 3 = 0 ...(i) 
There are infinitely many lines passing through (3, 12)

3. A three - wheeler scooter charges Rs 15 for first kilometer and Rs 8 each for every subsequent kilometer. For a distance of x km, an amount of Rs y is paid. Write the linear equation representing the above information. 

Solution

Total fare of Rs. y for covering distance of x kilometers is given by 
y = 15 + 8(x- 1)
⇒ y = 15 + 8x - 8 
⇒ y = 8x + 7 
This is the required linear equation for the given information.

4. A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Aarushi paid Rs 27 for a book kept for seven days. If fixed charges are Rs x and per day charges are Rs y. Write the linear equation representing the above information. 

Solution

Total charges paid by Aarushi is given by 
27 = x + 4y 
⇒ x + 4y = 27 
This is the required linear equation for the given information.

5. A number is 27 more than the number obtained by reversing its digits. If its unit's and ten's digit are x and y respectively, write the linear equation representing the above statement. 

Solution

Total original number is 10y + x 
The new number is obtained after reversing the order of digits is 10x + y
According to question 
⇒ 10y + x = 10x + y + 27 
⇒ 9y - 9x = 27 
⇒ y -x = 3 
⇒ x - y + 3 = 0 
This is the required linear equation for the given information.

6. The sum of a two digit number and the number obtained by reversing the order of its digits is 121. If units and ten's digit of the number are x and y respectively then write the linear equation representing the above statement. 

Solution

Total original number is  10y + x 
The new number is obtained after reversing the order of digits is (10x  y)
According to problem 
(10y +x) + (10x +y) = 121 
⇒ 11x + 11y = 121 
⇒ 11(x + y) = 121 
⇒ x + y = 11 
Thus is the required linear equation for the given information.

7. Plot the points (3, 5) and (-1, 3) on a graph paper and verify that the straight line passing through these points also passes through the point (1, 4). 

Solution

The points given in the graph : 

It is clear from the graph the straight lines passes through these points also pass a through (1, 4).

8. From the choices given below, choose the equation whose graph is given in Fig. below. 
(i) y = x 
(ii) x + y = 0 
(iii) y = 2x 
(iv) 2 + 3y = 7x 

[Hint : Clearly, (-1, 1) and (1, - 1) satisfy the equation x + y = 0 ]

Solution

Clearly (-1, 1) and (1, -1) satisfy the equation x + y = 0 
∴ The equation whose graph is given by x + y = 0

9. From the choices given below, choose the equation whose graph is given in fig. below. 
(i) y = x + 2 
(ii) y = x - 2 
(iii) y = -x + 2 
(iv) x + 2y = 6

[Hint : Clearly, (2, 0) and (-1, 3) satisfy the equation y = -x +2 ]

Solution

Clearly (2, 0) and (-1, 3) satisfy the equation y = -x + 2
∴ The equation whose graph is given by y = -x + 2

10. If the point (2, -2) lies on the graph of the linear equation 5x + ky = 4 , find the value of k. 

Solution

It is given that (2, -2) is a solution of the equation 5x + ky = 4 
∴ 5 × 2 + k ×(-2) = 4 
⇒ 10 - 2k = 4 
⇒ -2k = 4 - 10
⇒ -2k  -6 
⇒ k = 3

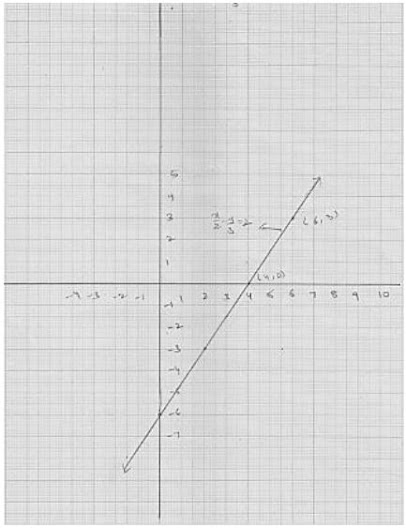
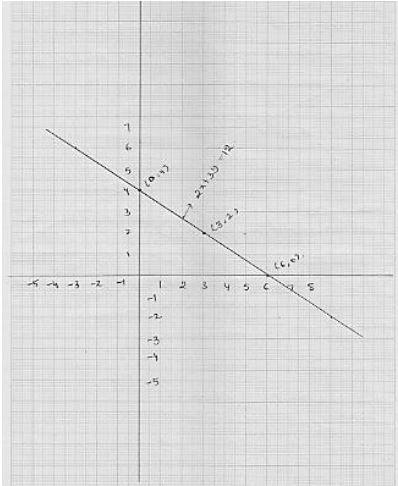
11. Draw the graph of the equation 2x + 3y = 12. From the graph, find the coordinates of the point:

(i) whose y-coordinates is 3.

(ii) whose x - coordinate is -3.

Solution

Graph of the equation 2x + 3y = 12. 
We have, 
2x + 3y = 12 
⇒ 2x = 12 - 3y
⇒ x = (12 - 3y)/2 
Putting y = 2, we get x = (12 -3×2)/2 = 3 
Putting y = -4, we get x = (12 - 3×4)/2 = 0 
Thus, (3, 0) and (0, 4) are two points on the line 2x + 3y = 12
The graph of line represents by the equation 2x + 3y = 12 

X	0	3
Y	4	2

Graph of the equation 2x + 3y = 12 

(i) To find coordinates of the points when y = 3, we draw a line parallel to x - axis and passing through (0, 3) this lines meets the graph of 2x + 3y = 12 at a point p from which we draw a line parallel to y - axis which process x - axis at x = 3/2, so the coordinates of the required points are (3/2, 3).

(ii) To find the coordinates of the points when x = -3 we draw a line parallel to y - axis and passing through (-3, 0). This lines meets the graph of 2x + 3y = 12 at a point P from which we draw a line parallel to x - axis crosses y -axis at y = 6, so, the coordinates of the required point are (-3, 6). 

12. Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes: 

(i) 6x - 3y = 12 
(ii) -x + 4y = 8 
(iii) 2x + y = 6 
(iv) 3x + 2y + 6 = 0

Solution

(i) We have 

6x - 3y = 12 
⇒ 3(2x - y) = 12 
⇒ 2x - y = 4 
⇒ 2x - 4 = y 
⇒ y = 2x - 4 ...(i) 
Putting x = 0 in (i), we get y = -4
Putting x = 2 in (i), we get y = 0 
Thus, we obtain the following table giving coordinates of two points on the line represented by the equation 6x - 3y = 12.
The graph of the line 6x - 3y = 12 

(ii) We have 

-x + 4y = 8 
⇒ 4y - 8 = x
⇒x = 4y = 8 
Putting y = 1 in (i), we get x = 4 × 1 - 8 = -4
Putting y = 2 in (i), we get x = 4 ×2 - 8 = 0 
Thus, we obtain the following table giving coordinates of two points on the line represented by the equation -x + 4y = -8
Graph of the equation -x + 4y = 8

(iii) We have 
2x + y = 6
⇒ y = 6- 2x  ...(i) 
Putting x = 3 in (i), we get y = 6 = 2 × 3 = 0
Putting x = 4 in (i), we get y = 6 - 2× 4 = -2
Thus, we obtain the following table giving coordinate of two points on the line represented by the equation 2x + y = 6 
Graph of the equation 2x + y = 6 

(iv) We have 

3x + 2y + 6 = 0 
⇒ 2y = -6 - 3x 
⇒ y = (-6 - 3x)/2 
Putting x = -2 in (i), we get x = [6 - 3(-2)]/2 = 0 
Putting x = -4 in (i), we get y = [6 - 3(-4)]/2 = 3 
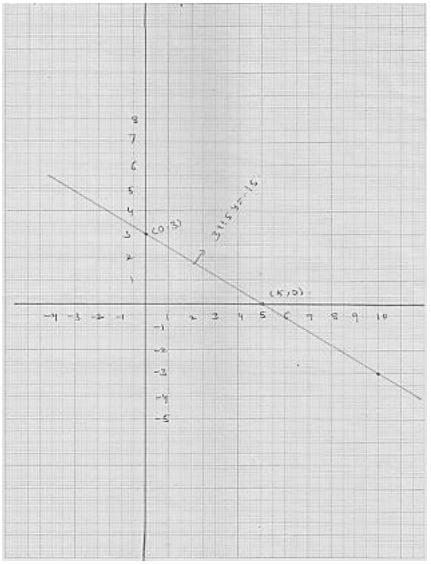
Thus, we obtain the following table giving coordinates of two points on the line represented by the equation 3x + 2y + 6 = 0 
Graph of the equation 3x - 2y + 6 = 0 

13. Draw the graph of the equation 2x + y = 6. Shade the region bounded by the graph and the coordinate axes. Also, find the area of the shaded region. 

Solution

We have 

2x + y = 6 
y = 6 - 2x ...(i) 
Putting x = 3 in (i), we get y = 6 - 2 × 3 = 0 
Putting x = 0 in (i), we get y = 6 - 2 × 0 = 6 
Thus, we obtained the following table giving coordinates of two points on the line represented by the equation 2x + y = 6 

X	3	0
Y	0	6

The graph of line 2x + y  = 6 

14. Draw the graph of the equation x/3 + y/4 = 1. Also, find the area of the triangle formed by the line and the co - ordinates axes.

Solution

We have 

x/3 + y/4 = 1 
⇒ 4x + 3y = 12 
⇒ 4x  = 12 -3y
⇒ x = (12 - 3y)/4 
Putting y = 0 in (i), we get x = (12 - 3×0)/4  = 3 

Putting y = -4  in (ii), we get x = (12 - 3 × 4)/4 = 0 
Thus, we obtained the following table giving coordinate of two points on the line represents by the equation x/3 + y/4 = 1. 

X	0	3
Y	4	0

The graph of line x/3 + y/4 = 1. 

15. Draw the graph of y = |x|. 

Solution

We have 

y = |x|  ...(i) 
Putting x = 0, we get y = 0 
Putting x = 2, we get  y = 2 
Putting x = 2, we get y = -12

Thus, we have the following table for the two points on graph of |x|

X	0	2	-2
Y	0	2	2

Graph of line equation y = | x |

16. Draw the graph of y = |x| + 2

Solution

We have 

y = | x | + 2 ...(i) 
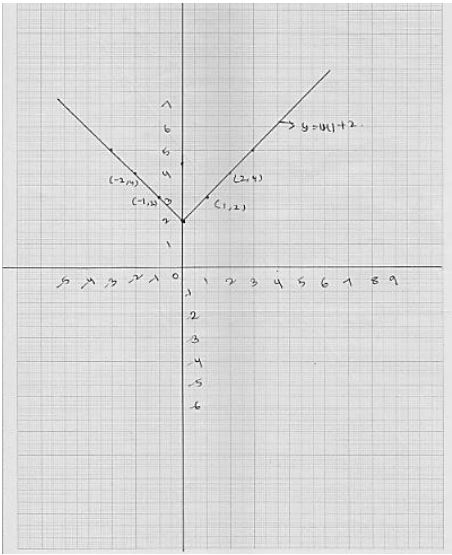
Putting x = 0, we get y = 2 ...(ii)
Putting x = 1, we get y = 3 
Putting x = -1, we get y = 3 

Thus, the we have the following table for the points on graph of | x | + 2

X	0	1	1
Y	2	3	3

Graph of line equation y = | x | + 2 

17. Draw the graphs of the following linear equations on the same graph paper : 2x + 3y = 12, x - y = 1. 
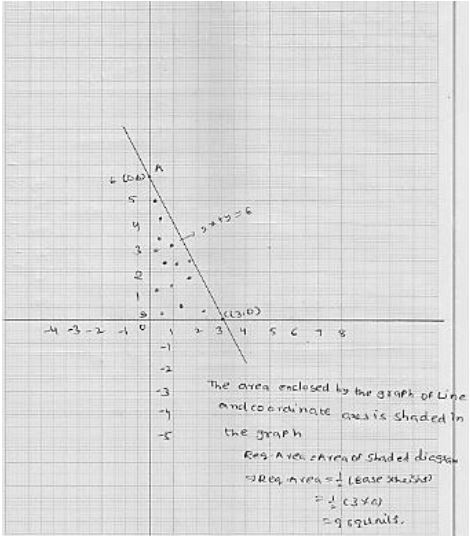
Find the coordinates of the vertices of the triangle formed by the two straight lines and the y - axis. Also, find the area of the triangle. 

Solution

Graph of the equation 2x + 3y - 12 = 0
We have 

2x + 3y = 12 

⇒ 2x = 12 - 3y
⇒ x = (12 - 3y)/2 
Putting y = 4, we get x = (12 - 3× 4)/2 = 0 
Putting y = 2, we get x = (12 - 3×2)/2 = 3 
Thus, we have the following table for the P table for the points on the line 2x + 3y = 12 

X	0	3
Y	4	2

Plotting points A (0, 4), B(3, 2) on the graph paper and drawing a line passing through them 
we obtain graph of the equation. 

Graph of the equation

Graph of the equation x - y -1 : 

We have x - y = 1 ⇒ x = 1 + y
Thus, we have the following table for the points the line x - y = 1

X	1	0
Y	0	-1

Plotting points C(1, 0) and D(0, -1) on the same graph paper drawing a line passing through the m, we obtain the graph of the line represents by the equation x - y = 1.  

Clearly two lines intersect at A (3, 2).
The graph of time 2x + 3y = 12 intersect with y - axis at B(0, 4) and the graph of the line x - y = 1 intersect with y - axis at C(0, -1). 
So, the vertices of the triangle formed by thee two straight lines and y - axis are A(3, 2) and B(0, 4) and C(0, -1)
Now, 

18. Draw the graphs of the linear equations 4x - 3y + 4 = 0 and 4x + 3y - 20 = 0. Find the area bounded by these lines and x - axis.

Solution

We have 

4x - 3y + 4 = 0 
⇒ 4x - 3y = 4

⇒ x = (3y - 4)/4 
Putting y = 0, we get x = (3 × 0 - 4)/4 = - 1 
Putting y = 4, we get x = (3 × 4 - 4)/ 4 = 2 
Thus, we have the following table for the p table for the points on the line 4x - 3y + 4 = 0 

X	-1	2
Y	0	4

We have 

4x + 3y - 20 = 0 
⇒ 4x = 20 - 3y

⇒ x = (20 - 3y)/4 

Putting y = 0, we get x = (20 - 3 ×0)/4 = 5 
Putting y =  4, we get x = (20 - 3 × 4)/4 = 2. 
Thus, we have the following table for the p table for the points on the line 4x - 3y - 20 = 0 

X	0	2
Y	0	4

Clearly, two lines intersect at A(2, 4)
The graph of the lines 4x - 3y + 4 = 0 and 4x + 3y - 20 = 0 intersect with y - axis at a + b(-1, 0) and c(5, 0) respectively 

19. The path of a train A is given by the equation 3x + 4y - 12 = 0 and the path of another train B is given by the equation 6x + 8y - 48 = 0 . Represent this situation graphically.

Solution 

We have, 

3x + 4y - 12 = 0 
⇒ 3x = 12 - 4y 
⇒ 3x = (12 - 4y)/3 

20. Ravish tells his daughter Aarushi, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be". If present ages of Aarushi and Ravish are x and y years respectively, represent this situation algebraically as well as graphically. 

Solution

It is given that seven year ago Harish was seven times a sold as his daughter  

∴ 7(x - y) = y - 7 
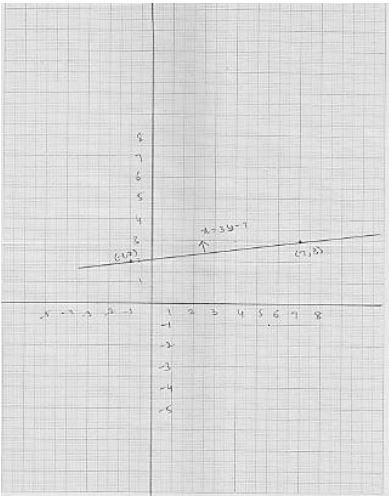
⇒ 7x - 49 = y - 7 
⇒ 7x - 42 = y ...(i)
It is also given that after three years from now Ravish shall be three times a sold as her daughter 

∴ 3(x + 3) = y + 3

⇒ 3x + 9 = y + 3

⇒ 3x + 6 = y  ...(ii)
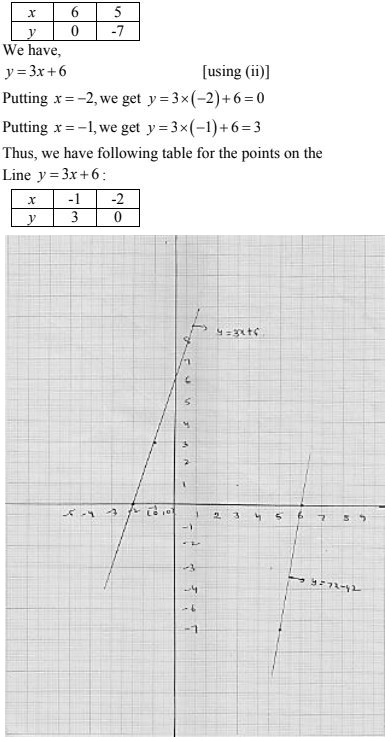
Now, y = 7x - 42  [using (i)]

Putting x = 6, we get y = 7 × 6 - 42 = 0 
Putting x = 5, we get y = 7× 5 - 42 = -7
Thus, we have following table for the points on the 

Line 7x - 42 = y: 

21. Aarushi was driving a car with uniform speed of 60 km/h. Draw distance  - time graph. From the graph, find the distance travelled by Aarushi in 
(i) 2(1/2) Hours 

(ii) 1/2 Hour

Solution

Let x be the time and y be the distance travelled by Aarushi 

It is given that speed of car is 60 km/h
We know that speed= distance/speed 

⇒ 60 = y/x 
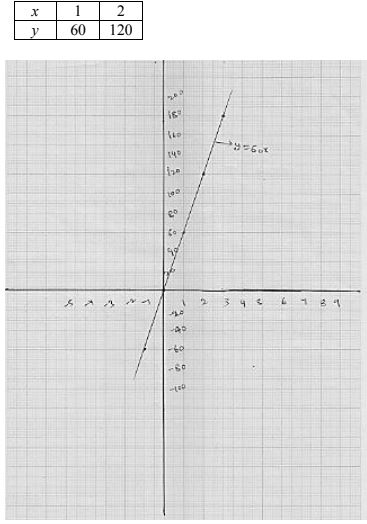
⇒ y = 60x 
Putting x = 1, we get y = 60 
Putting x = 2, we get y = 120 
Thus, we have the following table for the points on the line  y = 60x