RD Sharma Solutions for Class 9 Chapter 12 Heron's Formula Exercise 12.2

Chapter 12 Heron's Formula RD Sharma Solutions Exercise 12.2 Class 9 Maths

Chapter Name	RD Sharma Chapter 12 Heron's Formula Exercise 12.2
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 12.1
Related Study	NCERT Solutions for Class 10 Maths

Exercise 12.2 Solutions

1. Find the area of a quadrilateral ABCD is which AB = 3cm, BC = 4 cm, CD = 4cm, DA = 5 cm and AC = 5 cm. 

Solution

For ΔPQR 

2. The sides of a quadrangular field, taken in order are  26 m, 27 m, 7 m are 24 m respectively.  The angle contained by the last two sides is a right angle. Find its area.

Solution

The sides of a quadrilateral field taken order as AB  = 26m

3. The sides of a quadrilateral, taken in order are 5, 12,14 and 15 meters respectively, and the angle contained by the first two sides is a right angle. Find its area. 

Solution

Given that sides of quadrilateral are AB = 5 m, BC = 12 m, CD = 14 m and DA = 15 m

AB = 5m, BC = 12m, CD = 14 m and DA = 15 m

Join AC

4. A park, in the shape of a quadrilateral ABCD has ∠C = 900, AB = 9m, BC = 12 m, CD = 5 m and AD = 8m . How much area does it occupy ?

Solution

Given sides of a quadrilaterals are AB = 9, BC = 12, CD = 05, DA = 08

Let us joint BD

In ∆BCD applying Pythagoras theorem.

5. Two parallel side of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm.

Find the area of the trapezium.

Solution 

Given that two parallel sides of trapezium are AB = 77 and CD = 60 cm

Other sides are BC = 26 m and AD = 25 cm.

Join AE and CF

Now, DE ⊥ AB and CF ⊥ AB

∴ DC = EF = 60 cm

Let AE = x

⇒ BF = 77 – 60 – x = 17 – x

6. Find the area of a rhombus whose perimeter is 80 m and one of whose diagonal is 24 m.

Solution

Given that,

Perimeter of rhombus = 80m

Perimeter of rhombus = 4 × side

7. A rhombus sheet, whose perimeter is 32 m and whose one diagonal is 10 m long, is painted

on both sides at the rate of Rs 5 per m2. Find the cost of painting.

Solution

Given that,

Perimeter of a rhombus = 32 m

We know that,

Perimeter of rhombus = 4 × side

⇒ 49 = 32m

⇒ a = 8 m

8. Find the area of a quadrilateral ABCD in which AD = 24 ∠BAD = 90° and BCD forms

an equilateral triangle whose each side is equal to 26 cm. (Take √3 = 1.73)

Solution

Given that, a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90°

BCD is equilateral triangle and sides BC = CD = BD = 26 cm

In ∆BAD By using Pythagoras theorem

9. Find the area of a quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm,

DA =34 cm and diagonal BD =20 cm.

Solution

Given that

Sides of a quadrilateral are AB = 42 cm, BC = 21 cm, CD = 29 cm

DA = 34 cm and diagonal BD = 20 cm

Area of quadrilateral = area of ∆ADB + area of ∆BCD.

Now, area of ∆ABD

Perimeter of ∆ABD

We know that

10. Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD =9 cm,

CD = l2cm, ∠ACB = 90° and AC=l5cm.

Solution

The sides of a quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB

= 90° and AC = 15 cm

Here, By using Pythagoras theorem

11. The adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the diagonal

AC measures 42 cm. Find the area of the parallelogram.

Solution

Given that adjacent sides of a parallelogram ABCD measure 34 cm and 20 cm, and the

diagonal AC measures 42 cm.

Area of parallelogram = Area of ∆ADC + area of ∆ABC

[∵ Diagonal of a parallelogram divides into two congruent triangles]

= 2 × [Area of ∆ABC]

Now for Area of ∆ABC

Let 2s = AB + BC + CA [∵ Perimeter of ∆ABC]

12. Find the area of the blades of the magnetic compass shown in Fig.. 12.27.(Take √11 = 3.32).

Solution 

Area of the blades of magnetic compass = Area of ∆ADB + Area of ∆CDB

Now, for area of ∆ADB

Let, 2s = AD + DB + BA (Perimeter of ∆ADB)

13. A hand fan is made by stitching lo equal size triangular strips of two different types of

paper as shown in Fig. 12.28. The dimensions of equal strips are 25 cm, 25 cm and 14 cm.

Find the area of each type of paper needed to make the hand fan.

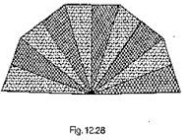
Solution 

Given that the sides of ∆AOB are

AO = 24 cm

OB = 25 cm

BA = 14 cm

Area of each equal strips = Area of ∆le AOB

Now, for area of ∆AOB

Perimeter of ∆AOB

Let 2s = AO + OB + BA

14. A triangle and a parallelogram have the same base and the same area. If the sides of the

triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find

the height of the parallelogram.

Solution 

The sides of a triangle DCE are

DC = 15 cm, CE = 13 cm, ED = 14 cm

Let h be the height of parallelogram ABCD

Given,

Perimeter of ∆DCE

2s = DC + CE + ED