RS Aggarwal Class 10 Solutions Chapter 19 Volume and Surface Area of Solids Exercise 19D

Chapter 19 Volume and Surface Area of Solids RS Aggarwal Solutions Exercise 19D Class 10 Maths

Chapter Name	RS Aggarwal Chapter 19 Volume and Surface Area of Solids
Book Name	RS Aggarwal Mathematics for Class 10
Other Exercises	Exercise 19A Exercise 19B Exercise 19C MCQ
Related Study	NCERT Solutions for Class 10 Maths

Volume and Surface Area of Solids Exercise 19D Solutions

1. A river 1.5 m deep and 36 m wide is flowing at the rate of 3.5 km/hr. Find the amount of water (in cubic metres) that runs into the sea per minute.

Solution

Given,

Depth of the river = 1.5 m

Width of the river = 36 m

Flow rate of river = 3.5 km/hr

Now first change the rate of flow of the water in meter/min

As we know,

1km = 1000 m

⇒ 1 hour = 60 minutes

So,

3.5 km/r = 3.5 km/1 hour

= (3.5 × 1000 m)/(1 × 60 min)

= 350/6 m/min

River travel in a minute = 350/6 m

Now,

The amount of water that runs into sea per minute;

350/6 × 1.5 × 36 = 350 × 1.5 × 6 = 3150

So,

The amount of water that runs into the sea per minute is 3150 m³

2. The volume of a cube is 729 cm³. Find its surface area.

Solution

Given,

Volume of the cube = 729 cm³

Let the edge of the cube = a cm

So,

Volume (v) of the cube = a³

a³ = 729

⇒ a³ = (9 cm)³

⇒ a = 9 cm

Lateral surface area of cube = 4a²

= 4 × 92

= 4 × 81

= 324 cm²

Total surface area of the cube = 6a2

= 6 × 9²

= 6 × 81

= 486 cm²

3. How many cubes of 10 cm edge can be put in a cubical box of 1 m edge ?

Solution

Given,

Edge of the Cubical Box = 1 m

Volume of the Cubical Box = a³

Edge of the cubes = 10 cm

Volume of the cube = a³

Number of cubes = Volume of box/Volume of the cube

= 100 × 100 × 100/10 × 10 × 10

= 1000000/1000

= 1000 cubes

4. Three cubes of iron whose edges are 6 cm, 8 cm and 10 cm respectively are melted and formed into a single cube. Find the edge of the new cube formed.

Solution

Given,

Edge of the first cube = 6 cm

Volume of the first cube = a³ = (6)³ cm

Edge of the second cube = 8 cm

Volume of the second cube = a³ = (8)³ cm

Edge of the third cube = 10 cm

Volume of the third cube = a³ = (10)³ cm

So,

Volume of the formed cube = Volume of the first + Second + Third Cube

Volume of the formed cube = v1 + v2 + v3 

= 6³ + 8³ + 10³

= 216 + 512 + 1000

= 1728

Now volume of new cube = a³ = 1728

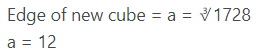
Therefore surface area of new cube = 6a²

= 6 × 12²

= 6 × 12 × 12

= 864 cm²

5. Five identical cubes, each of edge 5 cm, are placed adjacent to each other. Find the volume of the resulting cuboid.

Solution

Given,

Edge of the given cube = 5 cm

Now,

Length (l) of the resulting cuboid = Edge × Number of cubes

= 5 × 5

= 25 cm

Breadth (b) of the resulting cuboid = 5 cm

Height (h) of the resulting cuboid = 5 cm

So,

Volume of the resulting cuboid = l×b×h

= 25 × 5 × 5

= 625 cm³

Hence,

The volume of the resulting cube is 625 cm³

6. The volumes of two cubes are in the ratio 8: 27. Find the ratio of their surface areas.

Solution

Given,

Ratio of two cube = 8 : 27

Let the edges of the cubes to c and y

As,

⇒ (Volume of the first cube)/(Volume of the second cube) = 8/27

⇒ x³/y³ = 8/27

x/y = 2/3 …(i)

Now,

The ratio of the surface areas of the cubes = (Surface area of the first cube)/(Surface area of the second cube)

⇒ 6x²/6y² = (x/y)²

= (2/3)² …[Using (i)]

= 4/9

= 4 : 9

So,

The ratio of the surface areas of the given cubes is 4 : 9.

7. The volume of a right circular cylinder with its height equal to the radius is 25.1/7 cm³. Find the height of the cylinder.

Solution

Given,

Radius of the right circular cylinder = 176/7 cm³

Height of the right circular cylinder = radius of the right circular cylinder

So,

⇒ h = r

As,

Volume of the right circular cylinder = 176/7 cm³

⇒ πr²h = 176/7

⇒ 22/7 × h² × h = 167

⇒ h³ = 176 × 7/7 × 22

⇒ h³ = 8

⇒ h = 3√8

Therefore,

h = 2 cm

So,

The height of the right circular cylinder is 2 cm

8. The ratio between the radius of the base and the height of a cylinder is 2 : 3. If the volume of the cylinder is 12936 cm³. Find the radius of the base of the cylinder.

Solution

Given,

Ratio of the base and the height of a cylinder is 2 : 3.

So,

Let the radius of the base = r

And

The height of the cylinder = h

r : h = 2 : 3

That is,

r/h = 2/3

So,

h = 3r/2 …(i)

As,

Volume of the cylinder = 12936 cm³

⇒ 22/7 × r² × 3r/2 = 12936 [Using (i)]

⇒ 33/7 × r³ = 12936

⇒ r³ = 12936 × 7/33

⇒ r³ = 2744

⇒ r = 3√2744

Therefore,

r = 14 cm

So,

The radius of the base of the cylinder is 14 cm.

⇒ πr²h = 12936.

9. The radii of two cylinder are in the ratio 2 : 3 and their height are in the ratio of 5 : 3. Find the ratio of their volumes.

Solution

Let the radius of the first cylinder = r₁

And the radius of the second cylinder = r₂;

Let the height of first cylinder = h₁

And the height of second cylinder = h₂

Given,

r₁ : r₂ = 2 : 3

⇒ r₁/r₂ = 23 …(i)

And

h₁ : h₂ = 5 : 3

⇒ h₁/h₂ = 5/3 …(ii)

Now,

The ratio of the volumes of the cylinders = (Volume of first cylinder)/(Volume of second cylinder)

So,

The ratio of the volumes of the given cylinders is 20: 27.

10. 66 cubic cm of silver is drawn into a wire 1 mm in diameter. Calculate the length of the wire in metres.

Solution

Given,

Volume of the wire = 66 cm³

Diameter of the wire = 1 mm

Radius (r) of wire = 12 = 0.5 mm = 0.05 cm

Let the length of the wire be l

As,

Volume of the wire = 66 cm³

⇒ πr²l = 66

⇒ 22/7 × 0.05 × 0.05 × l = 66

⇒ l = 66 × 722 × 0.05 × 0.05

Therefore,

l = 8400 cm = 84 m

So,

The length of the wire is 84 m.

11. If the area of the base of a right circular cone is 3850 cm² and its height is 84 cm, find the slant height of the cone.

Solution

Given,

Area of the base of the right circular cone = 3850 cm²

Height of the right circular cone = 84 cm

Let the radius of the cone = r

And the slant height of the cone = l

As,

Area of the base of the cone = 3850 cm²

⇒ πr² = 3850

⇒ 22/7 × r² = 3850

⇒ r² = 3850 × 7/22

⇒ r² = 1225

⇒ r = √1225

Therefore,

r = 35 cm

Now,

Length = √h² + r²

= √(84)² + (35)²

= √7056 + 1225

= √8281

= 91 cm

So,

The slant height of the given cone is 91 cm.

12. A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. Calculate the radius of the base of the cone.

Solution

Given,

Base radius (r) of the cylinder = 8 cm

Height (h) of the cylinder = 2 cm and

Height (H) of the cone = 6 cm

Let the base radius of the cone = R

Now,

As the cylinder is melted to form the cone,

So,

Volume of the cone = volume of the cylinder

⇒ 1/3πR²H = πr²h

⇒ R² = 3r²hH

⇒ R² = 3 × 8 × 8 × 26

⇒ R² = 64

⇒ R = √64

Therefore,

R = 8 cm

So,

The radius of the base of the cone is 8 cm.

13. A right cylindrical vessel is full of water. How many right cones having the same radius and height as those of the right cylinder will be needed to store that water?

Solution

Let suppose the radius of the cone = r

And height of the cone = h,

Then,

Radius of the cylindrical vessel = r and

Height of the cylindrical vessel = h

Now,

The required number of cones = (Volume of the cylindrical vessel)/(Volume of a cone)

= (πr²h)/(1/3πr²h)

= 3

So,

The number of the cones that is required to store the water is 3.

14. The volume of a sphere is 4851 cm³. Find its curved surface area.

Solution

The volume of the sphere = 4851 cm³

Let the radius of the sphere = r

As,

Volume of the sphere = 4851 cm³

⇒ 4/3 πr³ = 4851

⇒ 4/3 × 2/7 × r³ = 4851

⇒ r³ = 4851 × (3 × 7)/(4 × 22)

⇒ r³ = 92618

⇒ r = 3√92618

⇒ r = 212 cm

Now,

The curved surface area of the sphere = 4πr²

= 4 × 22/7 × 21/2 × 21/2

= 1386 cm²

So,

The curved surface area of the sphere is 1386 cm²

15. The curved surface area of a sphere is 5544 cm³. Find its volume.

Solution

Given,

Curved surface area of the sphere = 5544 cm³

Let the radius of the sphere = r

As we know,

Curved surface area of the sphere = 4πr²

So,

⇒ 4πr² = 5544

⇒ 4 × 22/7 × r² = 5544

⇒ r² = 5544 × 7/(4 × 22)

⇒ r² = 441

⇒ r = √441

⇒ r = 21 cm

Now,

Volume of the sphere = 4/3πr³

= 4/3 × 22/7 × 21 × 21 × 21

= 38808 cm³

So,

The volume of the sphere is 38808 cm³.

16. The surface areas of two sphere are in the ratio of 4 : 25. Find the ratio of their volumes.

Solution

Let suppose the radius of first spheres = r

And the radius of second spheres = R

As per the question,

Surface area of the first sphere/Surface area of the second sphere = 4/25

⇒ 4πr²/4πR² = 4/25

⇒ (r/R)²  = 4/25

⇒ r/R = √4/25

⇒ r/R = 2/5 …(ii)

Now,

The ratio of the volumes of the two sphere = (Volume of the first sphere)/(Volume of the secons sphere)

= (4/3πr³)/(4/3πR³)

= (r/R)³

= (2/5)³ …[Using (i)]

= 8/125

= 8 : 125

So,

The ratio of the volumes of the given spheres will be 8 : 125.

17. A solid metallic sphere of radius 8 cm is melted and into spherical balls each of radius 2 cm. Find the number of spherical balls obtained.

Solution

Given,

Radius (R) of the solid metallic sphere = 8 cm

Radius (r) of the spherical ball = 2 cm

Now,

The number of spherical balls obtained = (Volume of the solid metallic sphere)/(Volume of the spherical ball)

= (4/3πr³)/(4/3πR³)

= (R/r)³

= (8/2)³

= 4³

= 64

So, the number of spherical balls obtained is 64.

18. How many lead shots each 3 mm in diameter can be made from a cuboid of dimensions 9 cm × 12 cm?

Solution

Given,

Diameter of the lead shot = 3 mm

Radius (r) of a lead shot = 3/2 = 1.5 mm = 0.15 cm and

Dimensions of the cuboid = 9 cm × 11 cm × 12 cm

Now,

The number of the lead shots = (Volume of the cuboid)/(Volume of a shot)

= (9 × 12 × 12)/(4/3πr³)

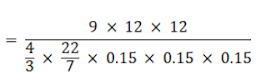
= 84000

So,

84000 number of lead shots can be made from the cuboid.

19. A metallic cone of radius 12 cm height 24 cm is melted and made onto spheres of radius 2 cm each. How many spheres are formed ?

Solution

Cone:

Radius = 12 cm

Height = 24 cm

Sphere, radius = 2 cm

Volume of cone is given as, V = 1/3 × π × r² × h

⇒ V = 1/3 × 22/7 × 12² × 24

⇒ V = 3620 cm³

Volume of sphere, V = 4/3 × π × r³

⇒ V = 4/3 × π × 2³

⇒ V = 33.52 cm³

∴ The number of squares formed will be 3620/34 = 106

20. A hemisphere of lead of radius 6 cm is cast into a right circular cone of height 75 cm. Find the radius of the base of the cone.

Solution

Given,

Radius (R) of the hemisphere = 6 cm

Height (h) of the cone = 75 cm

Let the radius of the base of the cone = r

Now,

Volume of the cone = Volume of the hemisphere

⇒ 1/3πr²h = 2/3πr³

⇒ r² = 2R³/h

⇒ r² = (2 × 6 × 6 × 6)/75

⇒ r² = 5.76

⇒ r = √5.76

Therefore,

r = 2.4 cm

So,

The radius of the base of the cone is 2.4 cm.

21. A copper sphere of diameter 18 cm is drawn into wire of diameter 4 mm. Find the length of the wire.

Solution

The basic concept required to solve any such question is that the volume of the two figures will be same, so here we will equate the volume of sphere to that of wire which is in shape of a cylinder and subsequently will find out the height of the cylinder.

Given diameter of copper sphere = D = 18 cm

∴ Radius of the sphere = R = d/2 = 18/2 = 9 cm

As we know the wire is cylindrical in shape so,

Let the height of the cylindrical wire be ‘h’ cm

Given diameter of cylindrical wire = d = 4 mm

⇒ Radius of the cylindrical wire = r = d/2 = 4/2 = 2 mm = 0.2 cm

(∵ 1 mm = 0.1 cm)

Volume of a sphere = 4/3πR³ (where R = radius of sphere) ...(i)

= 4/3π(9³) (putting value of R in eqn 1)

= 4/3 × π × 729

⇒ Volume of sphere = 4π × 243 = 972π cm³ ...(ii)

Volume of cylinder = πr²h

Where r = radius of base of cylinder and h = height of cylinder

⇒ Volume of cylindrical wire = π × (0.2)² × h (putting value of r)

= 0.04π × h cm³ ...(iii)

Now on equating equation 2 and equation 3, we get,

Volume of sphere = Volume of cylindrical wire

⇒ 972π = 0.04 πh

⇒ π(927) = π(0.04h) (taking π common on both sides)

⇒ 927 = 0.04h

⇒ 972/(0.04) = h

∴ h = 24300 cm

The height of cylindrical wire is 24300 cm or 243 m.

22. The radii of the circular ends of a frustum of height 6 cm are 14 cm and 6 cm respectively. Find the slant height of the frustum.

Solution

Given height of frustum = h = 6 cm

Radius of top = r = 6 cm

Radius of bottom = R = 14 cm

Let the slant height of the frustum be ‘l’ cm

We know in frustum

(Slant height)² = (height)² + (R – r)² ...(i)

⇒ l² = 6² + (14 – 6)² (putting values of r, r and h in eqn1)

⇒ l² = 36 + 8²

⇒ l² = 36 + 64

⇒ l² = 100

⇒ l = √100

∴ l = 10 cm

Slant height of the frustum is 10 cm.

23. Find the ratio of the volume of a cube to that of a sphere which will fit inside it.

Solution

Let the radius of the sphere be ‘R’ units

And the cube which will fit inside it be edge ‘a’ units

Explanation: The longest diagonal of the cube that will fit inside the sphere will be the diameter of the sphere.

∴ The longest diagonal of cube = the diameter of the sphere

Consider △BCD, ∠BDC = 90°

BD = CD = a units (as they are the edges of cube)

BC² = CD² + BD² (Pythagoras theorem)

⇒ BC² = a² + a² (putting value of BD and CD)

⇒ BC² = 2a²

⇒ BC = √(2a²)

∴ BC = a√2 units ...(i)

Now consider △ABC, ∠ABC = 90°

Here, AB = a units and BC = a√2 units

AC² = AB² + BC² (Pythagoras theorem)

⇒ AC² = a² + (a√2)² (putting values of AB and BC)

⇒ AC² = a² + 2a²

⇒ AC² = 3a²

⇒ AC = (√3a²)

∴ AC = a√3 units

∴ Diameter of sphere = D = a√3 units

And we know, D = 2 × R

⇒ R = D/2 (put value of D)

∴ R = (a√3)/2 units

Also, Volume of a sphere = 4/3πR³ ...(ii)

Put value of R in (ii)

= 4/3π(a√3/2)²

= (4 × π × 3a²)/(3 × 4)

∴ Volume of sphere = πa² cubic units ...(iii)

Volume of cube = (edge)³

∴ Volume of cube = a³ cubic units ...(iv)

Ratio of volume of cube to that of sphere = (Volume of cube)/(Volume of sphere)

= a²/π(a)² (putting values from eqn3 and eqn4)

⇒ Ratio of volume of cube to that of sphere = a²/(π × a²)

= a/π

Ratio of volume of cube to that of sphere is a: π.

24. Find the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?

Solution

Let the radius of cylinder, cone and sphere be ‘r’ cm

Let the diameter of cylinder, sphere and cone be ‘2r’ units

∴ Height of cylinder, cone, sphere = h = 2r units

Volume of cylinder = π(r²)h

⇒ Volume of cylinder = π × r² × 2r (putting value of h)

∴ Volume of cylinder = 2π × r³ ...(i)

Volume of sphere = 4/3.π(r)³

= (4π × r³)/3 ...(ii)

Volume of cone = 1/3π(r)²h (put the value of h)

⇒ Volume of cone = (π × r² ×2r)/3

∴ Volume of cone = (2π × r³)/3 ...(iii)

Ratio of volume of cylinder to that of a cone to that of a sphere as:

⇒ Volume of cylinder : Volume of Cone : Volume of sphere

⇒ 2π × r³ : (2π × r³)/3 : (4π × r³)/3

⇒ 2 : 2/3 : 4/2 (dividing the above relation by (πr³)

⇒ 1 : 1/3 : 2/3 (dividing the above ratio by 2)

⇒ 3 : 1 : 2 (multiplying the above ratio by 3)

Ratio of volume of cylinder to that of cone to that of sphere is 3 : 1 : 2.

25. Two cubes each of volume 124 cm³ are joined end to form a solid. Find the surface area of the resulting cuboid.

Solution

Given volume of each cube = 125 cm³

Let the edge of each cube be ‘a’ cm

So, Volume of cube = a³

⇒ a³ = 125

∴ a = 5 cm ...(i)

Now when we join the two cubes then resulting cuboid will be of length twice that of the cube and breadth and height of the resulting cuboid will be same as that of the cube.

⇒ Length of cuboid = L = 2 × a

⇒ L = 2 × 5 (putting value of a from eqn 1)

∴ L = 10 cm

Now, breadth of cuboid = B = a

⇒ B = 5 cm

Similarly, height of the cuboid = H = 5 cm

Note: Where ever in a question

Surface Area is mentioned, it means

Total surface area.

Surface area = Total surface area = 2(LB +BH + HL)

⇒ S.A = 2(10 × 5) + (5 × 5) + (10 × 5)

⇒ S.A = 2(50 + 25 + 50)

⇒ S.A = 2 × 125

∴ S.A = 250 cm²

Surface Area of resulting cuboid is 250 cm².

26. Three metallic cubes whose edges are 3 cm, 4 cm and 5 cm, area melted and recast into a single large cube. Find the edge of the new cube formed.

Solution

Let the edges of cubes be a₁, a₂ and a₃

So, a₁ = 3 cm, a₂ = 4 cm, and a₃ = 5 cm

Explanation: Here the sum of volumes of all three cubes will be equal to the volume of the resulting larger cube as the resulting cube is formed by melting the three cubes.

Volumes of cube with edge a₁ = v₁ = (a₁)³

⇒ v₁ = (3)³

∴ v₁ = 27 cm³ ...(i)

Similarly,

Volume of cube with edge a₂ = v₂ (a₂)³

⇒ v₂ = (4)³

∴ v₂ = 64 cm³ ...(ii)

Volume of cube with edge a₃ = v₃ = (a₃)³

⇒ v₃ = (5)³

∴ v₃ = 125 cm³ ...(iii)

Now let the volume of resulting cube be ‘V’ cm³

So, V = v₁ + v₂ + v₃

⇒ V = 27 + 64 + 125 (from eqn1, eqn2 and eqn3)

∴ V = 216 cm³ ...(iv)

Let the edge of resulting cube be ‘a’ cm

So, volume of the resulting cube = V = a³ ...(v)

Equate equation 4 and 5,

⇒ a³ = 216

∴ a = 6 cm

The edge of new cube formed is 6 cm.

27. A solid metallic sphere of diameter 8 cm is melted and drawn into a cylindrical wire of uniform width. If the length of the wire is 12 m, find its width.

Solution

Let the diameter of sphere be ‘D’ and Radius of sphere be ‘R’

∴ D = 8 m

Also, we know

R = D/2

⇒ R = 8/2

∴ R = 4 m

Explanation: Here the volume of sphere will be equal to the volume of the resulting cylinder as the resulting cylinder is formed by melting the sphere.

Volume of sphere, V₁ = 4/3πR³ (put the value of R)

= 4/3π(4³)

= (4π × 64)/3

= (256π)/3 m³ ...(i)

Let the length/height of the cylinder be ‘H’ and let the radius of the cylinder be ‘r’ and volume of the cylinder be ‘V₂’.

∴ H = 12 m

Volume of the cylinder = V₂ = π(r²)H

⇒ V₂ = π(r²) × 12 (putting value of H)

⇒ V₂ = 12π × r² m³ ...(ii)

Now equate equation 1 and 2,

⇒ V₂ = V₁

⇒ 12π × r² = (256π)/3

⇒ r² = (256π)/(3 × 12π)

⇒ r² = 256/36

⇒ r² = 64/9

⇒ r = 8/3

∴ r = 2.66 m

Width of cylinder = diameter of cylinder = 2 × radius

⇒ Width of cylinder = 2 × r

⇒ Width of cylinder = 2 × 2.66

∴ Width of cylinder = 5.32 m

Width of the resulting cylinder is 5.32 m

28. A 5 m-wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used, at the rate of Rs 25 per metre.

Solution

Let the length of the cloth used be ’L’ cm

Area of cloth used = 5 × l ...(i)

Also, Given diameter = d = 14 m and height = h = 24 m

∴ Radius = r = D/2

⇒ r = 14/2

∴ r = 7 m

Let the slant height of the cone be l m

So, (Slant height)² = (Height)² + (Radius)²

Put the values in the above relation

⇒ l² = h² + r²

⇒ l² = 24² + 7² 

⇒ l² = 576 + 49

⇒ l² = 625

⇒ l = √(625)

∴ l = 25 cm ...(i)

Also, we know Curved Surface Area of cone = πrl

Where r = radius of base, l = slant height

C.S.A. = π × 7 × 25

⇒ C.S.A = 22/7 × 7 × 25 (π = 22/7)

⇒ C.S.A = 22 × 25

⇒ C.S.A = 550 m² ...(ii)

Now the Curved surface area of conical tent will be equal to the area of the cloth used to make the tent

⇒ C.S.A = Area of cloth

⇒ 550 = 5 × L (from eqn1 and eqn2)

⇒ L = 550/5

∴ L = 110 m

So, cost of the cloth used = rate of cloth × length of the cloth

⇒ Cost of cloth used = 25 × 110

⇒ Cost of cloth = Rs 2750

Cost of the cloth used is Rs 2750.

29. A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, find the volume of wood in the toy.

Solution

Given height of cylinder = h = 10 cm

Radius of cylinder = r = 3.5 cm

Radius of hemisphere = R = 3.5 cm

Explanation : In this question the volume of wood in toy can be calculated by subtracting the volume of two hemisphere from the volume of cylinder.

So, volume of cylinder = πr²h

Where r = radius of cylinder and h = height of cylinder

⇒ Volume of cylinder = π × (3.5)² × 10 (from given values)

⇒ Volume of cylinder = π × 12.25 × 10

∴ Volume of cylinder = 122.5π cm³ ...(i)

Volume of a hemisphere = 2/3 πR³ (where R is radius of hemisphere)

= 2/3 × π × (3.5)³

= (2π × 42.875)/3

= 85.75π/3 cm³

= 2 × (85.75π)/3

∴ Volume of two hemisphere = (171.5π)/3 cm³ ...(ii)

Volume of wood in toy = eqn1 – eqn2

⇒ Volume of wood in toy = 122.5π – (171.5π)/3

= (122.5 – 171.5/3)π (taking π common)

= (367.5 – 171.5)/3 π

= (196/3)π (put π = 22/7)

= (196/3 × 22/7)

= (28 × 22)/3

∴ Volume of wood in toy = 205.333 cm³

Volume of wood in toy is 205.333 cm³.

30. Three cubes of a metal whose edge are in the ratio 3 : 4 : 5 are melted and converted into a single cube whose diagonal is 12√3 cm. Find the edges of the three cubes.

Solution

Let the edges of metal cubes be a₁, a₂ and a₃

And it is given that ratio of edges is 3 : 4 : 5

So, let a₁ = 3x, a₂ = 4x and a₃ = 5x

Volume of cube with edge a₁ = v₁ = (a₁)³

⇒ v₁ = (3x)³

∴ v₁ = 27x³ cm³ ...(i)

Similarly

Volume of cube with edge a₂ = v₂ = (a₂)³

⇒ v₂ = (4x)³

∴ v2 = 64x³ cm³ ...(ii)

Volume of cube with edge a₃ = v₃ = (a₃)³

⇒ v₃ = (5x)³

∴ v₃ = 125x³ cm³ ...(iii)

Now let the volume of resulting cube be ‘V’ cm³

So, V = v₁ + v₂ + v₃

⇒ V = 27x³ + 64x³ + 125x³ (from eqn1, eqn2 and eqn3)

∴ V = 216x³ cm³ ...(iv)

It is given that the diagonal of the resulting cube is 12√3 cm

Let the edge of resulting cube be ‘a’ cm

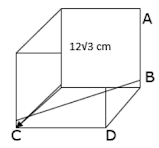
Consider △BCD, ∠BDC = 90°

BD = CD = a cm (as they are the edges of cube)

BC² = CD² + BD² (Pythagoras theorem)

⇒ BC² = a² + a² (putting value of BD and CD)

⇒ BC² = 2a²

⇒ BC = (√2a²)

∴ BC = a√2 cm

Now consider △ABC, ∠ABC = 90°

Here, AB = a cm and BC = a√2 cm and AC = 12√3 cm

AC² = AB² + BC² (Pythagoras theorem)

⇒ (12√3)² = a² + (a√2)² (putting values of AB, AC and BC)

⇒ 144 × 3 = a² + 2a²

⇒ 144 × 3 = 3a²

⇒ 144 = a²

⇒ a = √144

∴ a = 12 cm

So, volume of the resulting cube = V = a³

⇒ V = 12³ (putting value of a)

∴ V = 1728 cm³ ...(v)

Equate equation 4 and 5

⇒ 216x³ = 1728

⇒ x³ = 1728/216

⇒ x³ = 8

∴ x = 2

So, a₁ = 3x = 3 × 2

⇒ a₁ = 6 cm

Similarly, a₂ = 4x = 4 × 2

∴ a₂ = 8 cm

Similarly a₃ = 5x = 5 × 2

∴ a₃ = 10 cm

The edges of three cubes are 6 cm, 8 cm and 10 cm.

31. A hollow sphere of external and internal diameter 8 cm and 4 cm respectively is melted into a solid cone of base diameter 8 cm. Find the height of the cone.

Solution

External diameter of hollow sphere = D = 8 cm

⇒ External radius of hollow sphere = R = D/2

⇒ R = 8/2

⇒ R = 4 cm

Internal diameter of hollow sphere = d = 4 cm

⇒ Internal radius of hollow sphere = r = d/2

⇒ r = 4/2

⇒ r = 2 cm

Let the height of the resulting cone be ‘h’ cm

Let the volume of external sphere be V₁ and that of internal be V₂.

Explanation: Here the volume of hollow sphere will be equal to the volume of the resulting cone as the resulting cine is formed by melting the sphere.

Volume of the External sphere = V₁ = 4/3πR³ (put the value of R)

= 4/3π(4³)

= (4π × 64)/3

= 256π/3 cm³ ...(i)

Volume of the Internal sphere = V₂ = 4/3πr³ (put the value of r)

= 4/3π(2³)

= (4π × 8)/3

∴ Volume of the Internal sphere = V₂ = (32π)/3 cm³ ...(ii)

Volume of sphere = V = External volume – Internal volume

⇒ V = (256π/3 - 32π/3)

⇒ V = (256 – 32)π/3

⇒ V = 224π/3 cm³ ...(iii)

Given base radius of the resulting cone = r’ = 8 cm

Let the height be ‘h’ and volume of the resulting cone be V’

⇒ V’ = 1/3π(r’)²h

⇒ V’ = 1/3π(8²)h (putting value of r’)

⇒ V’ = (64πh)/3 cm³ ...(iv)

Equate equation 3 and 4,

⇒ V = V’

⇒ 224π/3 = 64πh/3

⇒ 224 = 64h

⇒ h = 224/64

 ∴ h = 3.5 cm

The height of resulting cone is 3.5 cm.

32. A bucket of height 24 cm is in the form of frustum of a cone whose circular ends are of diameter 28 cm and 42 cm. Find the cost of milk at the rate of Rs 30 per litre, which the bucket can hold.

Solution

Upper end radius of frustum = d/2 = 28/2 = 14 cm

Lower ends radius of frustum = D/2 = 42/2 = 21 cm

Height of the frustum = 24 cm

And we know,

The amount of milk that bucket can hold = Volume of the bucket

And, Volume of bucket = Volume of Frustum

∴ Amount of milk that bucket can hold = Volume of frustum

⇒ Volume of frustum = 1/3 × π × h × (r² + R² + (r + R))

Where R = Radius of larger or lower end and r = Radius of smaller or upper end and h = height of frustum π = 22/7

⇒ Volume of frustum = 1/3 × 22/7 × (14² + 21² + (14 × 21)

= 22/7 × 8 × (196 + 441 + 294)

= 22/7 × 8 × 931

= 22 × 8 × 133

∴ Volume of frustum = 23408 cm³

Also we know that 1 litre = 1000 cm³

⇒ Volume of frustum in litre = 23408/1000 = 23.408 litre

⇒ Amount of milk that the bucket hold = 23.408 litre

⇒ The cost of milk = rate of milk × amount of milk bucket holds

⇒ The cost of milk = 30 × 23.408

= Rs 702.24

The cost of milk is Rs 702.24

33. The interior of a building is in the form of a right circular of diameter 4.2 m and height 4 m surmounted by a cone of same diameter. The height of the cone is 2.8 m. Find the outer surface area of the building.

Solution

Explanation: Here in order to find the outer surface area of building we need to simply add the curved surface areas of cone and cylinder.

Given height of cylinder = h = 4 m

Height of cone = h’ = 2.8 m

Diameter of cylinder = diameter of cone = d = 4.2 m

⇒ Radius of cone = Radius of cylinder = d/2 = 4.2m/2 = 2.1 m

Outer surface area of building = C.S.A of cylinder + C.S.A of cone

Now, C.S.A of cylinder = 2πrh ...(i)

Where r = radius of base of cylinder, h = height of cylinder

And C.S.A of cone = πrl ...(ii)

Where r = radius of base of cone, l = Slant height of cone

We know in a cone

(Slant height)² = (height)² + (radius)² (put the given values)

(l)² = (2.8)² + (2.1)²

⇒ (l)² = 7.84 + 4.41

⇒ (l)² = 12.25

⇒ l = √(12.25)

∴ l = 3.5 m

Now, C.S.A of cone = π × 2.1 × 3.5 (putting the values in eqn2)

⇒ C.S.A of cone = 7.35π m² ...(iii)

C.S.A of cylinder = 2 × π × 2.1 × 4 (putting the values in eqn1)

⇒ C.S.A of cylinder = 2 × π × 4.41 × 4

∴ C.S.A of cylinder = 16.8π m² ...(iv)

Outer surface area of building = eqn3 + eqn4

⇒ Outer surface area = 7.35π + 16.8π

= 24.15π

∴ Outer surface area = 75.9 m²

The outer surface area of building is 75.9 m².

34. A metallic solid right circular cone of height 84 cm and the radius of its base is 21 cm. It is melted and recast into a solid sphere. Find the diameter of the sphere.

Solution

Let the Radius of cone be ‘r’ and height of cone be ‘h’

∴ r = 21 cm and h = 84 cm

Explanation: Here the volume of cone will be equal to the volume of the resulting sphere as the resulting sphere is formed by melting the cone.

Volume of cone, V₁ = 1/3π(r²)h

⇒ V₁ = 1/3 × π × (21)² × 84

⇒ V₁ = π × 441 × 28

∴ V₁ = 12348π m³ ...(i)

Let the Radius f resulting sphere be r’ cm

Volume of the sphere = V₁ = 4/3(R³) ...(ii) (put the value of R)

Now equate equation 1 and 2,

⇒ V₂ = V₁

⇒ 4/3π(R)³ = 12348π

⇒ (4 × R³)/3 = 12348

⇒ R³ = (12348 × 3)/4

⇒ R³ = 3087 × 3

⇒ R³ = 9261

∴ R = 21 cm

Diameter of Sphere = 2 × radius

⇒ Diameter of Sphere = 2 × R = 42 m

Diameter of the resulting Sphere is 42 m.

35. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.

Solution

Explanation: the total surface area of the toy can be calculated by taking the sum of the Curved surface area of cone and that of hemisphere of same radius.

Given total height of toy = H = 15.5 cm

Radius of hemisphere = Radius of cone = r = 3.5 cm

Now the height of cone = h = total height – radius of hemisphere

⇒ Height of cone = h = 15.5 – 3.5

∴ Height of cone = h = 12 cm

Let the slant height of the cone be ‘l’ cm

Also we know that in a cone,

(Slant height)² = (Height)² + (Radius)²

⇒ l² = 12² + 3.5² (putting the values)

⇒ l² = 144 + 12.25

⇒ l² = 156.25

⇒ l = √(156.25)

∴ l = 12.5 cm

C.S.A of cone = πrl

⇒ C.S.A of cone = π × 3.5 × 1.25 (putting the given values)

 ∴ C.S.A of cone = 43.75π m² ...(i)

C.S.A of hemisphere = 2πr²

⇒ C.S.A of hemisphere = 2 × π × 3.5²

= 2 × π × 12.25

= 24.5π m² ...(ii)

Now total surface area of toy = eqn1 + eqn2

⇒ Total surface area of toy = 43.75π + 24.5π

= 68.25π

⇒ The total surface area of toy = 68.25 × 22/7 (putting π = 22/7)

= 9.75 × 22

= 214.5 m²

The total surface area of the toy is 214.5 m².

36. If the radii of the circular ends of a bucket 28 cm high, are 28 cm and 7 cm, find its capacity and total surface area.

Solution

Explanation:

Here the bucket is in the shape of a frustum. So capacity of bucket will be equal to the volume of the frustum and in order to calculate the total surface area of the bucket we will subtract the top end circular area from the total surface area of the frustum as the bucket is open on top.

Upper end radius of frustum/bucket = R = 28 cm

Lower end radius of frustum/bucket = r = 7 cm

Height of the frustum/bucket = 28 cm

And we know,

The capacity of bucket = Volume of the bucket

And, Volume of bucket = Volume of Frustum

∴ Capacity of bucket = Volume of frustum

⇒ Volume of frustum = 1/3 × π × h × (r² + R² + (r × R))

Where R = Radius of larger or upper end and r = radius of smaller or lower end and h = height of frustum π = 22/7

⇒ Volume of frustum = 1/3 × 22/7 × 28 × (7² + 28² + (7 × 28))

= 22/3 × 4 × (49 + 784 + 196)

= 22/3 × 4 × 1029

= 22 × 4 × 343

∴ Volume of frustum = 30185 cm³

∴ Capacity of bucket = 30184 cm³

T.S.A of bucket = T.S.A of frustum – Area of upper circle ...(i)

Let the slant height of the frustum be ‘l’ cm

So, l² = h² + (R – r)²

⇒ l² = 28² + (28 – 7)²

⇒ l² = 784 + (21)²

⇒ l² = 784 + 441

⇒ l² = 1225

⇒ l = √(1225)

∴ l = 35 cm

⇒ T.S.A of frustum = π(R + r)l + πR² + πr²

= π(28 + 7) × 35 + π(28)² + π(7)²

= 35 × 35π + 784 π + 49 π

= 1225π + 784π + 49π ...(ii)

Area of upper circle = πR²

= π(28)²

= 784π ...(iii)

T.S.A of bucket = 1225 π + 784π + 49π - 784π (from eqn2 and 3)

⇒ T.S.A of bucket = 1274π

⇒ T.S.A of bucket = 1274 × 22/7 (putting π = 22/7)

⇒ T.S.A of bucket = 182 × 22

∴ T.S.A of bucket = 4004 cm²

The capacity and total surface area of the bucket is 30184 cm³ and 4004 cm².

37. A bucket is in the form of a frustum of cone with a capacity of 12308.8 cm3 of water. The radii of a cone with a capacity of 12308.8 cm3 of water. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket. (Use π= 3.14)

Solution

Upper end radius of frustum/bucket = R = 20 cm

Lower end radius of frustum/bucket = r = 12 cm

Height of the frustum/bucket be ‘h’ cm

And we know,

The capacity of bucket = Volume of the bucket

And, Volume of bucket = Volume of Frustum

Volume of frustum/bucket = V = 12308.8 cm³

∴ Capacity of bucket = Volume of frustum

⇒ Volume of frustum = V = 1/3 × π × h × (r² + R² + (r × R))

Where R = Radius of larger or upper end and r = Radius of smaller or lower end and h = height of frustum π = 3.14

⇒ 1/3 × π × h × (r² + R² + (r × R) = V

⇒ 1/3 × 3.14 × h × (122 + 202 + (12 × 20)) = 12308.8 (putting the values)

⇒ 3.14 × h × (144 + 400 + 240) = 12308.8 × 3

⇒ 3.14 × h × 784 = 36926.4

⇒ 2461.76 × h = 36926.4

⇒ h = 36926.4/2461.76

∴ h = 15 cm

The height of the bucket is 15 cm.

38. A milk container is made of metal sheet in the shape of frustum of a cone whose volume is 10459.3/7 cm³. The radii of its lower and upper circular ends are 8 cm and 20 cm respectively. Find the cost of metal sheet used in making the container at the rate of Rs 1.40 per cm².

Solution

Upper end radius of container = R = 20 cm

Lower end radius of container = r = 8 cm

Height of the container be ‘h’ cm

As container is in shape of frustum

Volume of container = Volume of Frustum

V = 10459.3/7 cm³

⇒ V = 73216/7 cm³

⇒ Volume of frustum = V = 1/3 × π × h × (r² + R² + (r × R))

where R = radius of larger or upper end

r = radius of smaller or lower end and,

h = height of frustum π = 22/7

⇒ 1/3 × π × h × (r² + R² + (r × R)) = V

⇒ 1/3 × 22/7 × h × (8² + 20² + (8 × 20)) = 73216/7 (putting the values)

⇒ 22/3 × h × (64 + 400 + 160) = 73216

⇒ 22 × h × 208 = 73216

⇒ 4576 × h = 73216

⇒ h = 73216/4576

∴ h = 16 cm

Let the slant height of the frustum be ‘l’ cm

So, l² = h² + (R – r)²

⇒ l² = 16² + (20 – 8)²

⇒ l2 = 256 + (12)²

⇒ l² = 256 + 144

⇒ l² = 400

⇒ l = √(400)

∴ l = 20 cm

Now the Area of sheet used in making the container can be calculated by simply subtracting by simple subtracting the area of the upper circular end from the T.S.A of frustum

⇒ T.S.A of frustum = π(R + r)l + πR² + πr²

= π(20 + 8) × 20 × π(20)² + π(8)²

= 28 × 20π + 400π + 64π

= 560π + 464π

= 1024π ...(i)

Area of upper circular end = πR²

= π(20)²

= 400π ...(ii)

T.S.A of container = 1024π - 400π (from eqn2 and 1)

⇒ T.S.A of container = 624π

= 13728/7 cm²

⇒ Cost of metal sheet used = T.S.A of container × Rate per cm²

⇒ Cost of metal sheet used = 13728/7 × 1.40

= 13728 × 0.2

= Rs 2745.6

The cost of the metal sheet used is Rs 2745.6

39. A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4.2/3 cm and height 3 cm. Find the number of cones so formed.

Solution

Explanation: Here the volume of all the resulting cones will be exactly equal to the volume of the sphere from which they area formed. Son we would find the volume of sphere and then divide the volume of sphere with the volume of one cones to find the number of cones formed.

Diameter of the sphere = D = 28 cm

Radius of the sphere = 28/2

Radius of the sphere = R = 14 cm

Volume of the sphere = V₁ = 4/3πR³ (put the value of R)

⇒ Volume of the sphere = V₁ = 4/3π(14)³

= (4π × 2744)/4

= 10976π/3 m³ ...(i)

Let the number of cones formed out of the sphere be ‘x’.

Diameter of each cone = 4.2/3 cm = 14/3 cm

Given the height of each cone = h = 3 cm

Then, radius

r = 14/3/2

r = 14/(3 × 2)

r = 7/3 cm

Volume of one cone = V₂ = 1/3π(r²)h

⇒ V₂ = 1/3 × π × (7/3)² × 3

⇒ V₂ = 49π/9 cm³ ...(ii)

Volume of ‘n’ number of cones = n × volume of one cone

Volumes of ‘m’ number of cones = volume of sphere

m × 49π/9 = 10976π/3

⇒ m = 49/3 = 10976

⇒ m = (10976 × 3)/49

⇒ m = 224 × 3

∴ m = 672

The number of cones formed out of the sphere is 672.

40. A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the volume (i) displaced out of the cylinder (ii) left in the cylinder.

Solution

Given internal diameter of cylinder = D = 10 cm

Internal radius of cylinder = R = D/2 = 10/2

Internal radius of cylinder = R = 5 cm

Height of cylinder = H = 10.5 cm

Diameter of solid cone = d = 7 cm

Radius of solid cone = r = d/2 = 7/2

Radius of solid cone = r = 3.5 cm

Height of cone = h = 6 cm

(i) Volume displaced out of cylinder

By Archimedes principle we can easily say that,

Volume displaced out of cylinder = Volume of the solid cone

Volume of cone = V₂ = 1/3π(r²)h

⇒ V₂ = 1/3 × π × (3.5)² × 6

⇒ V₂ = 22/7 × 12.25 × 2

⇒ V = 22 × 1.75 × 2

∴ V = 77 cm³

The volume displaced out of cylinder is 77 cm³.

(ii) Volume left in cylinder

Volume left in cylinder = Volume of cylinder – Volume displaced out

Volume of cylinder = π(R)²H

⇒ Volume of cylinder = π × (5)² × 10.5 (putting the given values)

⇒ Volume of cylinder = π × 25 × 10.5

⇒ Volume of cylinder = π × 262.5

⇒ Volume of cylinder = 22/7 × 262.5

⇒ Volume of cylinder = 22 × 37.5

 ∴ Volume of cylinder = 825 cm³ ...(i)

Volume left in cylinder = 825 – 77 (from eqn1 and (i))

∴ Volume left in cylinder = 748 cm³

The volume left in the cylinder is 748 cm³.