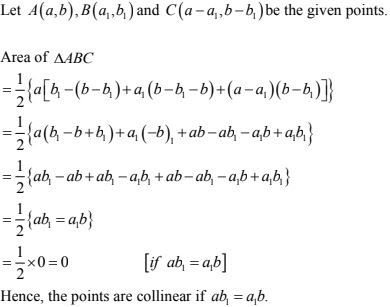Chapter 14 Co-Ordinate Geometry RD Sharma Solutions Exercise 14.5 Class 10 Maths

Chapter Name | RD Sharma Chapter 14 Co-Ordinate Geometry |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 14.5 Solutions
1. Find the area of a triangle whose vertices are
(i) (6, 3), (-3, 5) and (4, -2)
(ii) [(at21 , 2at1 ), (at22 , 2at2 ) (at23 , 2at3)]
(iii) (a, c + a), (a, c) and (-a, c- a)
Solution

2. Find the area of the quadrilaterals, the coordinates of whose vertices are
(i) (-3, 2), (5, 4), (7, -6) and (-5, -4)
(ii) (1, 2), (6, 2), (5, 3) and (3, 4)
(iii) (-4, -2), (-3, -5), (3, -2), (2, 3)
Solution


(iii)

3. The four vertices of a quadrilateral are (1, 2), (-5, 6), (7, -4) and (k, -2) taken in order. If the area of the quadrilateral is zero, find the value of k.
Solution

4. The vertices of ΔABC are (-2, 1), (5, 4) and (2, -3) respectively. Find the area of the triangle and the length of the altitude through A.
Solution

5. Show that the following sets of points are collinear.
(a) (2, 5), (4, 6) and (8, 8)
(b) (1, -1), (2, 1) and (4, 5)
(b) (1, -1), (2, 1) and (4, 5)
Solution
(a) Let A(2, 5), B(4, 6) and C(8, 8) be the given points
Area of ΔABC

6. Prove that the points (a, 0), (0, b) and (1, 1) are collinear if, 1/a + 1/b = 1.
Solution
Let A(a, 0), B(0, b) and C(1, 1) be the given points
Area of ΔABC

7. The point A divides the join of P (-5, 1) and Q (3, 5) in the ratio k : 1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, -2) is equal to 2 units.
Solution

8. The area of a triangle is 5. Two of its vertices are (2, 1) and (3, -2). Third vertex lies on y =
x + 3. Find the third vertex.
Solution

9. If a ≠ b ≠ c, prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
Solution
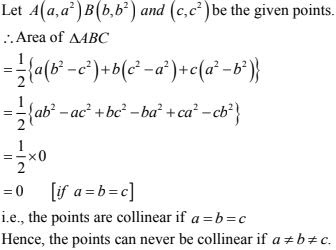
10. Four points A(6, 3), B(-3, 5), C(4, -2) and D(x, 3x) are given in such a way that ΔDBC/ΔABC = 1/2, find x.
Solution

11. For what value of a point (a, 1), (1, -1) and (11, 4) are collinear ?
Solution

Solution