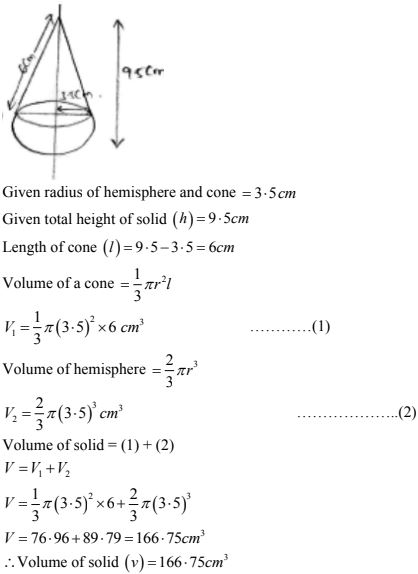RD Sharma Solutions for Class 10 Chapter 16 Surface Area and Volumes Exercise 16.2

Chapter 16 Surface Areas and Volumes RD Sharma Solutions Exercise 16.2 Class 10 Maths

Chapter Name	RD Sharma Chapter 16 Surface Area and Volumes Exercise 16.1
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 16.1 Exercise 16.3
Related Study	NCERT Solutions for Class 10 Maths

Exercise 16.2 Solutions

1. A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of

cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone

is 16 m above the ground. Find the area of canvas required for the tent.

Solution

Given diameter of cylinder 24m 

2. A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached tot the top. The cylinder is of radius 2.5m and height 21m and the cone has a a slant height 8m. Calculate total surface area and volume of the rocket ? 

Solution

Given radius of cylinder (a) = 2.5 m

Height of cylinder (h) = 21m 

Slant height of cylinder (l) = 8m 

3. A tent of height 77 dm is in the form of a right circular cylinder of diameter 36m and height 44 dm surmounted by a right circular cone. Find the cost of the canvas at Rs. 350/m² . (Use it 22/7)

Solution

4. A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of cone are 6cm and 4cm. determine surface area of toy ?

Solution

Given height of cone(h) = 4cm 

Diameter of cone (d) = 6cm 

∴ Radius (r) = 6/2 = 3 cm 

5. A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the heights of the cylindrical and conical portions are 10cm, and 6cm, respectively. Find the total surface area of the solid. (Use n = 22/7)

Solution

6 A cylindrical tube of radius 5cm and length 9.8cm is full of water. A solid in form of a right circular cone mounted on a hemisphere is immersed in tube. If radius of hemisphere is immersed in tube if the radius of hemisphere is 3.5cm and height of the cone outside hemisphere is 5cm. Find volume of water left in the tube?

Solution

Given radius of cylindrical tube (r) = 5cm. 

Height of cylindrical tube (h) = 9.8cm 

Volume of cylinder = πr² h

7. A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5cm and 13cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Find the surface area of the toy if the total height of the toy is 30 cm. 

Solution

8. A circular tent has cylindrical shape surmounted by a conical roof. The radius of cylindrical base is 20 m. The height of cylindrical and conical portions are 4.2m and 2.1m. Find the volume of the tent ?

Solution

Given radius of cylindrical base = 20m 
Height of cylindrical part (h) = 4.2m 

9. A petrol tank is a cylinder of base diameter 21cm and length 18cm fitted with conical ends each of axis 9cm. Determine capacity of the tank ? 

Solution

Given base diameter of cylinder = 21cm 

Radius (r) = 21/2 = 11.5cm 

Height of cylindrical part (h) = 18cm 

10. A conical hole is drilled in a circular cylinder of height 12cm and base radius 5cm. The height and base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder ? 

Solution

11. A tent is in form of a cylinder of diameter 20m and height 2.5m surmounted by a cone of equal base and height 7.5m. Find capacity of tent and cost of canvas at Rs 100 per square meter ? 

Solution

12. A boiler is in the form of a cylinder 2m long with hemispherical ends of 2m diameter. Find the volume of the boiler ? 

Solution

13. A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of cylinder is 14/3 m and internal surface area of the solid ? 

Solution

Given radius of hemisphere (r) = 3.5/2 = 1.75 m 
Height of cylinder (h) = 14/3 m 

14. A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104cm and radius of each of hemispherical ends is 7cm. Find the cost of polishing its surface at the rate of Rs 10 per dm²?

Solution

Given radius of hemispherical ends = 7cm 
Height of body (h + 2r) = 104cm. 

Curved surface area of cylinder = 2πrh 
= 2π(7)h ...(1)
⇒ 4 + 2x = 104
⇒ h = 104 - 2(r) 
⇒ h = 90cm 

Substitute 'h' value in (1) 
Curved surface area of cylinder = 2π(7)(90)  = 3960 cm² ...(2)
Curved surface area of 2 hemisphere = 2(2πr²)
= 2(2×π×7²) = 616 cm³ ...(3)
Total curved surface area (2) + (3) 
= 3960 + 616 =  4576 cm² = 45.76dm² 
Cost of polishing for 1dm² = Rs 10 
Cost of polishing for 45.76 dm² = 45.76 ×10 = Rs 457.6 

15. A cylindrical vessel of diameter 14cm and height 42cm is fixed symmetrically inside a similar vessel of diameter 16cm and height 42cm. The total space between two vessels is filled with cork dust for heat insulation purpose. How many cubic cms of cork dust will be required ? 

Solution

Given height of cylindrical vessel (h) = 42cm 

16. A cylindrical road solar made of iron is 1m long its internal diameter is 54cm and thickness of the iron sheet used in making roller is 9cm. Find the mass of roller if 1cm³  of iron has 7.8 gm mas ?

Solution

17. A vessel in from of a hollow hemisphere mounted by a hollow cylinder. The diameter of hemisphere is 14cm and total height of vessel is 13cm. Find the inner surface area of vessel ? 

Solution

Given radius of hemisphere and cylinder (r) = 14/2 = 7cm 

Given total height of vessel  = 13cm 

(h + r) = 13cm 

Inner surface area of vessel = 2πr(h + r) 
= 2 × π × 7 (13) 
= 182 π
= 572 cm²  

18. A toy is in the form of a cone of radius 3.5cm mounted on a hemisphere of same radius. The total height of toy is 15.5cm. Find the total surface area of toy ? 

Solution

19. The difference between outside and inside surface areas of cylindrical metallic pipe 14cm long is 44m². If pipe is made of 99 cm³ of  metal. Find outer and inner radii of pipe?

Solution

We have to find the outer and inner radius of a hollow pipe.

Radius of inner pipe be(r₁)

Radius of outer cylinder be (r₂)

Length of the cylinder(h) = 14 cm 

Difference between the outer and the inner surface area is 44 cm²

So,

2πh(r₂ - r₁) = 44

inner pipe radius (r₁): 2 cm

outer cylinder (r₂): 2.5 cm

20. A radius circular cylinder bring having diameter 12cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6cm having a hemisphere shape on top find the number of such cones which can be filled with ice-cream? 

Solution

We have,

Radius of the cylincler = 12/2 = 6cm

Height of the cylinder = 15cm

∴ volume of the cylinder = πr²h

 = π× 6² ×15

= 540πcm³

Radius of the ice-cream cone = 3cm

Height of the ice-cream cone = 12cm

∴ volume of the conical part of ice-cream

21. A solid iron pole having cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole given that the mass of 1 cm³ of iron is 8gm ? 

Solution

Given radius of cylindrical part (r) = 12/2 = 6 cm 

Height of cylinder (h) = 110 cm 

Length of cone (l) = 9cm 

Volume of cylinder  = πr² h 

22. A solid toy is in the form of a hemisphere surmounted by a right circular cone. Height of the cone is 2cm and the diameter of the base is 4cm. If a right circular cylinder circumscribes the toy find how much more space it will cover. 

Solution

Given radius of cone, cylinder and hemisphere (r) = 4/2 = 2cm 

Height of cone (l) = 2cm 

Height of cylinder (h) = 4cm 

Volume of cylinder = πr² h = π(2)² (4) cm³ ...(1)

23. A solid consisting of a right circular cone of height 120 cm and radius 60 cm is placed upright in right circular cylinder full of water such that it touches bottoms. Find the volume of water left in the cylinder. If radius of cylinder is 60cm and its height is 180 cm ? 

Solution

Given radius of circular cone (a) = 60cm 

Height of circular cone (b) = 120 cm. 

24. A cylindrical vessel with internal diameter 10cm and height 10.5cm is full of water. A solid cone of base diameter 7cm and height 6cm is completely immersed in water. Find value of water (i) displaced out of the cylinder

(ii) left in the cylinder ? 

Solution

25. A cylindrical vessel with internal diameter 10 cm and height 10.5cm is full of water. A solid cone of base diameter 7cm and height 6cm is completely immersed in water. Find value of water (i) displaced out of the cylinder (ii) left in the cylinder?

Solution

26. A hemispherical depression is cut from one face of a cubical wooden block of edge 21cm such that the diameter of hemisphere is equal to the edge of cube determine the volume and total surface area of the remaining block ? 

Solution

Given edge of wooden block (a) = 21cm 

Given diameter of hemisphere = edge of cube 

Radius = 21/2 = 10.5cm 

Volume of remaining block = volume of box - volume of hemisphere 

27. A tag is in the form of a hemisphere surmounted by a right circular cone of same base radius as that of the hemisphere. If the radius of the base of cone is 21 cm and its volume is 2/3 of  volume of hemisphere calculate height of cone and surface area of toy ? 

Solution

28. A solid is in the shape of a cone surmounted on hemisphere the radius of each of them is being 3.5 cm and total height of solid 9.5 cm. Find  volume of the solid ? 

Solution