RS Aggarwal Class 10 Solutions Chapter 18 Areas of Circle, Sector & Segment Exercise 18B

Chapter 18 Areas of Circle, Sector & Segment RS Aggarwal Solutions Exercise 18B Class 10 Maths

Chapter Name	RS Aggarwal Chapter 18 Areas of Circle, Sector & Segment
Book Name	RS Aggarwal Mathematics for Class 10
Other Exercises	Exercise 18A MCQ
Related Study	NCERT Solutions for Class 10 Maths

Areas of Circle, Sector & Segment Exercise 18B Solutions

1. The circumference of a circle is 39.6 cm. Find its area.

Solution

In order to solve such type of questions we basically need to find the radius of the give circle and simply use it to find the area of the given circle.

Given the circumference of perimeter of the circle = 39.6 cm.

And we know, Perimeter or circumference of circle = 2πr

Where, r = Radius of the circle

Therefore, 2πr = 39.6

⇒ r = 39.6/2π

(Put value of π = 22/7)

⇒ r = 39.6/(2 × 22/7)

On rearranging we get,

⇒ r = (39.6 × 7)/(2 × 22)

⇒ r = 277.2/44

⇒ r = 6.3 cm

So, the radius of the circle = 6.3 cm

And we also know, Area of the circle = πr²

Where, r = radius of the circle

⇒ Area of the circle = π(6.3)²

(putting value of r)

= 22/7(6.3²)

= 22/7 (6.3 × 6.3)

= 22/7 × 39.69

= 22 × 5.67

= 124.74 cm²

The area of the circle = 124.74 cm².

2. The area of the circle is 98.56 cm². Find its circumference.

Solution

In order to solve such type of questions we basically need to find the radius of the give circle and simply use it to find the circumference or perimeter of the given circle.

Given the area of the circle = 98.56 cm²

 And we know, Area of the circle = πr²

Therefore, πr² = 98.56

⇒ r² = 98.56/π

(put value of π = 22/7)

⇒ r² = 98.56/(22/7)

On rearranging we get,

⇒ r² = (98.56 × 7)/22

⇒ r² = (689.22)/22

⇒ r² = 31.36

⇒ r = √31.36

⇒ r = 5.6 cm

So, the radius of the circle = 5.6 cm

And we know, Perimeter of circle = 2πr

(put value of r)

⇒ Circumference or Perimeter of circle = 2π(5.6)

= 2 × 22/7 × 5.6 (put π = 22/7)

= (2 × 22 × 5.6)/7

= (246.4)/7

= 35.2 cm

The circumference or perimeter of the circle is 35.2 cm.

3. The circumference of a circle exceeds its diameter by 45 cm. Find the circumference of the circle.

Solution

Given, the circumference of a circle exceeds its diameter by 45 cm.

⇒ Circumference of circle = Diameter of circle + 45

Let ‘d’ = diameter of the circle

⇒ Circumference = d + 45 ...(i)

And we know, Circumference of circle = 2 πr ...(ii)

Where r = radius of circle

Also, we know that the radius of the circle is half of its diameter.

⇒ r = d/2 ...(iii)

Put value of circumference in equation 1 from equation 2

⇒ 2πr = d + 45 ...(iv)

Put value of r in equation 4 from equation 3

⇒ 2π(d/2) = d + 45

⇒ πd = d + 45

⇒ πd – d = 45

⇒ (π – 1)d = 45 (taking d common from L.H.S)

⇒ d = 45/(π – 1) (now put π = 22/7)

⇒ d = 45/(22/7 – 1)

⇒ d = {45/(22 – 7)/7} (taking 7 as LCM in denominator)

⇒ d = 45/(15/7)

On rearranging, we get

⇒ d = (45 × 7)/15

⇒ d = 315/15

⇒ d = 21 cm

Therefore, the diameter of the circle is 21 cm.

Thus, the radius of the circle r = d/2 (from equation 3)

∴ r = 21/2

⇒ r = 10.5 cm

Now put the value of r in equation 2, we get

⇒ Circumference or Perimeter of circle = 2π(10.5) (put π = 22/7)

= 2 × 22/7 × 10.5

= (2 × 22 × 10.5)/7

= 462/7

= 66 cm

The circumference of the circle is 66 cm.

4. A copper wire when bent in the form of a square encloses an area of 484 cm². The same wire is now bent in the form of a circle. Find the area enclosed by the circle.

Solution

In this question the wire is first bent in the shape of square and then same wire is bent to form a circle. The point to be noticed is that the same wire is used both the times which implies that the perimeter of square and that of circle will be equal.

Let the square be of side ‘a’ cm and radius of the circle be ‘r’.

Given the area enclosed by the square = 484 cm²

Also, we know that area of square = Side × Side

Area of the square = a²

⇒ a² = 484

⇒ a = √484

⇒ a = 22 cm

Therefore, side of square, ‘a’ is 22 cm.

Also, circumference of the circle = Perimeter of square ...(i)

Perimeter of square = 4 × side

Perimeter of square = 4 × 22

⇒ Perimeter of square = 88 cm ...(ii)

Also, we know, Circumference of circle = 2πr ...(iii)

Put values in equation 1 from equation 2 & 3, we get

2πr = 88

⇒ r = 88/2π (put π = 22/7)

⇒ r = 88/(2 × 22/7)

On rearranging,

⇒ r = (88 × 7)/(2 × 22)

⇒ r = 616/44

⇒ r = 14 cm

So, the radius ‘r’ of the circle is 14 cm.

Area of circle = πr²

where r = radius of the circle

= π(14)²

= (22/7 × 14 × 14) (put π = 22/7)

= (22 × 14 × 14)/7

= 4312/7

= 616 cm²

Area of the circle is 616 cm².

5. A wire when bent in the form of an equilateral triangle encloses an area of 121√3 cm². The same wire is bent to form a circle. Find the area enclosed by the circle.

Solution

In this question the wire is first bent in the shape of equilateral triangle and then same wire is bent to form a circle. The point to be noticed is that the same wire is used both the times which implies that the perimeter of equilateral triangle and that of circle will be equal.

Let the equilateral triangle be of side ‘a’ cm and radius of the circle be ‘r’.

Given: Area enclosed by equilateral triangle = 123√3 cm²

Also, we know that Area of equilateral triangle = √3/4 a²

Where ’a’ = side of equilateral triangle

⇒ √3/4.a² = 121√3

⇒ a² = 121√3/(√3/4)

⇒ a² = (121√3 × 4)/ √3

⇒ a² = (484√3)/ √3

⇒ a = √484

⇒ a = 22 cm

Therefore, side of equilateral triangle, ‘a’ is 22 cm.

Also, circumference of the circle = Perimeter of equilateral triangle ...(i)

Perimeter of equilateral triangle = 3 × side

= 3 × 22

= 66 cm ...(ii)

Also, we know Circumference of circle = 2πr ...(iii)

Put values in equation 1 from equation 2 & 3, we get

2πr = 66

⇒ r = 66/2π

(put π = 22/7)

⇒ r = 66/(2 × 22/7)

On rearranging,

⇒ r = (66 × 7)/(2 × 22)

⇒ r = 462/44

⇒ r = 10.5 cm

So, the radius ‘r’ of the circle is 10.5 cm.

Area of circle = πr²

6. The length of a chain used as the boundary of a semi-circular park is 108 m. Find the area of the park.

Solution

In this equation the length of chain used as boundary of the semi-circular park is the perimeter of the semi-circular park. By using this we will first calculate the radius of the semi-circular park and then area of semicircle consequently.

Length of chain = 108 m

Length of chain = Perimeter or circumference of semicircle

Therefore, Circumference or Perimeter of semicircle = 108 m

Therefore, Circumference or Perimeter of semi-circle = πr

Where r = radius of semicircle

⇒ πr = 108

⇒ r = 108/π

(put π = 22/7)

⇒ r = 108/(22/7)

On rearranging,

⇒ r = (108 × 7)/22

⇒ r = 756/22

⇒ r = 34.46 m

Therefore, radius of semicircle is 34.36 m.

As, area of semicircle = πr²/2 ...(i)

Put value of ‘r’ in equation 1, we get

Area of semicircle = π(34.36²)/2

(put π = 22/7)

= (22/7 × 34.36 × 34.36)/2

On rearranging,

= (22/ × 34.3636 × 34.3636)/(7 × 2)

= (25973.4112)/14

= 1855.63 m²

The area of the semi-circular park is 1855.63 m².

7. The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumferences of the circles.

Solution

Given sum of the radius of the circles = 7 cm

The difference of their circumference = 8 cm

Let the radius one circle be ‘r₁’ cm and other be ‘r₂’ cm and circumference be ‘C₁’ and ‘C₂’ respectively.

Also, circumference of circle = 2πr

Where r = radius of the circle

C₁ = 2πr₁ and C₂ = 2πr₂

r₁ + r₂ = 7 ...(i)

C₁ – C₂ = 8 ...(ii)

(Note: Her it is considered that r₁ > r₂)

We can rewrite equation 2 as,

2πr₁ - 2πr₂ = 8

⇒ 2π (r₁ – r₂) = 8

(taking 2π common from L.H.S)

⇒ r₁ – r₂ = 8/2π – eqn3

⇒ r₁ – r₂ = 8/(2 × 22/7)

⇒ r₁ – r₂ = (8 × 7)/44

⇒ r₁ – r₂ = 56/44

⇒ r₁ – r₂ = 14/11

⇒ r₁ = 14/11 + r₂ ...(iii)

Put the value of r1 from equation 3 in equation 1

14/11 + r₂ + r₂ = 7

⇒ 14/11 + 2r₂ = 7

⇒ 2r₂ = 7 – 14/11

⇒ 2r₂ = (77 – 14)/11

(taking 11 as LCM on R.H.S)

⇒ 2r₂ = 63/11

⇒ r₂ = 63/(2 × 11)

⇒ r₂ = 63/22 cm

Put value of r₂ in equation 3

∴ r₁ = 14/11 + 63/22 (from equation 3)

⇒ r₁ = (28 + 63)/22 (taking 22 as LCM on R.H.S.)

⇒ r₁ = 91/22 cm

∴ C₁ = 2π (91/22) (by putting value of r₁)

⇒ C₁ = 2 × 22/7 × 91/22

= (2 × 22 × 91)/(7 × 22)

= (2 × 91)/7

= 182/7

= 26 cm

C₂ = 2π (66/22) (by putting value of r₂)

⇒ C₁ = 2 × 22/7 × 63/22

= (2 × 22 × 63)/(7 × 22)

= (2 × 63)/7

= 126/7

= 18 cm

The circumference of circles are 26 cm and 18 cm.

8. Find the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.

Solution

Consider the ring as shown in the figure below:

The inner radius of ring is ‘r’ and the outer radius is ‘R’.

Area of circle = πr² and Area of outer circle = πR²

Where r = 12 cm and R = 23 cm

Area of ring = Area of outer circle – Area of inner circle

Area of ring = πR² – πr² (put values of r & R)

⇒ Area of ring = π(23²) – π(12²)

⇒ Area of ring = π(23² – 12²) (taking π common from R.H.S)

⇒ Area of ring = π(529 – 144)

= (22 × 385)/7

= 8470/7

= 1210 cm²

Area of ring is 1210 cm²

9. A path of 8 m width runs around the outside of a circular park whose radius is 17 m. Find the area of the path.

Solution

Given radius of circular park = R = 17 m

Width of the circular path outside the park = d = 8 m

Therefore, the radius of the outer circle = R’ = R + d

Outer radius = R’ = 17 + 8

R’ = 25 m

Area of inner circle = πR² and,

Area of outer circle = πR’²

Area of path = Area of outer circle = Area of inner circle

= πR’² – πr² (put values of R & R')

= π(25²) – π(17²)

= π(25² – 17²) (taking π common from R.H.S)

= π(625 – 289)

⇒ Area of path = 22/7 × 336

(put π = 22/7)

= 7392/7

= 1056 m²

The area of the path is 1056 m².

10. A racetrack in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.

Solution

Consider the race track as shown below,

The inner and outer radius of track is ‘r’ cm and ‘R’ cm respectively.

Let inner and outer circumference be ‘C₁’ and C₂’ respectively.

C₁ = 352 m and C₂ = 396 m

We know,

Circumference of circle = 2πr

Where r = radius of the circle

C₁ = 2πr and C₂ = 2πR

⇒ 2πr = 352 and 2πR = 396

⇒ r = 352/2π and R = 396/2π (put π = 22/7)

⇒ r = 352/(2 × 22/7) and R = 396/(2 × 22/7)

On rearranging,

⇒ r = (352 × 7)/(2 ×22) and R = (396 × 7)/(22 × 22)

⇒ r = 2464/44 and R = 2772/44

⇒ r = 56 m and R = 63 m

So, the width of the race track = R – r,

⇒ Width of the race track = 63 - 56,

⇒ Width of the race track = 7 m

Area of race track = area of outer circle – area of inner circle

⇒ Area of track = πR² – πr² (put values of r and R)

⇒ Area of track = π(63)² – π(56²)

⇒Area of track = π(63)² – (56)² (taking π common from R.H.S)

⇒ Area of track = π(3969 – 3136)

⇒ Area of track = π × 833

⇒ Area of track = 22/7 × 833 (put π = 22/7)

= 22 × 119

= 2618 m²

The width of track in 7 m and area of track is 2618 m².

11. A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the angle of the arc and the area of the sector.

Solution

Consider the circle shown above,

Given radius of the circle = R = 21 cm ...(i)

And angle of the sector = θ = 150° ...(ii)

Length of arc of a sector = θ/360 × 2πR ...(iii)

Where ‘R’ =radius of sector (or circle)

θ = Angle subtended by the arc on the centre of the circle

Put the values of R and θ from equation 1 and 2 in equation 3

⇒ Length of arc = 150/360 × 2π(21) (put π = 22/7)

= 150/360 × 2 × 22/7 × 21

= (150 × 2 × 22 × 21)/(360 × 7)

= 138600/2520

= 55 cm

Area of a sector = θ/360 × πR² ...(iv)

Where ‘R’ = radius of sector (or circle)

θ = angle subtended by the arc on the centre of the circle

Put the values of R and θ from equation 1 and 2 in equation 3

⇒ Area of sector = 150/360 × π(212) (put π = 22/7)

= (150 × 22 × 22 × 21)/(360 × 7)

= 1455300/2520

= 577.5 cm²

The length of arc is 55 cm and area of sector is 577.5 cm².

12. The area of the sector of a circle of radius 10.5 cm is 69.3 cm². Find the central angle of the sector.

Solution

Consider the circle shown above,

We know, Area of sector = θ/360 × πR² ...(i)

Where R = radius of the circle and θ = central angle

Given R = 10.5 cm and Area of sector = 69.3 cm²

Let the angle subtended at centre = θ

Put the values of R and area of sector in equation 1

⇒ 69.3 = θ/360 × π(10.5²) (put π = 22/7)

⇒ 69.3 = θ/360 × 22/7 × 10.5 × 10.5

⇒ 69.3 = (θ × 22 × 10.5 × 10.5)/(360 × 7)

⇒ 69.3 = (θ × 2425.5)/2520

⇒ (69.3 × 2520)/2425.5 = θ

⇒ 174636/2424.5 = θ

⇒ θ = 72°

The central angle of the sector is 72°.

13. The length of an arc of a circle, subtending an angle of 54° at the centre is 16.5 cm. Calculate the radius, circumference and area of the circle.

Solution

Consider the circle shown above,

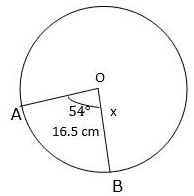
We know, Length of arc of sector = θ/360 × 2πR ...(i)

Where R = radius of circle and θ = central angle of the sector

Given, Length of arc = l = 16.5 and θ = 54°.

Let the radius be x cm

Put the values of l and θ in equation 1

⇒ 16.5 = 54/360 × 2πx (put π = 22/7)

⇒ 16.5 = (54 × 2 × 22 × x)/(360 × 7)

⇒ 16.5 = (2376 × x)/2520

On rearranging

⇒ (16.5 × 2520)/2376 = x

⇒ 41580/2376 = x

⇒ x = 17.5 cm

Also, we know circumference of the circle = 2πR

⇒ Circumference of the circle = 2πx (put value of x in this equation)

⇒ Circumference of the circle = 2π(17.5)

⇒ Circumference of the circle = 2 × 22/7 × 17.5 (put π = 22/7)

= (2 × 22 × 17.5)/7

= 770/7

Circumference of the circle = 110 cm

Also, we know Area of the circle = πR²

⇒ Area of the circle = πx²

⇒ Area of the circle = π(17.5²)

⇒ Area of the circle = 22/7 × 17.5 × 17.5 (put π = 22/7)

⇒ Area of the circle = (22 × 17.5 × 17.5)/7

⇒ Area of the circle = 6737.5/7

⇒ Area of the circle = 962.5 cm²

The radius of circle is 17.5 cm, circumference is 110 cm and area is 962.5 cm²

14. The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.

Solution

Consider the above figure,

From here we can conclude that the portion or the segment below the chord AB is the minor segment and the segment above AB is major segment.

Also we know,

Area of minor segment = Area of sector – Area of △AOB ...(i)

Now, Area of sector = θ/360 × πR² ...(ii)

Where R = radius of the circle and θ = central angle of the sector

Given, R = 7 cm and θ = 90°

Putting these values in the equation 2, we get

Area of sector = 90/360 × π(7)² (put π = 22/7)

= 90/360 × 22/7 × 7 × 7

= (90 × 22 × 7 × 7)/(360 × 7)

= 97020/2520

⇒ Area of sector = 38.5 cm² ...(iii)

Area of △AOB = 1/2 × base × height

NOTE : In gene Area of △AOB = 1/2 × OA × OB × sin θ

As triangle is isosceles therefore height and base both are 7 cm.

⇒ Area of △AOB = 1/2 × 7 × 7 = 49/2

= 24.5 cm² ...(iv)

Putting values of equation 2 and 4 in equation 1 we get

Area of minor segment = 38.5 – 24.5

⇒ Area of minor segment = 14 cm²

Area of major segment = πR² – Area of minor segment = eqn5

Put the value of R, and Area of minor segment in equation 5 = π(7²) – 14

= 49π – 14

⇒ Area of major segment = 22/7 × 49 – 14 (put π = 22/7)

= (22 × 7) – 14

= 154 – 14

= 140 cm²

Area of minor segment is 14 cm² and of major segment is 130 cm².

15. Find the lengths of the arcs cut off from a circle of radius 12 cm by a chord 12 cm long. Also, find the area of the minor segment.[Take π = 3.14 and = 1.73.].

Solution

Consider the figure shown above.

In this, the triangle AOB is an equilateral triangle as all the sides are equal; therefore it is obvious that the central angle of the sector is 60 degrees. Now by simply applying the formula of length of an arc, we can easily calculate the length of arc of the sector AOB.

Given radius of circle = R = 12 cm,

Length of chord AB = 12 cm

∴ Central angle = θ = 60°  (∵ △AOB is an equilateral triangle)

Length of arc = θ/360 × 2π(R) ...(i)

Where R = radius of circle and θ = central angle of the sector

Put the values of R and θ in equation 1

⇒ Length of minor arc = 60/360 × 2π(12) (put π = 3.14)

= 60/360 × 2 × 3.14 × 12

= (60 × 2 × 3.14 × 12)/360

= (2 × 3.14 × 12)/6

= 2 × 3.14 × 2

= 12.56 cm

Now, Length of major arc = 2πR – Length of minor arc

⇒ Length of major arc = 2π(12) – 12.56 (put π = 3.14)

⇒ Length of major arc = (2 × 3.14 × 12) – 12.56 

⇒ Length of major arc = 75.36 – 12.56

⇒ Length of major arc = 62.8 cm

Now, area of minor segment = Area of sector – Area of triangle ...(i)

∴ Area of sector = θ/360 × πr² (put the values of R and θ)

= 60/360 × π(12²)

= 60/360 × 3.14 × 144

= 75.36 cm² -eqn2

Area of triangle = √3/4 × a² (put a = 12 cm)

= √3/4 × (12²)

⇒ Area of triangle = √3/4 × 144

⇒ Area of triangle = 1.73 × 36

⇒ Area of triangle = 62.28 cm² -eqn3

Put the values of equation 2 and 3 in equation 1,

∴ Area of minor segment = 75.36 – 62.28

= 13.08 cm²

Length of major arc is 62.8 cm and minor arc is 12.56 cm and area of minor arc is 12.56 cm and area of minor segment is 13.08 cm².

16. A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the areas of both the segments . [Take π = 3.14].

Solution

Consider the figure shown above.

In this, the triangle AOB is an isosceles triangle. So here we will construct a perpendicular bisector from O on AB and as this triangle is isosceles therefore this perpendicular will also act as median and angle bisector.

Therefore,

Draw a perpendicular bisector from O which meets AB at D and bisects AB, as ABO is an isosceles triangle therefore OD acts as a median.

So, consider right angle triangle AOD right angled at D

sin θ = Perpendicular/Hypotenuse

Let ∠AOD = θ ⇒ Perpendicular = AD and Hypotenuse = AO = R

Given Radius of circle = R = 5√2 cm

Length of chord AB = 10 cm, AD = 5 cm

sin θ = AD/AO (put values of AD and AO)

⇒ sin θ = 5/5√2 = 1/√2

⇒ sin θ = sin 45°

 (as sin 45° = 1/√2)

⇒ θ = 45°

∴ ∠AOD = 45°

Thus we can say ∠AOB = 90° (As ∠AOD = 1/2∠AOB)

Area of minor segment = Area of sector – Area of right angle triangle ...(i)

Area of sector = θ/360 × πR²

Where R = radius of the circle and θ = central angle of the sector

Area of sector = 90/360 × π((5√2)²) (put π= 3.14)

= 90/360 × 3.14 × 50

= (3.14 × 50)/4

∴ Area of sector = 39.25 cm²

Area of right angle triangle = 1/2 × base × height

As this is isosceles right-angle triangle

∴ Height = base = 5√2 cm

Area of right angle triangle = 1/2 × 5√2 × 5√2 = 50/2 = 25 cm²

Put the value of area of sector and area of right angle triangle in equation 1,

⇒ Area of minor segment = 39.25 – 25

= 14.25 cm²

Area of major segment = πR² – area of minor segment

Area of major segment = π((5√2)²) – 14.25

= 3.14 × 5√2 × 5√2 – 14.25

⇒ Area of major segment = 157 – 14.25 = 142.75 cm²

Area of major segment is 142.75 cm² and of minor segment is 14.25 cm².

17. Find the area of both the segments of a circle of radius 42 cm with central angle 120°. [Given, sin 120° - √3/2 and √3 = 1.73]

Solution

Given R = 42 cm and central angle of sector = 120°

Area of minor segment = Area of sector – Area of triangle ...(i)

Area of sector = θ/360 × πR²

Where R = radius of the circle and θ = central angle of the sector

Area of sector = 120/360 × π(42²) (put π = 22/7)

= 120/360 × 22/7 × 1764

∴ Area of sector = 1848 cm²

Area of right angle triangle = 1/2 × base × height × sin θ

Where θ = central angle of the sector

Area of triangle = 1/2 × 42 × 42 × sin 120°

(put the value sin 120° = √3/2)

Area of triangle = 1/2 × 42 × 42 × √3/2

Area of triangle = (42 × 42 × √3)/4

(put √3 = 1.73)

Area of triangle = (42 × 42 × 1.73)/4

= 762.93 cm²

Put the values of area of triangle and area of sector in equation 1

⇒ Area of minor segment = 1848 – 762.93

= 1085.07 cm²

Area of major segment = πR² – Area of minor segment

Put the value of area of minor segment and R in above equation

= π(42²) – 1085.07

⇒ Area of major segment = 22/7 × 42 × 42 – 1085.07 (put π = 22/7)

⇒ Area of major segment = 5544 – 1085.07

∴ Area of major segment = 4458.93 cm²

Area of major segment is 4458.93  cm² and of minor segment is 1085.07 cm².

18. A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor and major segments. [Take π = 3.14 and √3 = 1.732]

Solution

Area of minor segment = Area of sector – Area of triangle ...(i)

Area of sector = θ/360 × πR²)

Where R = radius of the circle and θ = central angle of the sector

Area of sector = 60/360 × π(30²) (put π = 3.14)

Area of sector = 60/360 × 3.14 × 900

Area of sector = (3.14 × 900)/6

∴ Area of sector = 471 cm²

Area of right angle triangle = √3/4 × a²

Where a = side of the triangle

Area of triangle = √3/4 × 30 × 30

Area of triangle = √3/4 × 900

Area of triangle = (900 × (√3))/4

(put √3 = 1.732)

Area of triangle = (1.732 × 900)/4

∴ Area of triangle = 389.7 cm²

Put the values of area of triangle and area of sector in equation 1

Area of minor segment = 471 – 389.7

⇒ Area of minor segment = 81.3 cm²

Area of major segment = πR² – Area of minor segment

Put the value of area of minor segment and R in above equation

⇒ Area of major segment = π × (30²) – 81.3 (put π = 3.14)

⇒ Area of major segment = 3.14 × 30 × 30 - 81.3

⇒ Area of major segment = 2826 – 81.3

 = 2744.7 cm²

Area of major segment is 2744.7 cm² and of minor segment is 81.3 cm².

19. In a circle of radius 10.5 cm, the minor arc is one-fifth of the major arc. Find the area of the sector corresponding to the major arc.

Solution

Given radius of circle = R = 10.5 cm

Let the area of major sector be ‘A₁’ and that of minor sector be ‘A₂’.

∴ A₂ = A₁/5 ...(i)

We know, Area of circle = Area of major sector + Area of minor sector

⇒ Area of circle = A₁ + A₂

⇒ Area of circle = A₁ + A₁/5 ...(ii) (from equation 1)

We also know, Area of circle = πR²

Where R = radius of circle, put value of area of circle in equation 2.

⇒ π(10.5²) = (5A₁ + A₁)/5

(taking 5 as L.C.M. on R.H.S)

⇒ π × 10.5 × 10.5 = 6A₁/5

⇒ 22/7 × 10.5 × 10.5 = 6A₁/5

⇒ (22 × 10.5 × 10.5)/7 = 6A₁/5

⇒ 22 × 10.5 × 1.5 = 6A1/5

⇒ 346.5 = 6A₁/5

⇒ (5 × 346.5)/6 = A₁

= 288.75 cm²

The area of major sector is 288.75 cm².

20. The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days. [Take π = 3.14]

Solution

In an hour the minute hand completes one rotation therefore in 24 hours the minute hand will complete 24 rotations similarly the hour hand completes one rotation in 12 hours therefore in 24 hours it will complete 2 rotations. Now we have to just calculate the perimeter of the circle traced by minute hand and hour hand and multiply it with the number of rotations of minute hand and hour in 2 days respectively.

Length of short/hour hand = r = 4 cm

Length of long/minute hand = R = 6 cm

∴ The perimeter of circle traced by short hand = p = 2πr ...(i)

∴ The perimeter of circle traced by long hand = P = 2πR ...(ii)

Now put the value of ‘r’ and ‘R’ in the equation 1 and 2 respectively.

⇒ p = 2π(4) & P = 2 π(6) (put π = 3.14)

⇒ p = 2 × 3.14 × 4 & P = 2 × 3.14 × 6

∴ p = 25.12 cm & P = 37.68 cm

Therefore, distance covered by short hand in one rotation = 25.12 cm

Distance covered by long and in one rotation = 37.68 cm

Number of rotation of short hand in one day = 2

Number of rotation of long hand in on day = 24

Therefore number of rotation of small hand in two days = 4

Number of rotation of long hand in two days = 48

Total distance covered by long hand in 2 days = P × no. of rotations in 2 days

⇒ Total distance covered by long hand in 2 days = 37.68 × 48

⇒ Total distance covered by long hand in 2 days = 1808.64 cm ...(iii)

Total distance covered by short hand in 2 days = p × no. of rotations in 2 days

⇒ Total distance covered by short hand in 2 days = 25.12 × 24

⇒ Total distance covered by short hand in 2 days = 100.48 cm ...(iv)

Now, total distance covered by tip of both hands in 2 days = eqn3 + eqn4

⇒ Total distance covered by both hands in 2 days = 1808.64 + 100.48

⇒ Total distance covered by both hands in 2 days = 1909.12 cm

The distance covered by both hands in 2 days is 1909.12 cm

21. Find the area of a quadrant of a circle whose circumference is 88 cm.

Solution

Quadrant is a sector in which the central angle is 90 degrees, and this is the key to solve this question, As we know the central angle of the sector so we can easily calculate the area of quadrant by first calculating the radius of the circle as the circumference of the circle is given and then applying the formula of area of sector.

So, we know Circumference of a circle = 2πR – eqn1

Where R = radius of the circle

Given Circumference of the circle = 88 cm, θ = 90°

Put the given values in equation 1

88 = 2 × 22/7 × R (π = 22/7)

⇒ 88 = (2 × 22 × R)/7

⇒ 88 = (44 × R)/7

⇒ 88 = 44R/7

⇒ (88 × 7)/44 = R

⇒ 616/44 = R

⇒ R = 14 cm

Now we know, Area of a sector = θ/360 × πR²

Put the values of R and θ in the above equation

⇒ Area of quadrant = 90/360 × π(14²)

= 90/360 × 22/7 × 14 × 14

= (90 × 22 × 14 × 14)/(360 × 7)

= (22 × 14 × 14)/(4 × 7)

= 4312/28

= 154 cm2

The area of quadrant is 154 cm².

22. A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now to graze?

Solution

Here the increase in the length of the rope simply means that there is increase in the radius of the circle within which cow can graze. Now find the additional area available for grazing can be easily be found by simply subtracting the initial area available for grazing from the new area available.

Initial radius = r = 16 cm

Increased radius = R = 23 cm

Additional ground available = Area of new ground – Initial area ...(i)

Initial area of ground = π(r²)

⇒ Initial area of ground = π(16²)

⇒ Initial area of ground = 256π ...(ii)

Area of new ground = πR²

⇒ Area of new ground = π(23²)

⇒ Area of new ground = 529π ...(iii)

Now put the values of equation 2 and 3 in equation 1

⇒ Additional area of ground available = 529π - 256π

⇒ Additional area available 529π - 256π

⇒ Additional area available = (529 – 256)π (Taking π common)

⇒ Additional ground available = 273π

⇒ Additional ground available = 273 × 22/7 (put π = 22/7)

= (22 × 273)/7

= 6006/7

= 858 cm²

The additional ground available is 858 cm².

23. A horse is placed for grazing inside a rectangular field 70 m by 52 m. It is tethered to one corner by a rope 21 m long. On how much area can it graze? How much area is left ungrazed ?

Solution

Here the horse is tethered to one corner implies or means that the area available for grazing is a quadrant of radius 21 m. Now we need to find the area of this quadrant to find out the area available for grazing and then subtract it from the total area of the rectangular field to obtain the area left ungrazed.

Given length of rectangular field = l = 70 m

Breadth of rectangular field = b = 52 m

∴ Area of the field = l × b

⇒ Area of the field = 70 × 52

⇒ Area of the field = 3640 m²

We know in a rectangle all the angles are 90 degrees.

∴ Area available for grazing = area of quadrant

⇒ Area of quadrant/sector = θ/360 × πR²

Where R = radius of circle & θ = central angle

Given R = 21 m and θ = 90°

⇒ Area available for grazing = θ/360 × πR²

Put the given values in the above equation,

⇒ Area available for grazing = 90/360 × π(21²)

(put π = 22/7)

= 90/360 × 22/7 × 441

= (90 × 22 × 441)/(360 × 7)

= (22 × 63)/4

= 1386/4

⇒ Area available for grazing = 346.5 m²

Area left ungrazed = Area of field – Area available for grazing

⇒ Area left ungrazed = 3640 – 346.5

⇒ Area left ungrazed = 3293.5 m²

The area available for grazing is 346.5 m² and area left ungrazed is 3293.5 m².

23. A horse is tethered to one corner of a field which is in the shape of an equilateral triangle of side 12 m. If the length of the rope is 7 m, find the area of the field which the horse cannot graze. Take √3 = 1.732. Write the answer correct to 2 places of decimal.

Solution

Here the horse is tethered to one corner implies or means that the area available for grazing is a sector of radius 21 m with central angle as 60 degrees as the field is in shape of equilateral triangle. Now we need to find the area of this sector to find out the area available for grazing for grazing and then subtract it from the total area of the triangular field to obtain the area left ungrazed.

Given the side of field = a = 12 m

∴ Area of field = Area of equilateral triangle

⇒ Area of field = √3/4 × a²

⇒ Area of field = 1.732/4 × (12²)

⇒ Area of field = (1.732 × 144)/4

⇒ Area of field = 62.352 m²

We know in an equilateral triangle all the angles are 60 degrees.

∴ Area available for grazing = Area of the sector

Area of quadrant/sector = θ/360 × πR²

Where R = radius of circle and θ = central angle of sector

Given r = 7 m and θ = 60°

Put the given values in the above equation,

⇒ Area available for grazing = 60/360 × π(7²) (put π = 22/7)

⇒ Area available for grazing = 60/360 × 22/7 × 49

⇒ Area available for grazing = (60 × 22 × 49)/(360 × 7)

⇒ Area available for grazing = (22 × 7)/6

⇒ Area available for grazing = 154/6 

⇒ Area available for grazing = 25.666 m²

Area that cannot be grazed = Area of field – Area available for grazing

⇒ Area that cannot be grazed = 62.352 – 25.666

⇒ Area that cannot be grazed = 36.686 m²

The area that cannot be grazed is 36.656 m².

25. Four cows are tethered at the four corners of a square of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed? [Take π = 3.14]

Solution

Here, the 4 cows are tethered to each corner implies or means that the area available for grazing is a quadrant of radius 25 m with central angle as 60 degrees as the field is in shape of square. Now, we need to find the area of this sector to find out the area available for grazing for all the cows and then subtract it from the total area of the square field to obtain the area left ungrazed.

The reason why we have taken the radius as 25 m is, basically we have considered that each cow is tethered to a rope which is equal to half of the side of the square as we had to maximize the area each cow gets to graze without sharing thus the maximum radius within which a cow can graze maximum unshared area is simply the half of the side of square.

Given the side of field which is in shape of square = a = 50 m

∴ Area of the field = Area of square

⇒ Area of field = a²

⇒ Area of field = (50²)

⇒ Area of field = 2500 m²

We know in an square all the angles are 90 degrees.

∴ Area available for grazing for one cow = area of sector/quadrant

Area of quadrant/sector = θ/360 × πR²

Where R = radius of circle & θ = central angle of sector

Given R = 25 m & θ = 90°

⇒ Area available for grazing for one cow = θ/360 × πR²

Put the given values in the above equation,

⇒ Area available for grazing for one cow = 90/360 × π(25²) (put π = 3.14)

⇒ Area available for grazing for one cow = 90/360 × 3.14 × 625

⇒ Area available for grazing for one cow = (90 × 3.14 × 625)/360

⇒ Area available for grazing for one cow = (3.14 × 625)/4

⇒ Area available for grazing for one cow = (1962.5)/4

⇒ Area available for grazing for one cow = 490.625 m²

⇒ Area available for 4 cows = 4 × Area available for one cow

⇒ Area available for 4 cows = 4 × 490.625

⇒ Area available for 4 cows = 1962.5 m²

Area left ungrazed = Area of field – Area available for grazing for 4 cows

⇒ Area that cannot be grazed = 2500 – 1962.5

⇒ Area that cannot be grazed = 537.5 m²

The area left ungrazed is 537.5 m².

26. In the given figure, OPQR is a rhombus, three of whose vertices lie on a circle with centre O. If the area of the rhombus is 32√3 cm², find the radius of the circle.

Solution

Here in the given figure ’O’ is the centre on which three vertices of rhombus lie, this implies that OP, OR are both radius of the circle. Also we know that in rhombus all the 4 sides are equal in length. Thus OP, OR, PQ, RQ they all are radii of circle. Also, OQ is equal to radius of circle. Now rhombus being a parallelogram therefore diagonal OQ will divide the rhombus into two equal halves this means that the area of triangle OQR will be equal to half of the area of rhombus. Also we can see that triangle OQR is an equilateral triangle and hence we can easily calculate its area in terms of radius of circle and equate it to half of the area of rhombus and calculate the radius of given circle.

Given area of OPQR = 32√3 cm²

Let the radius of the circle = x cm

Now join OQ

Consider △OQR,

OQ = OR = RQ = x cm

⇒ △OQR is an equilateral triangle

∴ Area of OQR = Area of an equilateral triangle = √3/4 × a² ...(i)

Where a = side of equilateral triangle

Also we know OQ is a diagonal of rhombus OPQR and as in a parallelogram diagonal divides it into two equal area or halves, similarly OQ is also dividing the rhombus into two equal areas therefore,

⇒ Area of △OQR = Area of △OPQ ...(ii)

Area of OPQR = Area of △OQR + Area of △OPQ

Area of OPQR = 2 × Area of △OQR (from eqn2) ...(iii)

Put the values of area of OPQR and equation 1 in equation 3

⇒ 32√3 = 2 × √3/4 × a² (put a = x)

⇒ 32√3 = (2√3)/4 × x²

⇒ 32√3 = √3/2 × x²

⇒ (32√3 × 2)/√3 = x²

⇒ 64 = x²

⇒ x = ±√64

⇒ x = ±8

As every quadratic equation has two roots, similarly x² = 64 also have two roots i.e., x = 8 and x = -8. As we know ‘x’ represents radius of circle therefore it cannot be a negative value, hence we discard the negative root.

Therefore radius of the circle = x = 8 cm

The radius of circle is 8 cm.

27. The side of a square is 10 cm. Find

(i) The area of the inscribed circle, and

(iii) The area of the circumscribed circle. [Take π = 3.14]

Solution

(i) 

Consider the above figure, Join PR,

Now PR = Diameter of the inscribed circle

Also, PR = BC = 10 cm.

So, PR = 10 cm

∴ radius of inscribed circle = r = PR/2

⇒ r = 10/2

⇒ r = 5 cm

∴ Area of inscribed circle = πr² (put value of r in this equation)

⇒ Area of inscribed circle = π(5²)

⇒ Area of inscribed circle = 22/7 × 25 (put π = 22/7)

⇒ Area of inscribed circle = (22 × 25)/7

⇒ Area of inscribed circle = 78.57 cm²

The area of inscribed circle is 78.57 cm².

(ii) 

Consider the above figure, O is the centre and ABCD is a square inscribed. Now OB and OD are radii of circle.

Consider △DBC right angled at c (as C is a vertex of square)

∴ Apply Pythagoras theorem in triangle DBC

Hypotenuse² = Perpendicular² + Base²

In triangle DBC, hypotenuse = DB,

Perpendicular = BC and

Base = DC

⇒ BD² = BC² + DC²

Put the values of BC and DC i.e., 10 cm

⇒ BD² = 10² + 10²

⇒ BD² = 200

⇒ BD = √200

⇒ BD = 10√2 cm

Now radius of circle = half of BD

∴ radius of circle = r = BD/2

⇒ r = (10√2)/2

⇒ r = 5√2 cm

Hence, Area of circumscribing circle = πr²

⇒ Area of circumscribing circle = 3.14 × 5√2 × 5√2

(put π = 3.14 and r = 5√2 cm)

⇒ Area of circumscribing circle = 3.14 × 50

⇒ Area of circumscribing circle = 157 cm²

Area circumscribing circle is 157 cm².

28. If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.

Solution

Consider the figure shown below where O is centre of circle, join BC which passes through O, let the side of square be ‘a’ and radius of circle be ‘r’.

Now we know OB and OC are radius of circle

So, OB = OC = r

Consider △BDC right angled at D

∴ H² = P² + B² (Pythagoras theorem)

⇒ BC² = BD² + DC² ...(i)

And we know BC = OC + OB

BC = 2r and BD = DC = a (put these values in eqn1)

⇒ (2r)² = a² + a²

⇒ 4r² = 2a²

⇒ r² = 2a²/4

⇒ r² = a²/2 ...(ii)

Area of inscribed square = side × side

Area of inscribed square = a × a

Area of inscribed square = a² ...(iii)

Area of circumscribing circle = πR² where R = radius of circle

⇒ Area of circumscribing circle = πr² ...(iv)

Ration of area of circumscribing circle to that of inscribed circle = (area of circle)/(area of square)

Put the values from equation 3 & 4 in above equation

Ratio = πr²/a²

⇒ Ratio = (π × a²/2)/a² (from eqn 2)

⇒ Ratio = (π × a²)/(2 × a²) = π/2

So, ratio is π : 2

29. The area of a circle inscribed in an equilateral triangle is 154 cm². Find the perimeter of the triangle.[Take √3 = 1.73]

Solution

Consider the figure shown above. AF, BE and CD are perpendicular bisector.

Now we know that the point at which all three perpendiculars meet is called incentre, so O is the incentre, thus O divides all three perpendiculars in a ratio 2 : 1.

Let AB = BC = CA = a cm

Therefore let AF = h cm

⇒ ∠AFC = 90° and OF = 1/3 × AF

⇒ OF = h/3 cm (putting value of OF)

⇒ h = 3 × OF ...(i)

And we can see from figure that OF = radius of circle

Now let radius of circle be = r cm

∴ Area of circle = πR²

Where r = radius of circle

Given area of circle = 154 cm²

⇒ πr² = 154

⇒ 22/7 × r² = 154 (put π = 22/7)

⇒ r² = (154 × 7)/22

⇒ r² = 49

⇒ r = 7 cm

Therefore OF = 7 cm

⇒ h = 3 × 7 (from eqn 1)

⇒ h = 21 cm

We know area of an equilateral triangle = √3/4 × a²

Where a = side of triangle

Also, Area of triangle = 1/2 × base × height

Equating both the areas we get,

√3/4 × a² = 1/2 × BC × AF

Put the values of BC and AF

⇒ √3/4 × a² = 1/2 × a × h

√3/4 × a² = 1/2 × a × 21

(putting value of h = 21 cm)

⇒ √3/4 × a = 21/2

⇒ a = (21 × 4)/(2 × √3)

(rationalize it)

⇒ a = (21 × 4 × √3)/(2 × √3 × √3)

⇒ a = (42 × √3)/3

⇒ a = 14√3 cm

∴ Perimeter of equilateral triangle = 3 × side of triangle

⇒ Perimeter of △ABC = 3 × 14√3 (put √3 = 1.73)

⇒ Perimeter of △ABC = 42 × 1.73

⇒ Perimeter of △ABC = 72.66 cm

The perimeter of triangle is 72.66 cm.

30. The radius of the wheel of a vehicle is 42 cm. How many revolutions will it complete in a 19.8 km-long journey ?

Solution

In one revolution a wheel will cover a distance equal to its circumference, so in order to find the number of revolutions we have to first calculate the circumference of the wheel and then divide it with the total distance covered to find out the total number of revolutions

Given radius of wheel = r = 42 cm

Circumference of wheel = 2πR where R = radius of the wheel

= 2π(42) (putting value of r)

Circumference of wheel = (2 × 22 × 42)/7 = 264 cm

Therefore distance covered in one revolution = 264 cm

Total distance covered = 19.8 km = 1980000 cm

Total number of revolutions = n

Distance covered on 1 revolution × no. of revolutions = Total distance

264 × n = 1980000

⇒ n = 1980000/264

⇒ n = 7500

Total number of revolutions is 7500.

31. The wheels of the locomotive of a train are 2.1 m in radius. They make 75 revolutions in one minute. Find the speed of the train in km per hour.

Solution

Given radius of wheel = R = 2.1 m

Number of revolutions in one minute = 75

Number of revolutions in 1 hour = 75 × 60

Number of revolutions in 1 hour = 45000

Distance covered in one revolution = Circumference of wheel

Distance covered in one revolution = 2πR (where R = radius of wheel)

Distance covered n 1 revolution = 2π(2.1)

Distance covered in one revolution = 2 × 22/7 × 2.1 (put π = 22/7)

= 13.2 m

So, distance covered in 4500 revolutions = 4500 × distance covered in 1

Distance covered in 4500 revolution = 4500 × 13.2

Distance covered in 4500 revolutions = 59400 m = 59.4 km

∴ Distance covered in 1 hour = 59.4 km

Hence speed of the locomotive = 59.4 km/hr

The speed of locomotive is 59.4 km/hr

32. The wheels of a car make 2500 revolutions in covering a distance of 4.95 km. Find the diameter of a wheel.

Solution

Let the diameter f the wheel be ‘d’ cm

Total distance covered in 250 revolutions = 49.5 km = 495000 m

Distance covered in one revolution = 495000/2500

⇒ Distance covered in one revolution = 198 cm ...(i)

Also, Distance covered in one revolution = circumference of wheel

∴ Distance covered in one revolution = πD where d = diameter of wheel

Distance covered in one revolution = (22 × d)/7 ...(ii) (put π = 22/7)

Equate equation 1 and 2 we get,

(22 × d)/7 = 198

⇒ d = (198 × 7)/22

⇒ d = 9 × 7

⇒ d = 63 cm

The diameter of the wheel is 63 cm.

33. A boy is cycling in such a way that the wheels of his bicycle are making 140 revolutions per minute. If the diameter of a wheel is 60 cm, calculate the speed (in km/h) at which the boy is cycling.

Solution

Given number of wheel = d = 60 cm

Number of revolutions in one minute = 140

Number of revolutions in one hour = 140 × 60

Number of revolutions in one hour = 8400

Distance covered in one revolution = circumference of wheel

⇒ Distance covered in one revolution = πd

Distance covered in one revolution = 22/7 × 60 (put π = 22/7 and value of d)

= 188.57 cm

Distance covered in one hour = Distance in 1 revolution × no. of revolutions

⇒ Total distance covered in one hour = 188.57 × 8400

⇒ Total distance covered in one hour = 1583988 cm = 15.839 km

∴ Speed with which boy is cycling = 15.839 km/hr

The speed with which boy is cycling is 15.839 km/hr.

34. The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour ?

Solution

Given diameter of wheel of bus = d = 140 cm

So radius of wheel = R = d/2 = 140/2 = 70 cm

Speed of bus = 72.6 km/hr

∴ Distance covered by bus in one hour = 72.6 km = 7260000 cm

So distance covered by wheels in one minute = 7260000/60

Distance covered in one minute = 121000 cm ...(i)

Let the number of revolutions made by wheel per minute = x

Distance covered by wheel in one revolution = circumference of wheel = 2πR

Distance covered by wheel in one revolution = 2π(70) (putting value of R)

= 2 × 22/7 × 70 (putting value or R and π = 22/7)

= (2 × 22 × 70)/7

= 2 × 22 × 10

= 440 cm

∴ Total distance = No. of revolution × Distance covered in 1 revolution

On putting the required values we get,

121000 = 440 × (x)

⇒ x = 121000/440

⇒ x = 275

Number of revolutions made per minute is 275.

35. The diameters of the front and rear wheels of a tractor are 80 cm and 2 m respectively. Find the number of revolutions that a rear wheel makes to cover the distance which the front wheel covers in 800 revolutions.

Solution

Given diameter of front wheel = d = 80 cm

So, radius of front wheel = r = d/2 = 80/2 = 40 cm

Diameter of rear wheel = D = 2 m = 200 cm

So, Radius of front wheel = R = D/2 = 200/2 = 100 cm.

Distance covered by wheel in 1 revolution = Circumference of wheel

⇒ Distance covered by front wheel = 2πr = 2π(40)

⇒ Distance covered by front wheel = 80π

∴ Distance covered by front wheel in 800 revolutions = 80π × 800

⇒ Distance covered by front wheel in 800 revolutions = 6400π - eqn1 

Similarly

⇒ Distance covered by rear wheel = 2πR = 2π(100)

⇒ Distance covered by rear wheel = 200π -eqn2

Let the number of revolutions made by rear wheel to cover 6400π cm be “x”

∴ (x) × 200π = 6400π (from eqn1 and eqn2)

⇒ x = 64000π/200π

⇒ x = 64000/200

⇒ x = 320

Number of revolution made by rear wheel to cover the distance covered by front wheel in 800 revolutions is 320.

36. Four equal circles are described about the four corners of a square so that each touches two of the others, as shown in the figure. Find the area of the shaded region, if each side of the square measures 14 cm.

Solution

Here the distance between the center of circles touching each other is equal to the side of the square. Therefore, we can say that the radius of each circle is equal to the half of the side of the square. Now by simply calculating the area of the 4 quadrants and then subtracting it from the area of the square we can easily calculate the area of the shaded region.

Given side of square = a = 14 cm

Central angle of each sector formed at corner = θ = 90°

So, radius of 4 equal circles = r = a/2 = 14/2

∴ Radius of 4 circles = r = 7 cm

Area of quadrant formed at each corner = θ/360 × πR²

Where R = radius of circle

⇒ Area of one quadrant = 90/360 × π(7²)

= 49π/4 cm² ...(i)

Area of all the 4 quadrant = 4 × Area of one quadrant

= 4 × 49π/4 (from eqn 1)

⇒ Area of all 4 quadrants = 49π ...(ii)

Also, Area of square = side × side = a × a = a² = 14² (putting value of side of square)

⇒ Area of square = 196 cm² - eqn3

∴ Area of shaded region = Area of square – Area of all 4 quadrants

⇒ Area of shade region = 196 - 49π (from eqn3 and eqn 2)

 ⇒ Area of shaded region = 196 – (49 × 22/7) (put π = 22/7)

= 196 – (7 × 22)

= 196 – 154

= 42 cm²

The area of shaded region is 42 cm².

37. Four equal circles, each of radius 5 cm, touch each other, as show in the figure. Find the area included between them. [Take π = 3.14]

Solution

Here, first we join the center of all adjacent circles then the distance between the center of circles touching each other is equal to the side of the square formed by joining the center of adjacent circles. Therefore, we can say that the side of the square equal to the twice of the radius of circle. Now by simply calculating the area of the 4 quadrants and then subtracting it from the area of the square we can easily calculate the area of the shaded region.

Given radius of each circle = r = 5 cm

Central angle of each sector formed at corner = θ = 90°

Side of square ABCD = a = 2 × r = 2 × 5 = 10 cm

Area of quadrant formed at each corner = θ/360 × πR²

Where R = radius of circle

⇒ Area of one quadrant = 90/360 × π(5²)

(putting value of r and θ)

 = 25π/4 cm² ...(i)

Area of all 4 quadrants = 4 × Area of one quadrant

= 4 × 25π/4 (from eqn 1)

⇒ Area of all 4 quadrants = 25π ...(ii)

Area of square = side × side = a × a = a²

⇒ Area of square = 10² (putting value of side of square)

⇒ Area of square = 100 cm² ...(iii)

Area of shaded region = Area of square – Area of all 4 quadrants

Area of shaded region = 100 - 25π (from eqn3 and eqn2)

= 100 – (25 × 3.14) (put π = 3.14)

= 100 – 78/.5

= 21.5 cm²

The area of shaded region is 21.5 cm².

38. Four equal circles, each of radius a units, touch each other. Show that the area between them is (6/7.a²) sq. units.

Solution

Here, first we join the centre of all adjacent circles then the distance between the centre of circles touching each other is equal to the side of the square formed by joining the centre of adjacent circles. Therefore, we can say that the side of the square equal to the twice of the radius of circle. Now by simply calculating the area of the 4 quadrants and then subtracting it from the area of the square we can easily calculate the area of the shaded region.

Given radius of each circle = “a” units

Central angle of each sector formed at corner = θ = 90°

Side of square ABCD = 2 × a units

Area of quadrant formed at each other = θ/360 × πR²

Where R = radius of circle

⇒ Area of one quadrant = 90/360 × π(a²)

⇒ Area of one quadrant = πa²/4 sq. units ...(i)

∴ Area of all 4 quadrants = 4 × Area of one quadrant

⇒ Area of all the 4 quadrant = 4 × πa²/4 (from eqn 1)

 = πa² sq. units ...(ii)

Area of square = side × side = 2a × 2a = 4a²

⇒ Area of square = 4a² sq. units -eqn3

Area of shaded region = Area of square – Area of all 4 quadrants

⇒ Area of shaded region = 4a² – πa² (from eqn3 and eqn2)

⇒ Area of shaded region = 4a² – (a² × 22/7) (put π = 22/7)

⇒ Area of the shaded region = 4a² – 22a²/7

⇒ Area of shaded region = (28a² – 22a²)/7

⇒ Area of shaded region = 6a²/7 sq. units

Area of shaded region is 6a²/7 sq. units

39. Three equal circles, each of radius 6 cm, touch one another as shown in the figure. Find the area enclosed between them. [Take π = 3.14 and √3 = 1.732]

Solution

Consider the above figure,

Here, first we join the centre of all adjacent circles then the distance between the center of circles touching each other is equal to the side of an equilateral triangle formed by joining the center of adjacent circles. Therefore, we can say that the side of the equilateral triangle is equal to the twice of the radius of circle. Now by simply calculating the area of the 3 sectors and then subtracting it from the area of the equilateral triangle we can easily calculate the area of the enclosed region.

Given radius of each circle = r = 6 cm

Central angle of each sector = θ = 60° (∵△ABC is equilateral)

Side of equilateral △ABC = a = 2 × r = 2 × 6

∴ Side of equilateral △ABC = a = 12 cm

Area of sector formed at each other = θ/360 × πR² where R = radius of circle

⇒ Area of one sector = 60/360 × π(6²)

⇒ Area of one sector = 36 π/6 cm²

⇒ Area of one sector = 6π cm² ...(i)

Area of all the 3 sector = 3 × Area of one sector

= 3 × 6π (from eqn1)

= 18π cm² ...(ii)

Area of equilateral △ABC = √3/4 × a² = √3/4 × (12²)

⇒ Area of equilateral △ABC = (√3 × 144)/4

⇒ Area of equilateral △ABC = 36△3 cm² ...(iii)

Area of enclosed region = Area of equilateral △ABC – Area of all 3 sectors

⇒ Area of enclosed region = 36√3 - 18π (from eqn 3 and eqn 2)

⇒ Area of enclosed region = (36 × 1.732) – (18 × 3.14)

(put π = 3.14 & √3 = 1.732)

= 62.352 – 56.52

= 5.832 cm²

The area of enclosed region is 5.832 cm².

40. If three circles of radius a each, are drawn such that each touches the 4 other two, prove that the area included between them is equal to 4/25.a² [Take = √3 = 1.73 and π = 3.14]

Solution

Consider the figure shown below

Here, first we join the center of all adjacent circles then the distance between the center of circles touching each other is equal to the side of an equilateral triangle formed by joining the center of adjacent circles. Therefore, we can say that the side of the equilateral triangle is equal to the twice of the radius of circle. Now by simply calculating the area of the 3 sectors and then subtracting it from the area of the equilateral triangle we can easily calculate the area of the enclosed region.

Given radius of each circle = “a” units

Central angle of each sector = θ = 60° (∵△ABC is equilateral)

Side of equilateral △ABC = 2 × a units

Area of sector formed at each corner = θ/360 × πR²

⇒ Area of one sector = 60/360 × π(a²)

⇒ Area of one sector = πa²/6 sq. units ...(i)

∴ Area of all 3 sectors = 3 × Area of one sector

⇒ Area of all 3 sector = 3 × (πa²)/6 (from eqn1)

= (πa²)/2 sq. units ...(ii)

Area of equilateral △ABC = √3/4 × (2a)²

= (√3 × 4a²)/4

= a²√3 sq. units ...(iii)

Area of enclosed region = Area of equilateral △ABC – Area of all 3 sectors

⇒ Area of enclosed region 

= a²√3 – πa²/2 (from eqn 3 and eqn 2)

= a² ×1.73 – (3.14 × a²)/2

= (a² ×1.73×2 – 3.14×a²)/2

= (3.46 – 3.14)a²/2 (taking a² common)

⇒ Area of the enclosed region = 0.32a²/2

= 32a²/200

= 4a²/25 sq. units

Area of the enclosed region is 4a²/25 sq. units

41. In the given figure, ABCD is a trapezium of area 24.5 cm². If AD || BC, ∠DAB = 90°, AD = 10 cm, AD = 10 cm, BC = 4 cm, and ABE is quadrant of a circle then find the area of the shaded region.

Solution

Here in order to find the area of the shaded region we have to calculate the area, or the quadrant shown and subtract it from the area of the trapezium. And in order to find the area of the quadrant we have to calculate the radius of the sector EAB by the area of trapezium.

Given Area of trapezium ABCD = 24.5 cm² ...(i)

AD || BC, AD = 10 cm, BC = 4 cm, ∠DAB = 90°

We also now Area of trapezium = 1/2 × (sum of parallel sides) × height

Area of trapezium = 1/2 × (AD + BC) × AB ...(ii)

Putting the values in equation 2, we get,

24.5 = 1/2 × (10 + 4) × AB

⇒ 24.5 = (14 × AB)/2

⇒ 24.5 = 7AB

⇒ AB = (24.5)/7

⇒ AB = 3.5 cm

Therefore radius of the sector EAB = r = 3.5 cm

Area of quadrant EAB = θ/360 × πR² where R = radius of the sector

⇒ Area of quadrant EAB = 90/360 × π(3.5²) (put π = 22/7)

⇒ Area of the quadrant = 90/360 × 22/7 × 3.5 × 3.5

⇒ Area of the quadrant EAB = (22 × 3.5 × 3.5)/(4 × 7)

⇒ Area of the quadrant EAB = 269.5/28

⇒ Area of the quadrant EAB = 9.625 cm² -eqn3

∴ Area of shaded region = Area of trapezium – Area of quadrant EAB

⇒ Area of shaded region = 24.5 – 9.625 (putting values from eqn1 and eqn3)

⇒ Area of shaded region = 14.875 cm²

42. ABCD is a field in the shape of a trapezium, AD ||BC, ∠ABC = 90° and ∠ADC = 90°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m.

Find the following:

(i) total area of the four sectors,

(ii) area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

Solution

Here in order to find the area of the shaded region we have to calculate the area, or the quadrant shown and subtract it from the area of the trapezium. And in order to find the area of the quadrant we have to calculate the radius of the sector EAB by the area of trapezium.

Given AB = 30 m, AD = 55m, BC = 45 m

θ_A = 90°, θ_B = 90° θ_C = 120°, θ_D = 60°

Radius of each sector = r = 14 m

(i) total area of 4 sectors

Area of sector = θ_i/360 × πR² ...(i)

= θA/360 × πR²

Area of sector at corner A = 90/360 × π × 14² (putting values in eqn 1)

Area of sector at corner A = 196π/4

Area of sector at corner A = 49π m² ...(ii)

As we know that central angle at A and B are both 90 degrees and radius is also same i.e., 14 m therefore the area of the sector at B will be exactly same as that of sector at A.

∴ Area of sector at corner B = Area of sector at corner A

⇒ Area of sector at corner B = 49π ...(iii)

Similarly,

Area of sector = C/360 × πR² 

Area of sector at corner C = 120/360 × π × 14² (putting values in eqn 1)

Area of sector at corner C = (196π)/3

Area of sector at corner C = 65.33π m² ...(iv)

Similarly,

Area of sector = θD/360 × πR²

Area of sector at corner D = 60/360 × π × 14² (putting values in eqn 1)

Area of sector at corner D = 196π/6

Area of sector at corner D = 32.67π ...(v)

Total area of 4 sectors = eqn2 + eqn3 + eqn4 + eqn5

⇒ Total area = 49π + 49π + 65.33π + 32.67π

⇒ Total area of 4 sectors = 196π

Total area of 4 sectors = 196π

Total area of 4 sectors = 196 × 22/7 (put π = 22/7)

∴ Total area of 4 sectors = 616 m²

Total area of 4 sectors is 616 m².

(ii) Area of the remaining portion.

Here in order to find the area of the remaining portion of the trapezium we have to subtract the area of the 4 sectors from the area of the trapezium.

Area of trapezium = 1/2 × (sum of parallel sides) × height

Area of trapezium = 1/2 × (AD + BC) × AB

On putting the values,

Area of trapezium = 1/2 × (55 + 45) × 30

= (100 × 30)/2

= 50 × 30

Area of trapezium = 1500 m² ...(i)

Area of remaining portion = Area of trapezium – Area of the 4 sectors

⇒ Area of remaining potion = 1500 – 616 (from eqn 1 and part (i))

∴ Area of remaining portion = 884 m²

The area of the remaining portion is 884 m².

43. Find the area of the shaded region in the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle of side 12 cm as centre and a sector of circle of radius 6 cm with centre B is made. [Use √3 = 1.73 and π = 3.14]

 Solution

Area of shaded region can be calculated by subtracting the area of minor sector at O and area of equilateral triangle.

Given Radius of circle at O = r = 6 cm

Side of equilateral triangle = a = 12 cm

Central angle at O = 360 – 60 = 300°

Central angle at B = 60°

Area of the equilateral triangle = √3/4 × a²

Where a = side of equilateral triangle

Area of the equilateral triangle = √3/4 × (12)² (putting the value of a)

Area of the equilateral triangle = (144 × √3)/4

Area of the equilateral triangle = 36√3 cm² ...(i)

Area of sector = θ/360 × πR² where r = radius of the sector

Area of minor sector at B = 60/360 × π × (6²) (given)

∴ Area of minor sector at B = 6π cm² ...(ii)

Similarly,

Area of major at O = 300/360 × π(6²)

∴ Area of major sector at O = 30π cm² ...(iii)

Area of shaded region = eqn1 + eqn3 – eqn 2

On putting values

⇒ Area of shaded region = 36√3 + 30π - 6π

Area of shaded region = 36√3 + 24π

(put π = 3.14 and √3 = 1.73)

∴ Area of shaded region = (36 × 1.73) + (24 × 3.14)

⇒ Area of shaded region = 62.28 + 75.36

∴ Area of shaded region = 137.64 cm²

Area of the shaded region is 137.64 cm².

44. In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.

Solution

Here in order to find the area of the shaded region we have to subtract the area of the semicircle and the triangle from the area of the rectangle.

Given AB = 80 cm, BC = 70 cm, DE = 42 cm, ∠AED = 90°

Here we see that the triangle AED is right angle triangle, therefore, we can apply Pythagoras theorem i.e.,

H² = P² + B² (Pythagoras theorem)

AD² = DE² + AE² 

⇒ 70² = 42² + AE² (putting the given values)

⇒ 4900 = 1764 + AE²

⇒ 4900 – 1764 = AE²

⇒ 3136 = AE²

AE = √3136

∴ AE = 56 cm

Area of △ = 1/2 × AE × DE

(Area of triangle = 1/2 × base × height)

On putting values we get,

Area of △AED = 1/2 × 56 × 42

⇒ Area of △AED = 28 × 42

∴ Area of △AED = 1176 cm² ...(i)

Area of semicircle = πR²/2

Here radius of semicircle = BC/2 = 70/2

R = 35 cm

∴ Area of semicircle = (π × 35²)/2

Area of semicircle = (22 × 1225)/(2× 7) (putting π = 22/7)

⇒ Area of semicircle = 11× 175

∴ Area of semicircle = 1925 cm² ...(ii)

Area of rectangle = l × b (l = length of rectangle, b = breadth of rectangle)

⇒ Area of rectangle = 80 × 70 = 5600 cm² ...(iii)

Area of shaded region = Area of rectangle – Area of semicircle – Area of △

⇒ Area of shaded region = 5600 - 1925 – 1176 (from eqn1, eqn2 and eqn3)

∴ Area of shaded region = 2499 cm²

Area of the shaded region is 2499 cm².

45. In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region. [Use π = 3.14]

Solution

Here in order to find the area of the shaded region (region excluding the triangle) we have to subtract the area of the triangle from the area of the rectangle and then add the area of the semicircle.

Given AB = 20 cm, DE = 12 cm, AE = 9 cm and ∠AED = 90°

Here we see that the triangle AED is right angle triangle, therefore, we can apply Pythagoras theorem i.e.,

H² = P³ + B² (Pythgoras theorem)

AD² = DE² + AE²

AD² = 12² + 9² (putting given values)

⇒ AD² = 144 + 81

⇒ AD² = 225

⇒ AD = √225

∴ AD = 15 cm

Area of △AED = 1/2 × AE × DE

(Area of triangle = 1/2 × base × height)

On putting values we get,

Area of △AED = 1/2 × 9 × 12

⇒ Area of △AED = 9 × 6

∴ Area of △AED = 54 cm² ...(i)

Area of semicircle = πR²/2

Here radius of semicircle = BC/2 = 15/2

⇒ R = 7.5 cm

∴ Area of semicircle = (π × 7.5²)/2

Area of semicircle = (3.14 × 56.25) (putting π = 3.14)

⇒ Area of semicircle = 1.07 × 56.25

∴ Area of semicircle = 88.3125 cm² ...(ii)

Area of rectangle = l × b (l = length of rectangle, b = breadth of rectangle)

⇒ Area of rectangle = 20 × 15 (putting the values of l & b)

∴ Area of rectangle = 300 cm² ...(iii)

Area of shaded region = Area of rectangle + Area of semicircle – Area of △

⇒ Area of shaded region = 300 + 88.3125 – 53 (from eqn1, eqn2, eqn3)

∴ Area of shaded region = 334.3125 cm²

Area of shaded region is 334.3125 cm².

46. In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region. [Use π = 3.14].

Solution

Here in order to find the area of the shaded region (region excluding the area of segment AC and Quadrant OCD) can be calculated by subtracting the area of triangle and quadrant OBD from the area of the circle.

Given AC = 24 cm, AB = 7 cm and ∠BOD = 90°.

Here we see that the triangle ACB is right angle triangle, therefore, we can apply Pythagoras theorem i.e.,

H² = P² + B² (Pythagoras theorem)

BC² = AC² + AB²

⇒ BC² = 24² + 7² (putting the given values)

⇒ BC² = 576 + 49

⇒ BC² = 625

BC = √625

∴ BC = 25 cm

Area of △ACB = 1/2 × AB × AC (Area of triangle = 1/2 × base × height)

On putting values we get,

Area of △ACB = 1/2 × 7 × 24

⇒ Area of △AED = 7 × 12

∴ Area of △AED = 84 cm² ...(i)

Area of circle = πR² (R = radius of circle)

Here radius of circle = BC/2 = 25/2 (because ABCD is a rectangle)

⇒ R = 12.5 cm

 ∴ Area of circle = π × 12.5²

⇒ Area of circle = 156.25 × 3.14 (put π = 3.14)

∴ Are of circle = 490.625 cm² ...(ii)

Area of quadrant OBD = θ/360 × πR²

Area of quadrant OBD = 90/360 × π × 12.5² (put π = 3.14)

Area of quadrant = (3.14 × 156.25)/4

⇒ Area of quadrant OBD = 122.65625 cm² ...(iii)

Area of shaded region = Area of circle – Area of quadrant – Area of △

⇒ Area of shaded region = 490.625 – 84 – 122.65625 (from eqn1, 2 and 3)

⇒ Area of shaded region = 283.96875 cm²

Area of shaded region is 283.96875 cm².

47. In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3 = 1.73 and π = 3.14.]

Solution

Here we will draw median from all the vertices of the equilateral triangle and the point at which they intersect will be the centre of the circle. Then with the help of which find out the height of the triangle and subsequently the radius of the circle and ultimately the area of the shaded region (region of equilateral triangle excluding the area of circle inscribed.)

As AD = BF = CE = h

Consider △ADB, ∠ADB = 90°, BD = 6 cm

AB² = AD² + BD² (Pythagoras theorem)

12² = AD² + 6² (putting the given values)

144 = AD² + 36

144 – 36 = AD²

We also know that a point O will divide each median in a ratio of 2 : 1.

So, OD = h/3

OD = (6√3)/3

OD = 2√3 cm

∴ Radius of the circle = r = 2√3 cm

Area of the circle = πr²

Area of the circle = π × (2√3)² (putting the value of r)

∴ Area of the circle = 12π cm² ...(i)

Area of △ABC = √3/4 × a² where a = side of equilateral triangle

Area of △ABC = √3/4 × 12²

Area of △ABC = (144 × √3)/4

Area of △ABC = 36√3 cm² ...(ii)

Area of shaded region = area of triangle – area of circle

Area of the shaded region = 36√3 - 12π (put π = 3.14 & √3 = 1.73)

⇒ Area of the shaded region = (36 × 1.73) – (12 × 3.14)

⇒ Area of the shaded region = 62.28 – 37.68

∴ Area of the shaded region = 24.6 cm²

The radius of the circle is 2√3 cm and area of shaded region is 24.6 cm²

48. On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. [Use √ = 1.73].

Solution

Here we will first find the sides of equilateral triangle ant then subtract the area of the triangle from the area of the circle.

Given radius of circle = r = 42 cm

∴ Area of the circle = πR², where R = radius of the circle

⇒ Area of the circle = π(42²)

∴ Area of circle = 22/7 × 1764 (putting π = 22/7)

⇒ Area of the circle = 22 × 252

∴ Area of the circle = 5544 cm² ...(i)

Consider the figure shown,

In △ABD, ∠ADB = 90°

∴ AB² = AD² + BD² ...(ii) (Pythagoras theorem)

Let the sides of the equilateral triangle = a cm

And as we know AD is a median therefore it will bisect the side BC into two equal parts i.e.,

BD = DC ...(iii)

Also, BC = BD + DC

⇒ BC = BD + BD (from eqn3)

⇒ a = 2BD (BC = a)

BD = a/2 cm

So, a² = AD² + (a/2)² (putting values of AC and BD in eqn2)

⇒ a² = AD² + a²/4

⇒ a² – a²/4 = AD²

⇒ (4a² – a²)/4 = AD²

= 3a²/4 = AD²

Now, we also know that the point ‘O’ which is the intersection of all the three medians i.e., centroid of the triangle. Also we know that the centroid divides the median in the ratio 2: 1,

So, we can say that AO = 2AD/3

Also, we know AO = radius = r = 42 cm

∴ 42 = 2AD/3

⇒ (42 × 3)/2 = AD

⇒ AD = 63 cm

Putting the value in equation 4,

63 = (a√3)/2

⇒ (63 × 2)/ √3 = a

⇒ 126/√3 = a

⇒ 126 × √3)/( √3 × √3) = a (rationalizing L.H.S.)

⇒ 126√3)/3 = a

⇒ a = 42√3 cm

O, area of equilateral triangle ABC = √3/4 × a² (where a = side of triangle)

⇒ Area of triangle ABC = √3/4 × (42√3)² (putting the value of a)

⇒ Area of triangle ABC = √3/4 × (1764 × 3)

⇒ Area of triangle ABC = √3/4 × 5292

⇒ Area of triangle ABC = 1323√2 cm² ...(v)

Area of covered by design = Area of circle – Area of triangle ABC

Area covered by design = 5544 - 1323√3 (from eqn1 and eqn5)

⇒ Area covered by design = 5544 – (1323 × 1.73) (putting √3 = 1.73)

⇒ Area covered by design = 5544 – 2288.79

∴ Area covered by design = 3255.21 cm²

Area covered by design is 3255.21 cm².

49. The perimeter of the quadrant of a circle is 25 cm. Find its area.

Solution

We know perimeter of a sector = Length of its arc + 2R ...(i)

Where R = Radius of the sector.

Perimeter = 25 cm

Also, length of arc of sector = θ/360 × 2πR

θ = 90°

∴ 25 = 90/360 × 2πR + 2R (putting the values in eqn1)

⇒ 25 = 2πR/4 + 2R

⇒ 25 = πR/2 + 2R

⇒ 25 (πR + 4R)/2 (taking 2 as L.C.M on R.H.S)

⇒ 25 × 2 = (π + 4)R (taking R common)

⇒ 50 = (22/7 + 4)R (putting π = 22/7)

⇒ 50 = {(22 + 28)/7}R (taking 7 as L.C.M. on R.H.S)

⇒ 50 × 7 = 50R

⇒ (50 × 7)/50 = R

⇒ R = 7 cm ...(ii)

Area of a sector = θ/360 × πR²

⇒ Area of quadrant = 90/360 × π(7²) (putting the value θ and R)

⇒ Area of quadrant = 49π/4 (put π = 22/7)

⇒ Area of quadrant = (49 × 22)/(4 × 7)

⇒ Area of the quadrant = (7 × 11)/2

∴ Area of the quadrant = 38.5 cm²

Area of the quadrant is 38.5 cm².

50. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]

Solution

Given the radius of the circle = 42 cm

Central angle of the sector = θ = 90°

Area of the minor segment = Area of sector – area of the right angle triangle

Area of the sector = θ/360 × πR²

Area of the sector = 90/360 × π(10²) (putting the values of θ and R)

⇒ Area of the sector = 100π/4 (put π = 3.14)

⇒ Area of the sector = (100 × 3.14)/4

⇒ Area of sector = 25 × 3.14

∴ Area of the sector = 78.5 cm² ...(i)

Area of triangle = 1/2 × base × height

⇒ Area of triangle = 1/2 × 10 × 10

∴ Area of triangle = 50 cm² ...(ii)

Area of the minor segment = 78.5 – 50 (from eqn1, eqn2)

∴ Area of the minor segment = 28.5 cm²

51. The radius of a circular region is 100 m. There is a road 10 m wide, running all around it. Find the area of the road and the cost of levelling it at Rs 20 per m². [Use π = 3.14]

Solution

Here we will first out the area of the road running around the circular garden and then multiplying it with rate per square meter to calculate the cost of leveling.

Here we see in the figure there are two concentric circles so,

Area of road = Area of outer circle – Area of circular garden

Area of circle = πR² (where R = radius of circle) ...(i)

Let the radius of inner circle = r = 100 m

Also, radius of outer circle = R = 110 m (R = r + 10)

Area of outer circle = π(110)² ...(ii) (putting R in eqn1)

Area of inner circle = π(100)² ...(iii) (putting r in eqn1)

∴ Area of road = π(110)² – π(100)² (from eqn2 and 3)

 ⇒ Area of road = π(12100 – 10000)

⇒ Area of road = 2100π (put π = 3.14)

⇒ Area of road = 2100 × 3.14

∴ Area of road = 6594 m²

Cost of levelling = Rate of levelling × Area of road

⇒ Cost of travelling = 20 × 6594

∴ Cost of levelling = Rs 131880

Area of road is 6594 m² and cost of levelling is Rs. 131880.

52. The area of an equilateral triangle is 49√3 cm². Taking each angular point as centre, circles are drawn with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. [Take √3 = 1.73]

Solution

Area of equilateral triangle = 49√3 cm²

Each angle of triangle = θ = 60°

Area of triangle not included in circles = Area of triangle – Area of all sectors

Area of all 3 sectors area equal as all the three circles are having same radius which is equal to the half of the side of the equilateral triangle.

Let the side of equilateral triangle be = a cm

Also, area of equilateral triangle = √3/4 × a² (a = side of triangle)

49√3 = √3/4 × a² (equating the value of area to the above equation)

⇒ (49√3 × 4)/√3 = a²

⇒ a² = 49 × 4

⇒ a = 7 × 2

⇒ a = 14 cm

So, radius of the circles = 7 cm

Area of sector = θ/360 × πr²

Area of sector = 60/360 × π(7)²

Area of sector = (22 × 49)/(6 × 7) (put π = 22/7)

Area of sector = (11 × 7)/3

Area of sector = 77/3 cm²

Area of 3 sector = 3 × area of one sector

Area of 3 sector = 3 × 77/3

∴ Area of all 3 sectors = 77 cm² ...(i)

Area of triangle not included in circles = 49√3 – 77 (putting value of area of triangle and sector)

Area of triangle not included = (49 × 1.73) – 77

⇒ Area of triangle not included = 84.77 – 77

∴ Area of triangle not included = 7.77 cm²

Area of triangle not included in circles is 7.77 cm².

53. A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⟂ CD, HQ ⟂ FI and EL ⟂ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure. [Take π = 3.14]

Solution

Area of whole figure = ar ||ABCD + ar||FGHI + ar DCIF + ar△DEF + Area of semicircle

CD = 8 cm, BP = HQ = 4 cm, DF = EF = 5 cm, CI = 8 cm

ar|| ABCD = ar||FGHI = base × height

⇒ ar|| ABCD = ar||FGHI = BP × DC

⇒ ar||ABCD = ar||FGHI = 4 × 8

⇒ ar||ABCD = ar||FGHI = 32 cm² ...(i) & (ii)

ar DCIF = area of square = side × side

⇒ ar DCIF = DC × CI

⇒ ar DCIF = 8 × 8

⇒ ar DCIF = 64 cm² ...(iii)

Consider △DEF, EF ⟂ DF and △DEF is isosceles

So, FL = LD

FL = LD = 8/2

⇒ FL = LD = 4 cm

In △DEL, ∠DLE = 90°

ED² = EL² + LD² (Pythagoras theorem)

⇒ 5² = EL² + 4² (putting the values)

⇒ 25 = EL² + 16

⇒ 25 – 16 = EL²

⇒ EL² = 9

⇒ EL = √9

∴ EL = 3 cm

Area of △DEF = 1/2 × base × height

⇒ Area of △DEF = 1/2 × DF × EL

⇒ Area of △DEF = 1/2 × 8 × 3

⇒ Area of △DEF = 4 × 3

∴ Area of △DEF = 12 cm² ...(iv)

Area of semicircle = πR²/2 where R = radius of the semicircle

R = 4 cm

Area of semicircle = π(4)²/2 (put π = 3.14)

Area of semicircle = (3.14 × 16)/2

⇒ Area of semicircle = 3.14 × 8

∴ Area of semicircle = 25.12 cm² ...(v)

Area of whole figure = (i) + (ii) + (iii) + (iv) + (v)

⇒ Area of whole figure = 32 + 32 + 64 + 12 + 25.12

∴ Area of whole figure = 165.12 cm²

Area of the whole figure is 165.12 cm².

54. A circular disc of radius 6 cm is divided into three sectors with central angle 90°, 120° and 150°. What part of the whole circle is the sector with central angle 150°? Also, calculate the ratio of the areas of the three sectors.

Solution

θ₁ = 90°, θ₂ = 120°, θ₃ = 150°

Radius of circle = r = 6 cm

Area of sector = θ/360 × πR² ...(i)

Area of circle = πR²

⇒ Area of circle = π × 6²

⇒ Area of circle = 36π ...(ii)

Area of sector (θ₃) = 150/360.π × 6² (from i)

Area of sector (θ₃) = 15π/36 × 36

Area of sector (θ₃) = 15/36 × 36π

Area of sector (θ₃) = 15/36 × Area of circle (from ii)

Area of sector (θ₃) = 5/12 × Area of circle

Area of sector (θ₃) = 15π cm²

Area of sector (θ₂) = 120/360 × π6² (putting values in i)

Area of sector (θ₂) = 12/36 × 36 π

Area of sector (θ₂) = 12π cm²  ...(iii)

Area of sector (θ₁) = 90/360 × π6² (putting values in i)

Area of sector (θ₁) = 9/36 × 36π

Area of sector (θ₁) = 9π cm² ...(iv)

Ratio of three sectors = 9π : 12π : 15π

Ratio of three sectors : : 3 : 4 : 5

Area of sector (θ₃) is 5/12 × Area of circle and Ratio of three sectors : : 3 : 4: 5. 

55. A round table covers has six equal designs as shown in the given figure. If the radius of the cover is 35 cm then find the total area of the design. [Use = √3 = 1.732 and π = 3.14.]

Solution

Total area of design = Area of all the minor segments

Here we will find out the area of one segment and then multiply it with 6 to get the total area of design. And as the figure inscribed in the circle is a regular hexagon this implies that it will be having all edges of same length. Therefore we can say that the angle subtended by each chord which are actually the edges of regular hexagon are equal (theorem).

Let angle subtended by chord AB on centre O be θ

So angle subtended = θ = 360/6

∴ Angle subtended = θ = 60°

Radius of circle = 35 cm

Area of sector = θ/360 × πR² ...(i)

Area of one sector = 60/360 × π(35)² (putting values in i)

Area of one sector = 1225π/6 cm²

Area of △OAB = 1/2 × 35 × 35 × sin θ (where θ = central angle of sector)

Area of △OAB = 1/2 × OA × OB × sin 60

Area of △OAB = 1/2 × 1225 × √3/2 (sin 60 = √3/2)

Area of △OAB = (1225√3)/4 cm²

Area of minor segment OAB = Area of sector – Area of △OAB

Area of minor segment OAB = (1225π)/6 – (1225√3)/4 (put π = 3.14 & √3 = 1.732)

Area of minor segment OAB = (1225 × 3.14)/6 – (1225 × 1.732)/4

Area of minor segment OAB = (3846.5)/6 – (2121.7)/4

Area of minor segment OAB = 641.0833333 – 530.425

∴ Area of minor segment OAB = 110.65833333 cm² ...(ii)

Total area of design = 6 × Area of minor segment OAB

⇒ Total area of design = 6 × 110.65833333 (from ii)

∴ Total area of design = 663.95 cm²

Total area of design is 663.95 cm².

56. In the given figure, PQ = 24 cm, PR = 7 cm and 0 is the centre of the circle. Find the area of the shaded region. [Take = π = 3.14]

Solution

Here we will subtract the area of right angle triangle PQR and semicircle from the area of entire circle.

Given PQ = 24 cm, PR = 7 cm

Consider △PQR, ∠QPR = 90°

RQ² = PQ² + PR² (Pythagoras theorem)

RQ² = 24² + 7²

⇒ RQ² = 576 + 49

⇒ RQ2 = 625

∴ RQ = 25 cm

Therefore Radius of the circle = half of RQ

Let radius be ‘r’

r = 25/2

∴ r = 12.5 cm

Area △PQR = 1/2 ×base × height

Area of △PQR = 1/2 × PR × PQ

Area of △PQR = 1/2 × 7 × 24

Area of △PQR = 7 × 12

∴ Area of △PQR = 84 cm² ...(i)

Area of semicircle = πr²/2

Area of semicircle = (3.14 × (12.5²)/2 (putting π = 3.14)

Area of semicircle = (3.14 × 156.25)/2

∴ Area of semicircle = 245.3125 cm² ...(ii)

Area of circle = πr²

Area of circle = π(12.5²)

⇒ Area of circle = 3.14 × 156.25 (putting π = 3.14)

∴ Area of circle = 490.625 cm² ...(iii)

Area of shaded region = (iii) - (ii) - (i)

⇒ Area of shaded region = 490.625 – 245.3125 – 84

∴ Area of shaded region = 161.3125 cm²

Area of shaded region is 161.3125 cm².

57. In the given figure, △ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and 0 is the centre of the incircle of △ABC . [Take π = 3.14]

Solution

Given AB = 6 cm, BC = 10 cm

Consider △ABC, ∠BAC = 90°

BC² = AB² + AC² (Pythagoras theorem)

⇒ 10² = 6² + AC² (putting given values)

⇒ 100 = 36 + AC²

⇒ 100 – 36 = AC²

⇒ AC² = 64

∴ AC = 8 cm

Join OB, OA, OC, OE, OF, OD

Here OE = OF = OD = radius of circle = r cm

∠OEC = ∠ODB = ∠OFB = 90° (angle at the point of contact of radius & tangent)

Area △ABC = Area of △OAC + Area of △OCB + Area of △OAB ...(i)

Area of △OAC = 1/2 × OE × AC

Area of △OAC = 1/2 × r × 8

∴ Area of △OAC = 4r ...(ii)

Area of △OCB = 1/2 × OD × BC

 Area of △OCB = 1/2 × r × 10

∴ Area of △OCB = 5r ...(iii)

Area of △OAB = 1/2 × OF × AB

Area of △OAB = 1/2 × r × 6

∴ Area of △OAB = 3r ...(iv)

Area of △ABC = 1/2 × AB × AC

Area of △ABC = 1/2 × 6 × 8

⇒ Area of △ABC = 3 × 8

∴ Area of △ABC = 24 cm² ...(v)

Putting all the values in equation we get:

⇒ 24 = 4r + 5r + 3r

⇒ 24 = 12r

r = 24/12

∴ r = 2 cm

Area of circle = πr²

Put the value of r, we get,

⇒ Area of circle = π × 2²

⇒ Area of circle = 3.14 × 4 (putting π = 3.14)

∴ Area of circle = 12.56 cm² ...(vi)

Area of shaded region = Area of triangle – Area of circle

⇒ Area of shaded region = 24 – 12.56 (from v and vi)

∴ Area of shaded region = 11.44 cm²

Area of shaded region is 11.44 cm².

58. In the given figure, △ABC is right-angled at A. A semicircle are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.

Solution

Here we will first find out the area of semicircle whose diameter is BC and then subtract the area of right angle triangle ABC from it and then we will subtract this result from the area of semicircles whose diameters area AB and AC.

Consider △ABC, ∠BAC = 90°

BC² = AC² + AB² (Pythagoras theorem)

⇒ BC² = 4² + 3²

⇒ BC² = 16 + 9

⇒ BC² = 25

∴ BC = 5 cm

Area of semicircle = πr²/2 ...(i)

where r = radius of the semicircle

Area of semicircle whose diameter is AC.

Radius = AC/2

Radius = 4/2

∴ Radius = 2 cm

Area of semicircle = π(2)²/2 (from i)

∴ Area of semicircle = 2π cm²...(ii)

Area of semicircle whose diameter is AB

Radius = AB/2

Radius = 3/2

∴ Radius = 1.5 cm

Area of semicircle = π(1.5)²/2 (from i)

∴ Area of semicircle = 1.125π cm² ...(iii)

Area of semicircle whose diameter is BC

Radius = BC/2

Radius = 5/2

∴ Radius = 2.5 cm

Area of semicircle = π(2.5)²/2 (from i)

∴ Area of semicircle = 3.125π cm² ...(iv)

Area of triangle PQR = 1/2 × AB×AC

Area of triangle PQR = 1/2 × 3 × 4

⇒ Area of triangle PQR = 3 × 2

∴ Area of triangle PQR = 6 cm² ...(v)

Now subtract equation 5 from equation 4.

⇒ Area of semicircle excluding △ABC = (iv) - (v)

⇒ Area of semicircle excluding △ABC = 3.125π – 6

⇒ Area of semicircle excluding △ABC = 3.125 × 22/7 – 6 cm²

⇒ Area of semicircle excluding △ABC = (3.125 × 22)/7 – 6

⇒ Area of semicircle excluding △ABC = (68.75 – 42)/7

⇒ Area of semicircle excluding △ABC = (26.75)/7

∴ Area of semicircle excluding △ABC = 3.8214 cm² ...(vi)

Area of shaded region = (iii) + (ii) - (vi)

⇒ Area of shaded region = 2π + 1.125π – 3.8214

Area of shade region = 3.125π – 3.8214

Area of shaded region = 3.125 × 22/7 – 3.8214

Area of shaded region = 68.75/7 – 3.8214

⇒ Area of shaded region = 9.8214 – 3.8214

∴ Area of shaded region = 6 cm²

Area of shaded region 6 cm².

59. PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semicircles are drawn with PQ and QS as diameters, as shown in the given figure. If PS = 12 cm, find the perimeter and area of the shaded region. [Take π = 3.14]

Solution

Here we will subtract the area of semicircle whose diameter is QS from the area of the semicircle whose diameter PS and add the area of semicircle whose diameter is PQ so as to find out the area of the shaded region.

Given PS = 12 cm.

Radius of the circle = 6 cm

PQ = QR = RS

So, let PQ = QR = RS = k cm

Also, PQ + QR + RS = PS

⇒ k + k + k = 12

⇒ 3k = 12

k = 12/3

∴ k = 4 cm

So, PQ = QR = RS = 4 cm

Area of semicircle = πr²/2 -eqn1 where r = radius of the semicircle

Area and perimeter of semicircle whose diameter is PS

Radius = PS/2

Radius = 12/2

∴ Radius = 6 cm

Area of semicircle = π(6)²/2 (from i)

∴ Area of semicircle = 18π cm² ...(ii)

Perimeter of semicircle = πr

⇒ Perimeter of semicircle = π × 6

∴ Perimeter of semicircle = 6π cm ...(iii)

Area of semicircle whose diameter is QS

Radius = QS/2

Radius = 8/2

⇒ Radius = 4 cm

Area of semicircle = π(4)²/2 (from i)

∴ Area of semicircle = 8π cm² ...(iv)

Perimeter of semicircle = πr

⇒ Perimeter of semicircle = π × 4

∴ Perimeter of semicircle = 4π cm ...(v)

Area of semicircle whose diameter is PQ

Radius = PQ/2

Radius = 4/2

∴ Radius = 2 cm

Area of semicircle = π(2)²/2 (from i)

∴ Area of semicircle = 2π cm² ...(vi)

Perimeter of semicircle = πr

⇒ Perimeter of semicircle = π × 2

∴ Perimeter of semicircle = 2π cm ...(vii)

Area of the shaded region = eqn2 – eqn4 + eqn6

Area of shaded region = 18π - 8π + 2π

⇒ Area of shaded region = 12π

⇒ Area of shaded region = 12 × 3.14 (putting π = 3.14)

∴ Area of shaded region = 37.68 cm²

Perimeter of shaded region = (iii) - (v) + (vii)

 ⇒ Perimeter of shaded region = 6π - 4π + 2π

⇒ Perimeter of shaded region = 4π

⇒ Perimeter of shaded region = 4 × 3.14 (put π = 3.14)

∴ Perimeter of shaded region = 12.56 cm

Perimeter of the shaded region is 12.56 cm and Area of shaded region is 37.68 cm².

60. The inside perimeter of a running track shown in figure is 400 m. The length of each of the straight portion is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track. Also, find the length of the outer boundary of the track.

Solution

Consider the figure as a combination of two semicircles on the ends of the rectangle.

Let the length of rectangle be ‘L’ m and breadth be ‘B’ cm

Given L = 90 m, W = 14 m

Perimeter of running track = 400 m

Perimeter of inside of running track = 2L + Arc of two semicircles ...(i)

Arc length of a semicircle = πr where r = radius

⇒ 400 = (2 × 90) + (2 × πr) (putting values in eqn1)

⇒ 400 = 18 + 2πr

⇒ 400 - 180 = 2πr

⇒ 220 = 2πr

⇒ 220 = 2 × 22/7 × r (π = 22/7)

⇒ 220 = 44/7 × r

⇒ (220 × 7)/44 = r

∴ r = 35 m

Area of inner of running track = Area of rectangle + 2 × area of semicircles ...(ii)

Area of rectangle = L × B

Here B = 2r

B = 70 m

⇒ Area of inner rectangle = 90 × 70

∴ Area of inner rectangle = 6300 m² ...(iii)

Area of inner semicircles = 2 × πr²/2

Area of inner semicircles = 2 × π(35)²/2

⇒ Area of inner semicircles = 1225π

Area of inner semicircles = 1125 × 22/7

⇒ Area of inner semicircle = 175 × 22

∴ Area of inner semicircle = 3850 m² ...(iv)

Area of inner of running track = 6300 + 3850 (from 3& 4)

∴ Area of inner of running track = 10150 m²

Now radius of semicircles of outer of the running track = R = r + W

⇒ R = 35 + 14

∴ R = 49 m

Area of outer semicircles = 2 × πR²/2

Area of outer semicircles = 2 × π(49)²/2

⇒ Area of outer semicircles = 2401π

⇒ Area of outer semicircles = 2401 × 22/7

⇒ Area of outer semicircles = 343 × 22

∴ Area of outer semicircle = 7546 m² ...(v)

Breadth of outer running track = B’ = 2R

⇒ B’ = 2 × 49

∴ B’ = 98 m

Area of outer rectangle = L × B’

⇒ Area of outer rectangle = 90 × 98

∴ Area of outer rectangle = 8820 m² ...(vi)

Area of entire ground = 8820 + 7546 (from 5 & 6)

∴ Area of entire ground = 16366 m²

Area of running track = Area of entire ground – Area of inner ground

⇒ Area of running track = 16366 - 10150

∴ Area of running track = 6216 m²

Perimeter of outer boundary = 2L + Arc of outer semicircles

Arc length of an outer semicircle = πR, where R = outer radius

Perimeter of outer boundary = (2 × 90) + (2 × 22/7 × 49) (putting values)

⇒ Perimeter of outer boundary = 180 + (2 × 22 × 7)

⇒ Perimeter of outer boundary = 180 + 308

∴ Perimeter of outer boundary = 488 m

Area of running track is 6216 m² and perimeter of outer boundary is 488 m.