RD Sharma Solutions Chapter 9 Arithmetic Progression Exercise 9.3 Class 10 Maths

Chapter Name | RD Sharma Chapter 9 Arithmetic Progression |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 9.3 Solutions
1. Find:
(i) 10 th term of the AP 1, 4, 7, 10, .......
(ii) 18 th term of AP √2, 3√2, 5√2, .......
(iii) nth term of the AP 13, 8, 3, -2, ........
(iv) 10 th term of the AP -40, -15, 10, 35, .....
(v) 8 th term of the AP 11, 104, 91, 78, .......
(vi) 11 th term of the AP 10.0, 10.5, 11.0, 11.5, .....
(vii) 9 th term of the AP 3/4, 5/4, 7/4, 9/4 , ........
Solution
(i) Given A.P. is
1, 4, 7, 10, ......
First term (a) = 1
Common difference (d) = second term - first term
= 4 - 1 = 3
n th term in an A.P = a (n -1)d
10th term in an A.P = 1 + (10 - 1)3
= 1 + 9×3
= 1 + 27 = 28
(ii) Given, A.P is √2, 3√2, 5√2, .......
First term (a) = √2
common difference(d) = second term - first term
3√2 - √2 = 2√2
n th term in an A.P = a + (n -1)d
18 th term of A.P = √2 + (18 - 1)2√2
= √2 + 17 × 2√2
= √2(1 + 34)
= 35√2
(iii) Given, A.P is 13, 8, 3, -2, ........
First term (a) = 13
Common difference (d) = Second term - first term
8 - 13 = - 5
n th term of an A.P = a + (n -1)d
= 13 + (n -1) - 5
= 13 - 5n + 5
= 18 - 5n
(iv) Given A.P is
-40, -15, 10, 35, .......
First term (a) = -40
Common difference (d) = Second term - first term
= -15 - (-40)
= 40 - 15 = 25
n th term of an A.P = a + (n -1)d
10 th term of A.P = -40 + (10 - 1)25
= -40 + 9×25
= -40 + 225 = 185
(v) Given sequence is
117, 104, 91, 78, .........
First learn can = 117
Common difference (d) = Second term - first term
= 104 - 117 = - 13
n th term = a + (n -1)d
8 th term = a + (8 - 1)d
= 117 + 7(-13)
= 117 - 91 = 26
(vi) Given A.P is 10.0, 10.5, 11.0, 11.5, .....
First term (a) = 10.0
Common difference (d) = Second term - First term
= 10.5 - 10.0 = 0.5
n th term = a + (n - 1)d
11 th term = 10.0 + (11 - 1) 0.5
= 10.0 + 10 ×0.5
= 10.0 + 5= 15.0
(vii) Given A.P. is 3/4, 5/4, 7/4, 9/4 , ........
First term (a) = 3/4
Common difference (d) = Second term - First Term
= 5/4 - 3/4 = 2/4
n th term = a + (n - 1)d
9 th term = a + (9 -1)d
= 3/4 + 8× 2/4
= 3/4 + 16/4
= 19/4
2. (i) Which term of the AP 3, 8, 13, ..... is 248?
(ii) Which term of the AP 84, 80, 76, ...... is 0 ?
(iii) Which term of the AP 4, 9, 14, ...... is 254 ?
(iv) Which term of the AP 21, 42, 63, 84, ...... is 420?
(v) Which term of the AP 121, 117, 113, ...... is its first negative term ?
Solution
(i) Given A.P is 3, 8, 13, .....
First term (a) = 3
common difference (d) = Second term - first term
= 8 - 3 = 5
n th term (an ) = a + (n - 1)d
Given n th term an = 248
248 = 3 + (n - 1)5
⇒ 248 = -2 + 5n
⇒ 5n = 250
⇒ n = 250/5 = 50
50 th term is 248
(ii) Given A.P is 84, 80, 76, .......
First term (a) = 84
Common difference (d) = a2 - a
= 80 - 84 = -4
n th term (an ) = a + (n - 1)d
Given n th term is 0
0 = 84 + (n - 1)× -4
⇒ 0 = 84 -4(n - 1)
⇒ 4(n-1) = 84
⇒ n - 1= 84/4 = 21
⇒ n = 21 + 1= 22
⇒ 22 nd term is 0.
(iii) Given A.P. 4, 9, 14, ........
First term (a) = 4
Common difference (d) = a2 - a
= 9 - 4 = 5
n th term (an ) = a + (n -1)d
Given nth term is 254
4 + (n - 1)5 = 254
⇒ (n - 1)5 = 250
⇒ n - 1= 250/5 = 50
= 50 + 1 = 51
∴ 51 th term is 254.
(iv) Given A.P 21, 42, 63, 84, ......
a = 21, d = a2 - a
= 42 - 21 = 21
n th term (an ) = a + (n - 1)d
Given n th term = 420
21 + (n - 1)21 = 420
⇒ (n - 1)21 = 399
⇒ n - 1 = 399/21 = 19
⇒ n = 19 + 1 = 20
∴ 20 th term is 420.
(v) Given A.P is 121, 117, 113,........
First term (a) = 121
Common difference (d) = 117 - 121 = - 4
n th term (a) = a + (n - 1)d
Given n th term is negative i.e., an < 0
121 + (n - 1)-4 < 0
⇒ 121+ 4 - 4n < 0
⇒ 125 < 4n
⇒ n > 125/4
⇒ n > 31.25
The integer which comes after 31.25 is 32,
∴ 32 nd term is first negative term
3. (i) Is 68 a term of the AP 7, 10, 13, ...... ?
(ii) Is 302 a term of the AP 3, 8, 13,...... ?
(iii) Is -150 a term of the AP 11, 8, 5, 2, ...... ?
Solution
In the given problem, we are given an A.P and the value of one of its term
We need to find whether it is a term of the AP or not so here we will use the formula
an = a + (n - 1)d
(i) Here, AP is 7, 10, 13, ......
an = 68, a = 7, and d = 10 - 7 = 3
Using the above mentioned formula, we get
68 = 7 + (n - 1)3
⇒ 68 - 7 = 3n - 3
⇒ 31 + 3 = 3n
⇒ 64 = 3n
⇒ n = 64/3
Since, the value of n is a fraction.
Thus, 68 is not the team of the given A.P.
(ii) Here, AP is 3, 8, 13,....
an = 302, a = 3
d = 8 - 3= 5 using the above mentioned formula, we get
302 = 3 + (n -1)5
⇒ 302 - 3 = 5n - 5
⇒ 299 = 5n - 5
⇒ 5n = 304
⇒ n = 304/5
Since, the value of 'n' is a fraction. Thus, 302 is not the term of the given A.P.
(iii) Here, A.P. is 11, 8, 5, 2, ......
an = -150, a = 1 and d = 8 - 11= -3
Thus, using the above mentioned formula, we get
-150 = 11 + (n - 1)(-3)
⇒ -150 - 11 = -3n + 3
⇒ -161 - 3 = -3n
⇒ n = -164/-3
Since, the value of n is a fraction. Thus, -150 is not the term of the given A.P.
4. How many term are there in the AP ?
(i) 7, 10, 13,..... 43
(ii)-1, -5/6, -2/3, -1/2,........, 10/3
(iii) 7, 13, 19,...... 05
(iv) 18, 15(1/2), 13, ...... , -47
Solution
(i) 7, 10, 13,..... 43
From given A.P
a = 7, d = 10 - 7 = 3, an = a + (n - 1)d.
Let, an = 43 (last term)
7 + (n - 1)3 = 43
⇒ (n-1) = 39/3=13
⇒ n = 13
∴ 13 terms are there in given A.P.
(ii) -1, -5/6, -2/3, -1/2,........, 10/3
From given A.P
a = -1, d = -5/6 + 1 = 1/6
an = a + (n - 1)d
Let, an = 10/3 (last term)
-1 + (n - 1)1/6 = 10/3
⇒ (n - 1) × 1/6 = 13/3
⇒ n - 1 = (13 × 6)/3 = 26
⇒ n = 27
∴ 27 terms are there in given A.P.
(iii) 7, 13, 19, ....., 05
From the given A.P
a = 7, d = 13 - 7 = 6,
an = a + (n - 1)d
Let an = 205 (last term)
7 + (n - 1)6 = 205
⇒ (n - 1)6 = 205- 7 = 198
⇒ n -1 = 198/6 = 33
⇒ n = 33+ 1 = 34
∴ 34 terms are there in given A.P.
(iv) 18, 15(1/2), 13, ...... , -47
From the given A.P
a = 18, d = 31/2 - 18 = 15.5 - 18 = -2.5
an = a + (n - 1)d
Let an = -47(last term)
18 + (n - 1) × -2.5 = - 47
⇒ (n -1)× -2.5 = -47 - 18
⇒ n - 1= -65/-2.5
⇒ n - 1 = (65 × 10)/25 = 26
⇒ n = 26 + 1 = 27
∴ 27 terms are there in given A.P.
5. The first term of an AP is 5, the common difference is 3 and the last term is 80, find the number of terms.
Solution
Given
First term(a) = 5
Common difference (d) = 3
Last term (an ) = 80
To calculate no of terms in given A.P
an = a + (n - 1)d
Let an = 80,
80 = 5 + (n - 1)3
⇒ (n - 1)3 = 75
⇒ n - 1 = 75/3 = 25
⇒ n = 25 + 1 = 26
∴ There are 26 terms.
6. The 6th and 17 terms of an A.P are 19 and 41 respectively, find the 40th term.
Solution
Given, a6 = 19, a17 = 41
⇒ a6 = a + (6 - 1)d
19 = a + 5d ...(1)
an = a + (17 - 1)d
⇒ 41 = a + 16d ....(2)
Subtract (1) from (2)
a + 16d = 41 ...(1)
a + 5d = 19 ...(2)
11d = 22
⇒ d = 22/11 = 2
Substitute d = 2 in (1)
19 = a + 5(2)
a = 9
∴ 40 th term a40 = a + (40 - 1)d
= 9 + 39 × 2
= 9 + 78 = 87
∴ a40 = 87
7. If 9 th term of an A.P is zero, prove that its 29 th term is double the 19 th term.
Solution
Given
9th term of an A.P a9 = 0,
an = a + (n - 1)d
a + (a - 1)d = 0
⇒ a + 8d = 0
⇒ a = -8d
We have to prove
24th term is double the 19 th term a29 = 2 . a19
a + (29 - 1)d = 2[a + (19 - 1)d]
a + 28d = 2[a + 18d]
Put a = -8d
-8d + 28d = 2[-8d + 18d]
⇒ 20d = 2×10d
⇒ 20d = 20d
Hence proved
8. If 10 times the 10th term of an A.P is equal to 15 times the 15th term, show that 25th term of the A.P. is zero.
Solution
Given,
10 times of 10th term is equal to 15 times of 15th term.
10a10 = 15.a15
10[a + (10 - 1)d] = 15[a + (15 - 1)d] [∴ an = a + (n - 1)d]
⇒ 10(a + 9d) = 15(a + 14.d)
⇒ a + 9d = 15/10(a + 14d)
⇒ a - (3/2)a = 42d/2 - 9d
⇒ -1a/2 = (42d - 18d)/2
⇒ -a/2 = 24d/2 =12d
⇒ a = -24d
We have to prove 25 th term of A.P is 0
a25 = 0
⇒ a + (25 - 1)d = 0
⇒ a + 24d = 0
Put a = -24d
-24d + 24d = 0
⇒ 0 = 0
Hence proved.
9. The 10 th and 18 th terms of an A.P. are 41 and 73 respectively. Find 26 th term.
Solution
Given,
an = 41, an = 73,
an = a +(n - 1)d
⇒ a10 = a + (10 - 1)d
41 = a + 9d ...(1)
⇒ an = a + (18 - 1)d
73 = a + 17d ....(2)
Subtract (1) from (2)
a + 17d = 73 ...(1)
⇒ a + 9d = 41 ...(2)
⇒ 0 + 8d = 32
⇒ d = 32/8 = 4
Substitute d = 4 in (1)
a + 9×4 = 41
⇒ a = 41 - 36
⇒ a = 5
26 th term an = a + (26 - 1)d
= 5 + 25×4
= 5 + 100
= 105
∴ 26th term a26 = 105
10. In a certain A.P the 24 th term is twice the 10 th term. Prove that the 72 nd term is twice the 34 th term.
Solution
Given,
24 th term is twice the 10 th term
a24 = 2 a10
Let, first term of a square = a
Common difference = d
n th term an = a + (n - 1)d
a + (24 - 1)d = (a + (10 - 1)d)2
⇒ a + 23d = 2(a + 9d)
⇒ (23 - 18)d = a
⇒ a = 5d
We have to prove
72nd term is twice the 34 th term
a12 = 2a34
⇒ a + (12 - 1)d = 2[a + (34 - 1)d]
⇒ a + 71d = 2a + 66d
Substitute a = 5d
5d + 71d = 2(5d) + 66d
⇒ 76d = 10 d + 66d
⇒ 76d = 76d
Hence proved.
11. If (m + 1)th term of an A.P. is twice the (n + 1)th term, prove that (3m + 1) th term is twice the (m + n +1) th term.
Solution
Given,
(m + 1) th term is twice the (m + 1)th term.
First term = a
Common difference = d
n th term an = a + (n - 1)d
am+1 = 2an + 1
⇒ a + (m + 1 - 1)d = 2(a + (n + 1 - 1)d )
⇒ a + md = 2(a + nd)
⇒ a = (m - 2n)d
We have to prove
(3m + 1)th term is twice the (m + n + 1)th term
a3m + 1 = 2.am+n+1
⇒ a + (3m + 1 - 1)d = (a + (m + n + 1 -1).d)
⇒ a + 3m.d - 2a + 2(m + n)d
Substitute a = (m - 2n)d
(m - 2n)d + 3m d = 2(m - 2n)d + 2(m + n)d
⇒ 4m - 2n = 4m - 4n + 2n
⇒ 4m - 2n = 4m - 2n
Hence proved.
12. If the n term of the A.P 9, 7, 5, ........ is same as the term of the A.P. 15, 12, 9, ..... find n.
Solution
Given,
First sequence is 9,7,5, .......
a = 9, d = 7 - 9 = -2, an = a + (n + 1)d
an = 9 + (n - 1) × -2
Second sequence is 15, 12, 9, ......
a = 15, d = 12 - 15 = -3, an = a + (n - 1)d
an = 15 + (n - 1) × -3
Given an an are equal
9 -2(n - 1) = 15 - 3(n - 1)
⇒ 3(n - 1) - 2(n - 1) - 15 - 9
⇒ n - 1 = 6
⇒ n = 7
∴ 7th term of two sequence are equal.
13. Find the 12th term from the end of the following arithmetic progressions:
(i) 3, 5, 7, 9, .....201
(ii) 3, 8,13, ......, 253
(iii) 1, 4,7, 10, ...... 88
Solution
(i) 3, 5, 7, 9, ....., 201
First term (a) = 3
Common difference (d) = 5 - 3 = 2
12 th term from the end is can be considered as (l) last term = first term and common difference = d1 = -d
nth term from the end = last term + (n - 1)×-d
12 th term from end = 201 + (12 - 1)× -2
= 201 - 22
= 179
(ii) 3, 8, 13, ........,253
First term a = 3
Common difference d = 8 - 3 = 5
Last term (l) = 253
n th term of sequence on = a + (n - 1)d
To find nth term from the end, we put last term (l) as 'a' and common difference as -d
nth term from the end = last term + (n - 1) -d
12 th term from the end = 253 + (12 - 1) ×-5
= 253 - 55 = 198
∴ 12 th term from the end = 198
(iii) 1, 4, 7, 10, ......., 88
First term a = 1
Common difference d = 4 - 1 = 3
Last term (l) = 88
n th term an = a + (n + 1)d
n th term from the end = last term + (n - 1)-d
12 th term from the end = 88 + (12 - 1)× -3
= 88 - 33
= 55
∴ 12 th term from the end = 55
14. The 4 th term of an A.P is three times the first and the 7 term exceeds twice the third term by 1. Find the first term and the common difference.
Solution
Given,
4 th term of an AP is three times the times the first term
a4 = 3.a
n th term of a sequence an = a + (n - 1)d
a + (4 - 1)d = 3a
⇒ a + 3d = 3a
⇒ 3d = 2a
⇒ a = 3d/2 ...(1)
Seventh term exceeds twice the third term by 1.
a7 + 1 = 2a3
⇒ a + (7 - 1)d + 1 = 2[a+(3 -1)d]
⇒ a + 6d + 1 = 2a + 4d
⇒ 2a - a = 6d - 4d + 1
⇒ a = 2d + 1 ...(2)
By equating (1), (2)
3d/2 = 2d + 1
⇒ 3d/2 - 2d = 1
⇒ -d/2 = 1
⇒ d = -2
Put d = -2 in a = 3d/2
= (3/2)(-2)
= -3
∴ First term a = -3, common difference d = -2.
15. Find the second term and nth term of an A.P. whose 6 th term is 12 and the 8 th term is 22.
Solution
Given,
a6 = 12, a8 = 22
n th term of an A.P an = a + (n - 1)d
a6 = a + (6 - 1)d = a + 5d = 12 ...(1)
a8 = a+ (8 -1)d = a + 7d = 22 ...(2)
Subtracting (1) from (2)
2d = 10
⇒ d = 5
putting value of d in equation (1)
a + 5d = 12
⇒ a + 5×5 = 12
⇒ a = 12 - 25 = -13
Second term a2 = a + (2 - 1)d
=a + d
= -13 + 5 = -8
n th term an = a + (n - 1)d
= -13 + (n - 1)×5
= -13 + 5n - 5
= -18 + 5n
nth term an = a + (n - 1)d
= -13 + (n - 1)-5
an = -18 + 5n
∴ a2 = -8, an = -18 + 5n
16. How many number of two digits are divisible by 3 ?
Solution
We observe that 12 is the firs two - digit number divisible by 3 and 99 is the last two digit number divisible by 3. Thus, the sequence is
12, 15, 18,........, 99
This sequence is in A.P with
First term (a) = 12
Common difference(d) = 15 - 12 = 3
n th term an = 99
n th term of an A.P
(an ) = a + (n -1)d
99 = 12 +(n -1)3
⇒ 99 - 12 = (n - 1)3
⇒ 87/3 = n = 1
⇒ n = 30
∴ 30 term are there in the sequence.
17. An A.P. consists of 60 terms. If the first and the last terms be 7 and 125 respectively, find 32 nd term.
Solution
Given,
No. of terms = n = 60
First term (a) = 7
Last term (a) = 7
Last term (a10 ) = 125
an = a + (n - 1)d
⇒ a60 = a + (60 - 1)d
⇒ 125 = 7 + 59d
⇒ 118 = 59d
⇒ d = 118/59 = 2
52 nd term a32 = a + (32 - 1)d
= 7 + 31×2
= 7 + 62 = 69
18. The sum of 4 and 8th terms of an A.P. is 24 and the sum of the 6 th and 10 th terms is 34. Find the first term and the common difference of the A.P.
Solution
Given,
a4 + a8 = 24
a6 + a10 = 34
⇒ a + (4 - 1)d + a + (18 - 1)d = 24
2a + 10d = 24
a + 5d = 12 ....(1)
⇒ a6 + a10 = 34
a + (6 - 1)d + a + (10 - 1)d = 34
⇒ 2a + 14d = 34
a + 7d = 17 ....(2)
Subtract (1) from (2)
a + 7d = 17
⇒ a + 5d = 12
⇒ 2d = 5
⇒ d = 5/2
Put d = 5/2 in a + 5d = 12
a = 12 - 5d
⇒ a = 12 - 5× 5/2
⇒ a = 12 - 25/2 = -1/2
∴ a = -1/2, d = b/2
19. The first term of an A.P. is 5 and its 100 th term is - 292. Find the 50 th term of this A.P.
Solution
Given,
20. Find a30 - a20 for the A.P.
(i) -9, -14, -19, -24, .......
(ii) a, a +d, a + 2d, a + 3d, .......
Solution
Given,
21. Write the expression an - ak for the A.P. a, a + d, a + 2d, .......
Hence, find the common difference of the AP for which
(i) 11 th term an = 5 and 13 th term a13 = 79
(ii) a10 - a5 = 200
(iii) 20 th term is 10 more than the 18 th term.
Solution
General arithmetic progression
a, a + d, a+ 2d, .........
22. Find n if the given value of x is the n term of the given A.P.
(i) 1, 21/11, 31/11, 41/11, ........., x = 141/11
(ii) 5(1/2), 11, 16(1/2), 22, ........, x = 550
(iii) -1, -3, -5, -7, ........,x = -151
(iv) 25, 50,75, 100, .......,c = 1000


23. If an A.P. consists of n terms with first term a and nth term 1 show that the sum of the m th term from the beginnin and the m th term from the end is (a + 1).
Last term = 1
Total no. of terms = n
Common difference = d


a + (n - 1) = 32
⇒ a + (7 - 1)d = 32
⇒ a + 6d = 32 .......(1)

First term (a) = 3,
Common difference (d) = 10 - 3 = 7
Let, nth term of A.P will be 84 more than 13 th term

Hence 25 th term of given A.P is 84 more than 13 th term .

63, 65, 67,....... and 3, 10, ......

∴ 13 th term of both the sequence are equal.
250 - 2 = 248
248 is the last multiple of 4 before 250.
The sequence is
12, ......, 248
With first term (a) = 12
Last term (l) = 248
Common difference (d) = 4

∴ There are 60 terms between 10 and 250 which are multiples of 4.
105 is the first 3 digit number which is divisible by 7 when we divide 999 with 7 remainder is 5. So, 999 - 5 = 994 is the last three digits divisible by 7 so, the sequence is
105, ........, 994
First term (a) = 105
Last tem (l) = 994
Common difference (d) = -7
Let there are n numbers in the sequence
an = 994
⇒ a + (n - 1)d = 994
⇒ 105 + (n - 1)7 = 994
⇒ (n - 1)7 = 994 - 105 = 889
⇒ n - 1 = 889/7 = 127
⇒ n = 127 + 1 = 128
∴ there are 128 numbers between 105, 994, which are divisible by 7.
8, 14, 20, 26,.......
Let n th term is 72 more than its 41 st term
For the given sequence
a = 8, d = 14 - 8 = 6
⇒ a + (n - 1)d = 8 + (n -1)6 + 72
⇒ 8 + (n - 1)6 = 8 + 40×6 + 72
⇒ (n - 1)6 = 312
⇒ n - 1 = 312/6 = 52
⇒ n = 52+1 = 53
∴ 53 rd term is 72 more than 41 st term
For this a = 9, d = 12 - 9 = 3
Let nth term is 39 more than its 36 th term

a = 7, d = 10 - 7 = 3, l = 184
n th term from the end = l + (n - 1) -d
8 th term from the end = 184 + (8 - 1)× - 3
= 184 - 21 = 163
∴ 8 th term from the end - 163.
a = 8, d = 10 - 8 = 2, l = 126
n th term from the end = l+ (n -1)× -d
10 th term from the end = 126 + (10 - 1) × -2
= 126 -18
= 108
∴ 10 th term from the end = 108
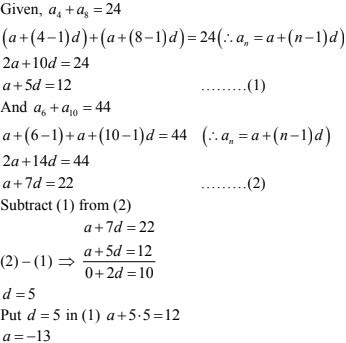
Given, A.P. is
3, 15, 27, 39, .......
Let n th termis 120 more than 21 st term

17 th term of an A.P is 5 more than twice its 8 th term




