RS Aggarwal Solutions Chapter 4 Triangles MCQ Class 10 Maths

Chapter Name | RS Aggarwal Chapter 4 Triangles |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
MCQ for Triangles Class 10 Maths
1. A man goes 24m due west and then 10m due both. How far is he from the starting point?
(a) 34m
(b) 17m
(c) 26m
(d) 28m
Solution
(c) 26 m
Suppose, the man starts from point A and goes 24 m due west to point B. From here, he goes 10 m due north and stops at C.
In right triangle ABC, we have:
AB = 24 m, BC = 10 m
Applying Pythagoras theorem, we get:
AC2 = AB2 + BC2 = 242 + 102
AC2 = 576 + 100 = 676

(a) 9m
(b) 10m
(c) 11m
(d) 12m
Solution
(b) 10 m

Let AB and DE be the two poles.
According to the question:
AB = 13 m
DE = 7 m
Distance between their bottoms = BE = 8 m
Draw a perpendicular DC to AB from D, meeting AB at C. We get:
DC = 8m, AC = 6 m
Applying, Pythagoras theorem in right-angled triangle ACD, we have
AD2 = DC2 + AC2
= 82 + 62 = 64 + 36 = 100

(a) 2.4m
(b) 1.35m
(c) 1.5m
(d) 13.5m
Solution
Let AB and AC be the vertical stick and its shadow, respectively.
According to the question:
AB = 1.8 m
AC = 45 cm = 0.45 m
Again, let DE and DF be the pole and its shadow, respectively.
According to the question:
DE = 6 m
DF = ?
Now, in right-angled triangles ABC and DEF, we have:
∠BAC = ∠EDF = 90°
∠ACB = ∠DFE (Angular elevation of the sun at the same time)
Therefore, by AA similarity theorem, we get:
∆ABC ~ ∆DFE
⇒ AB/AC = DE/DF
⇒ 1.8/0.45 = 6/DF
⇒ DF = (6 × 0.45)/1.8 = 1.5 m
4. A vertical pole 6m long casts a shadow of length 3.6m on the ground. What is the height of a tower which casts a shadow of length 18m at the same time?
(a) 10.8m
(b) 28.8m
(c) 32.4m
(d) 30m
Solution
(d)

Let AB and AC be the vertical pole and its shadow, respectively.
According to the question:
AB = 6 m
AC = 3.6 m
Again, let DE and DF be the tower and its shadow.
According to the question:
DF = 18 m
DE =?
Now, in right -angled triangles ABC and DEF, we have:
∠BAC = ∠EDF = 90°
∠ABC = ∠DFE = (Angular elevation of the sun at the same time)
Therefore, by AA similarity theorem, we get:
∆ABC - ∆DEF
⇒ AB/AC = DE/DF
⇒ 6/(3.6) = DE/18
⇒ DE = (6 × 18)/3.6 = 30 m
5. The shadow of a 5m long stick is 2m long. At the same time the length of the shadow of a 12.5m high tree(in m) is
(a) 3.0
(b) 3.5
(c) 4.5
(d) 5.0
Solution

Suppose DE is a 5 m long stick and BC is a 12.5 m high tree.
Suppose DA and BA are the shadows of DE and BC respectively.
Now, In ∆ABC and ∆ADE
∠ABC = ∠ADE = 90°
∠A = ∠A (Common)
By AA- similarity criterion
∆ABC~ ∆ADE
If two triangles are similar, then the ratio of their corresponding sides are equal.
∴ AB/AD = BC/DE
⇒ AB/2 = (12.5)/5 cm
⇒ AB = 5 cm
Hence, the correct answer is option (d).
6. A ladder 25m long just reaches the top of a building 24m high from the ground. What is the distance of the foot of the ladder from the building?
(a) 7m
(b) 14m
(c) 21m
(d) 24.5m
Solution
(a) 7 m

Let the ladder BC reaches the building at C.
Let the height of building where the ladder reaches be AC.
According to the question:
BC = 25 m
AC = 24 m
In right-angled triangle CAB, we apply Pythagoras theorem to find the value of AB.
BC2 = AC2 + AB2
⇒ AB2 = BC2 – AC2 = 252 – 242
⇒ AB2 = 625 – 576 = 49


Now, In right triangle MOP
By using Pythagoras theorem, we have
MP2 = PO2 + OM2
= 122 + 162
= 144 + 256
= 400
∴ MP2 = 400
⇒ MO = 20 cm
Now, In right triangle MPN
By using Pythagoras theorem, we have
PN2 = NM2 + MP2
= 212 + 202
= 441 + 400
= 841
∴ MP2 = 841
⇒ MP = 29 cm
Hence, the correct answer is option (b).
8. The hypotenuse of a right triangle is 25cm. The other two sides are such that one is 5cm longer than the other. The lengths of these sides are
(a) 10cm, 15cm
(b) 15cm, 20cm
(c) 12cm, 17cm
(d) 13cm, 18cm
Solution
(b) 15 cm, 20 cm
It is given that length of hypotenuse is 25 cm.
Let the other two sides be x cm and (x−5) cm.
Applying Pythagoras theorem, we get:
252 = x2 + (x − 5 )2
⇒ 625 = x2 + x2 + 25 – 10x
⇒2x2 – 10x − 600 = 0
⇒ x2 – 5x − 300 = 0
⇒ x2 – 20x + 15x − 300 = 0
⇒ x(x − 20) + 15(x − 20) = 0
⇒ (x – 20) (x + 15) = 0
⇒ x − 20 = 0 or x + 15 = 0
⇒ x = 20 or x = −15
Side of a triangle cannot be negative.
Therefore, x = 20 cm
Now,
x – 5 = 20 – 5 = 15 cm
9. The height of an equilateral triangle having each side 12cm, is
(a) 6√2 cm
(b) 6√3m
(c) 3√6m
(d) 6√6m
Solution
(b) 6√3 cm

Let ABC be the equilateral triangle with AD as its altitude from A.
In right-angled triangle ABD, we have
AB2 = AD2 + BD2
AD2 = AB2 − BD2
= 122 − 62
= 144 – 36 = 108

(a) 12cm
(b) 16cm
(c) 18cm
(d) 24cm
Solution
(d) 24 cm

In triangle ABC, let the altitude from A on BC meets BC at D.
We have:
AD = 5 cm, AB = 13 cm and D is the midpoint of BC.
Applying Pythagoras theorem in right-angled triangle ABD, we get:
AB2 = AD2 + BD2
⇒ BD2 = AB2 – AD2
⇒ BD2 = 132 − 52
⇒ BD2 = 169 − 25
⇒ BD2 = 144

Therefore, BC = 2BD = 24 cm
11. In a ∆ABC, it is given that AB = 6cm, AC = 8cm and AD is the bisector of ∠A. Then, BD:DC = ?
(a) 3 : 4
(b) 9 : 16
(c) 4 : 3
(d) √3 : 2

Solution
(a) 3 : 4
In ∆ ABD and ∆ACD, we have:
∠BAD = ∠CAD
Now,
BD/DC = AB/AC = 6/8 = 3/4
BD : DC = 3 : 4
12. In ∆ABC, it is given that AD is the internal bisector of ∠A. If BD = 4cm, DC = 5cm and AB = 6cm, then AC = ?
(a) 4.5cm (b) 8cm (c) 9cm (d) 7.5cm

Solution
(d) 7.5 cm
It is given that AD bisects angle A
Therefore, applying angle bisector theorem, we get:
BD/DC = AB/AC
⇒ 4/5 = 6/x
⇒ x = (5 × 6)/4 = 7.5
Hence, AC = 7.5 cm
13. In a ∆ABC, it is given that AD is the internal bisector of ∠A. If AB = 10cm, AC = 14cm and BC = 6cm, then CD = ?
(a) 4.8cm (b) 3.5cm (c) 7cm (d) 10.5cm

By using angle bisector in ∆ABC, we have
AB/AC = BD/DC
⇒ 10/14 = (6 – x)/x
⇒ 10x = 84 – 14x
⇒ 24x = 84
⇒ x = 3.5
Hence, the correct answer is option (b).
14. In a triangle, the perpendicular from the vertex to the base bisects the base. The triangle is
(a) right-angled
(b) isosceles
(c) scalene
(d) obtuse-angled
Solution
(b) Isosceles
In an isosceles triangle, the perpendicular from the vertex to the base bisects the base.
15. In an equilateral triangle ABC, if AD ⊥ BC, then which of the following is true?
(a) 2AB2 = 3AD2
(b) 4AB2 = 3AD2
(c) 3AB2 = 4AD2
(d) 3AB2 = 2AD2
Solution
(c) 3AB2 = 4AD2
Applying Pythagoras theorem in right-angled triangles ABD and ADC, we get:
AB2 = AD2 + BD2
⇒ AB2 = (1/2AB)2 + AD2 (∵ ∆ABC is equilateral and AD = 1/2AB)
⇒ AB2 = 1/4AB2 + AD2
⇒ AB2 – 1/4AB2 = AD2
⇒ 3/4AB2 = AD2
⇒ 3AB2 = AD2
16. In a rhombus of side 10cm, one of the diagonals is 12cm long. The length of the second diagonal is
(a) 20cm
(b) 18cm
(c) 16cm
(d) 22cm
Solution
(c) 16 cm

Let ABCD be the rhombus with diagonals AC and BD intersecting each other at O. Also, diagonals of a rhombus bisect each other at right angles.
If AC = 12 cm, AO = 6 cm
Applying Pythagoras theorem in right-angled triangle AOB. We get:
AB2 = AO2 + BO2
⇒ BO2 = AB2 − AO2
⇒ BO2 = 102 − 62 = 100 − 36 = 64

⇒ BD = 2 × BO = 2 × 8 = 16 cm
Hence, the length of the second diagonal BD is 16 cm.
17. The lengths of the diagonals of a rhombus are 24cm and 10cm. The length of each side of the rhombus is
(a) 12cm
(b) 13cm
(c) 14cm
(d) 17cm
Solution
(b) 13 cm

Let ABCD be the rhombus with diagonals AC and BD intersecting each other at O.
We have:
AC = 24 cm and BD = 10 cm
We know that diagonals of a rhombus bisect each other at right angles.
Therefore applying Pythagoras theorem in right-angled triangle AOB, we get:
AB2 = AO2 + BO2 = 122 + 52
= 144 + 25 = 169

Hence, the length of each side of the rhombus is 13 cm.
18. If the diagonals of a quadrilateral divide each other proportionally, then it is a
(a) parallelogram
(b) trapezium
(c) rectangle
(d) square
Solution
(b) trapezium
Diagonals of a trapezium divide each other proportionally.
19. The line segments joining the midpoints of the adjacent sides of a quadrilateral form
(a) parallelogram
(b) trapezium
(c) rectangle
(d) square
Solution
(a) A parallelogram
The line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
20. If the bisector of an angle of a triangle bisects the opposite side, then the triangle is
(a) scalene
(b) equilateral
(c) isosceles
(d) right-angled
Solution
(c) isosceles
Let AD be the angle bisector of angle A in triangle ABC.
Applying angle bisector theorem, we get:
AB/AC = BD/DC
It is given that AD bisects BC.
Therefore, BD = DC
⇒ AB/AC = 1
⇒ AB = AC
Therefore, the triangle is isosceles.
21. In the given figure, ABCD is a trapezium whose diagonals AC and BD intersect at O such that OA = (3x – 1) cm, OB = (2x + 1)cm, OC = (5x – 3)cm and OD = (6x – 5)cm. Then, x = ?
(a) 2
(b) 3
(c) 2.5
(d) 4

(a) 2
We know that the diagonals of a trapezium are proportional.
Therefore OA/OC = OB/OD
⇒ (3X – 1) (6X – 5) = (2X + 1) (5X - 3)
⇒ 18X2 – 15X – 6X + 5 = 10X2 – 6X + 5X – 3
⇒ 18X2 – 21X + 5 = 10X2 – X – 3
⇒ 18X2 – 21X + 5 – 10X2 + X + 3 = 0
⇒ 8X2 – 20X + 8 = 0
⇒ 4(2X2 – 5X + 2) = 0
⇒ 2X2 – 5X + 2 = 0
⇒ 2X2 – 4X – X + 2 = 0
⇒ 2X(X – 2) – 1(X – 2) = 0
⇒ (X – 2)(2X – 1) = 0
⇒ Either x – 2 or 2x – 1 = 0
⇒ Either x = 2 or x = ½
When x = 1/2, 6x – 5 = -2 < 0, which is not possible.
Therefore, x = 2
22. In ∆ABC, it is given that AB/AC = BD/DC. If ∠B = 70° and ∠C = 50°, then ∠BAD = ?
(a) 30°
(b) 40°
(c) 45°
(d) 50°
Solution
(a) 30°
We have:
AB/AC = BD/DC
Applying angle bisector theorem, we can conclude that AD bisects ∠A.
In ∆ABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A = 180 − ∠B − ∠C
⇒ ∠A = 180 − 70 − 50 = 60°
∵ ∠BAD = ∠CAD = 1/2∠BAC
∴ ∠BAD = ½ × 60 = 30°
23. In ∆ABC, DE║BC so that AD = 2.4cm, AE = 3.2cm and EC = 4.8cm. Then, AB = ?
(a) 3.6cm
(b) 6cm
(c) 6.4cm
(d) 7.2cm
Solution
(b) 6 cm
It is given that DE || BC.
Applying basic proportionality theorem, we have:
AD/BD = AE/EC
⇒ 2.4/BD = 3.2/4.8
⇒ BD = (2.4 × 4.8)/3.2 = 3.6 cm
Therefore, AB = AD + BD = 2.4 + 3.6 = 6 cm
24. In a ∆ABC, if DE is drawn parallel to BC, cutting AB and AC at D and E respectively such that AB = 7.2cm, AC = 6.4cm and AD = 4.5cm. Then, AE = ?
(a) 5.4cm
(b) 4cm
(c) 3.6cm
(d) 3.2cm
Solution
(b) 4cm
It is given that DE || BC.
Applying basic proportionality theorem, we get:
AD/AB = AE/AC
⇒ 4.5/7.2 = AE/AC
⇒ AE = (4.5 × 6.4)/7.2 = 4 cm
25. In ∆ABC, DE ║ BC so that AD = (7x – 4)cm, AE = (5x – 2)cm, DB = (3x + 4)cm and EC = 3x cm. Then, we have:
(a) x = 3
(b) x = 5
(c) x = 4
(d) x = 2.5
Solution
(c) x = 4
It is given DE || BC.
Applying Thales’ theorem. We get:
AD/BD = AE/EC
⇒ (7x – 4)/(3x + 4) = (5x – 2)/3x
⇒ 3x(7x – 4) = (5x – 2)(3x + 4)
⇒ 21x2 – 12x = 15x2 + 20x – 6x – 8
⇒ 21x2 – 12x = 15x2 + 14x – 8
⇒ 6x2 – 26x + 8 = 0
⇒ 2(3x2 – 13x + 4) = 0
⇒ 3x2 – 13x + 4 = 0
⇒ 3x2 – 12x – x + 4 = 0
⇒ 3x(x – 4) – 1(x – 4) = 0
⇒ (x – 4)(3x – 1) = 0
⇒ x – 4 = 0 or 3x – 1 = 0
⇒ x – 4 or x = 1/3
If x = 1/3, 7x – 4 = -5/3 < 0; it is not possible.
Therefore, x = 4
26. In ∆ABC, DE ║ BC such that AD/DB = 3/5. If AC = 5.6 cm, AE = ?
(a) 4.2cm
(b) 3.1cm
(c) 2.8cm
(d) 2.1cm
Solution
(d) 2.1 cm
It is given that DE || BC.
Applying Thales’ theorem, we get:
AD/DB = AE/EC
Let AE be x cm.
Therefore, EC = (5.6 – x) cm
⇒ 3/5 = x/(5.6 – x)
⇒ 3(5.6 – x) = 5x
⇒ 16.8 – 3x = 5x
⇒ 8x = 16.8
⇒ x = 2.1 cm
27. ∆ABC~∆DEF and the perimeters of ∆ABC and ∆DEF are 30cm and 18cm respectively. If BC = 9cm, then EF = ?
(a) 6.3cm
(b) 5.4cm
(c) 7.2cm
(d) 4.5cm
Solution
(b) 5.4 cm
∆ABC ~ ∆DEF
Therefore,
Perimeter(∆ABC)/Perimeter(∆DEF) = BC/EF
⇒ 30/18 = 9/EF
⇒ EF = (9 × 18)/30 = 5.4 cm
28. ∆ABC~∆DEF such that AB = 9.1cm and DE = 6.5cm. If the perimeter of ∆DEF is 25cm, what is the perimeter of ∆ABC?
(a) 35cm
(b) 28cm
(c) 42cm
(d) 40cm
Solution
(a) 35 cm
∵ ∆ABC ~ ∆DEF
∴ Perimeter(∆ABC)/Perimeter(∆DEF) = AB/DE
⇒ Perimeter(∆ABC)/25 = (9.1)/(6.5)
⇒ Perimeter (∆ABC) = (9.1 × 25)/6.5 = 35 cm
29. In ∆ABC, it is given that AB = 9cm, BC = 6cm and CA = 7.5cm. Also, ∆DEF is given such that EF = 8cm and ∆DEF~∆ABC. Then, perimeter of ∆DEF is
(a) 22.5cm
(b) 25cm
(c) 27cm
(d) 30cm
Solution
(d) 30 cm
Perimeter of ∆ABC = AB + BC + CA = 9 + 6 + 7.5 = 22.5 cm
∵ ∆DEF ~ ∆ABC
∴ Perimeter(∆ABC)/Perimeter(∆DEF) = BC/EF
⇒ 22.5/Perimeter(∆DEF) = 6/8
Perimeter(∆DEF) = (22.5 × 8)/6 = 30 cm
30. ABC and BDE are two equilateral triangles such that D is the midpoint of BC. Ratio of these area of triangles ABC and BDE is
(a) 2 : 1
(b) 1 : 4
(c) 1 : 2
(d) 4 : 1
Solution
Give: ABC and BDE are two equilateral triangles
Since, D is the midpoint of BC and BDE is also an equilateral triangle.
Hence, E is also the midpoint of AB.
Now, D and E are the midpoint of BC and AB.
In a triangle, the line segment that joins midpoint of the two sides of a triangle is parallel to the third side and is half of it.
DE ǁ CA and DE = ½.CA
Now, in ∆ABC and ∆EBD
∠BED = ∠BAC (Corresponding angles)
∠B = ∠B (Common)
By AA-similarity criterion
∆ABC ~ ∆EBD
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴ area(∆ABC)/area(∆DBE) = (AC/ED)2 = (2ED/ED)2 = 4/1
Hence, the correct answer is option (d).
31. It is given that ∆ABC~∆DEF. If ∠A = 30°, ∠C = 50°, AB = 5cm, AC = 8cm and DF = 7.5cm, then which of the following is true?
(a) DE = 12cm, ∠F = 50°
(b) DE = 12cm, ∠F = 100°
(c) DE = 12cm, ∠D = 100°
(d) EF = 12cm, ∠D = 30°
Solution
(b) DE = 12 cm, ∠F = 100°
Disclaimer: In the question, it should be ∆ABC ~ ∆DFE instead of ∆ABC ~ ∆DEF.
In triangle ABC,
∠A + ∠B + ∠C = 180°
∴ ∠B = 180 − 30 − 50 = 100°
∵ ∆ABC ~ ∆DFE
∴ ∠D = ∠A = 30°
∠F = ∠B = 100°
And ∠E = ∠C = 50°
Also,
AB/DF = AC/DE
⇒5/7.5 = 8/DE
⇒ DE = (8 × 7.5)/2 = 12 cm
32. In the given figure, ∠BAC = 90° and AD⊥BC. Then,

(a) BC.CD = BC2
(b) AB.AC = BC2
(c) BD.CD = AD2
(d) AB.AC = AD2
Solution
(c) BD. CD = AD2
In ∆ BDA and ∆ADC, we have:
∠BDA = ∠ADC = 90°
∠ABD = 90° − ∠DAB
= 90° − (90° − ∠DAC)
= 90° − 90° + ∠DAC
= ∠DAC
Applying AA similarity, we conclude that ∆BDA − ∆ADC.
⇒ BD/AD = AD/CD
⇒ AD2 = BD.CD
33. In ΔABC, AB = 6√3, AC = 12 cm and BC = 6cm. Then ∠B is
Solution
AB = 6√3 cm
⇒ AB2 = 108 cm2
AC = 12 cm
⇒ AC2 = 144 cm2
BC = 6 cm
⇒ BC2 = 36 cm
∴ AC = AB2 + BC2
Since, the square of the longest side is equal to the sum of two sides, so ∆ABC is a right angled triangle.
∴ The angle opposite to ∠90°
Hence, the correct answer is option (c)
34. In ∆ABC and ∆DEF, it is given that AB/DE = BC/FD, then
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A = ∠F
Solution
(c) ∠B = ∠D
Disclaimer: In the question, the ratio should be AB/DE = BC/FD = AC/EF
We can write it as:
AB/ED = BC/DF = AC/FE
Therefore, ∆ ABC − EDF
Hence, the corresponding angles, i.e., ∠B ∠D, will be equal.
i.e., ∠B = ∠D
35. In ∆DEF and ∆PQR, it is given that ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
(a) EF/PR = DF/PQ
(b) DE/PQ = EF/RP
(c) DE/QR = DF/PQ
(d) EF/RP = DE/QR
Solution
(b) DE/PQ = EF/RP
In ∆DEF and ∆PQR, we have:
∠D = ∠Q and ∠R = ∠E
Applying AA similarity theorem, we conclude that ∆DEF ~ ∆QRP.
Hence, DE/QR = DE/QP = EF/PR
36. If ∆ABC~∆EDF and ∆ABC is not similar to ∆DEF, then which of the following is not true
(a) BC.EF = AC.FD
(b) AB.EF = AC.DE
(c) BC.DE = AB.EF
(d) BC.DE = AB.FD
Solution
(c) BC. DE = AB. EF
∆ABC ~ ∆EDF
Therefore,
AB/DE = AC/EF = BC/DF
BC. DE ≠ AB. EF
37. In ∆ABC and ∆DEF, it is given that ∠B = ∠E, ∠F = ∠C and AB = 3DE, then the two triangles are
(a) congruent but not similar
(b) similar but not congruent
(c) neither congruent nor similar
(d) similar as well as congruent
Solution
(b) similar but not congruent
In ∆ABC and ∆DEF, we have:
∠B = ∠E and ∠F = ∠C
Applying AA similarity theorem, we conclude that ∆ABC - ∆DEF.
Also,
AB = 3DE
AB ≠ DE
Therefore, ∆ABC and ∆DEF are not congruent.
38. If in ∆ABC and ∆PQR, we have: AB/QR = BC/QR = CA/PQ, then
(a) ∆PQR ~ ∆CAB
(b) ∆PQR ~ ∆ABC
(c) ∆CBA ~ ∆PQR
(d) ∆BCA ~ ∆PQR
Solution
(a) ∆PQR ~ ∆CAB
In ∆ABC and ∆PQR, we have:
AB/QR = BC/PR = CA/PQ
⇒ ∆ABC ~ ∆QRP
We can also write it as ∆PQR ~ ∆CAB.
39. In the given figure, two line segment AC and BD intersect each other at the point P such that PA = 6cm, PB = 3cm, PC = 2.5cm, PD = 5cm, ∠APB = 50°and ∠CDP = 30°, then ∠PBA = ?
(a) 50°
(b) 30°
(c) 60°
(d) 100°

(d) 100°
In ∆ APB and ∆ DPC, we have:
∠APB = ∠DPC = 50°
AP/BP = 6/3 = 2
DP/CP = 5/2.5 = 2
Hence, AP/BP = DP/CP
Applying SAS theorem, we conclude that ∆APB - ∆DPC.
∴ ∠PBA = ∠PCD
In ∆ DPC, we have:
∠CDP + ∠CPD + ∠PCD = 180°
⇒ ∠PCD = 180° − ∠CDP − ∠CPD
⇒ ∠PCD = 180° − 30° − 50°
⇒ ∠PCD = 100°
Therefore, ∠PBA = 100°
40. Corresponding sides of two similar triangles are in the ratio 4:9 Areas of these triangles are in the ration
(a) 2:3
(b) 4:9
(c) 9:4
(d) 16:81
Solution
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴ (area of first triangle)/(area of second triangle)
= (Side of first triangle)/(Side of second triangle)2
= (4/9)2
= 16/81
Hence, the correct answer is option (d).
41. It is given that ∆ABC~∆PQR and BC/QR = 2/3, then ar(∆PQR)/ar(∆ABC) = ?
(a) 2/3
(b) 3/2
(c) 4/9
(d) 9/4
Solution
(d) 9:4
It is given that ∆ABC ~ ∆PQR and BC/QR = 2/3
Therefore,
ar(∆PQR)/ar(∆ABC) = QR2/BC2 = (3/2)2 = 9/4
42. In an equilateral ∆ABC, D is the midpoint of AB and E is the midpoint of AC. Then, ar(∆ABC) : ar(∆ADE) = ?
(a) 2 : 1
(b) 4 : 1
(c) 1 : 2
(d) 1 : 4

(b) 4:1
In ∆ABC, D is the midpoint of AB and E is the midpoint of AC.
Therefore, by midpoint theorem,
Also, by Basic Proportionality Theorem,
AD/DB = AE/EC
Also,
AB = AC = BC (∵ ∆ABC is an equilateral triangle)
So, AD/DB = AE/EC = 1
In ∆ABC and ∆ADE, we have:
∠A = ∠A
AD/DB = AE/AC = 1/2
∴ ∆ ABC - ∆ADE (SAS criterion)
∴ ar(∆ABC) ∶ ar(∆ADE) = (AB)2 ∶ (AD)2
⇒ ar(∆ABC) : ar (∆ADE) = 22 : 12
⇒ ar(∆ABC) : ar(∆ADE) = 4: 1
43. In ∆ABC and ∆DEF, we have: AB/DE = BC/EF = AC/DF = 5/7, then ar(∆ABC) : ∆(DEF) = ?
(a) 5 : 7
(b) 25 : 49
(c) 49 : 25
(d) 125 : 343
Solution
(b) 25 :49
In ∆ABC and ∆DEF, we have:
AB/DE = BC/EF = AC/DE = 5/7
Therefore, by SSS criterion, we conclude that ∆ABC ~ ∆DEF.
⇒ ar(∆ABC)/ar(∆DEF) = AB2/DE2 = (5/7)2 = 25/49 = 25: 49
44. ∆ABC~∆DEF such that ar(∆ABC) = 36cm2and ar(∆DEF) = 49cm2. Then, the ratio of their corresponding sides is
(a) 36 : 49 (b) 6 : 7 (c) 7 : 6 (d) √6 : √7
Solution
(b) 6:7
∵ ∆ABC ~ ∆DEF
∴ AB/DE = BC/EF = AC/DF ...(i)
Also,
ar(∆ABC)/ar(∆DEF) = AB2/DE2
⇒ 36/49 = AB2/DE2
⇒ 6/7 = AB/DE
⇒ AB/DE = BC/EF = AC/DF = 6/7 (from (i))
Thus, the ratio of corresponding sides is 6 : 7.
45. Two isosceles triangles have their corresponding angles equal and their areas are in the ratio 25: 36. The ratio of their corresponding heights is
(a) 25 : 36
(b) 36 : 25
(c) 5 : 6
(d) 6: 5
Solution
(c) 5:6
Let x and y be the corresponding heights of the two triangles.
It is given that the corresponding angles of the triangles are equal.
Therefore, the triangles are similar. (By AA criterion)
Hence,
ar(∆1)/ar(∆2) = 25/36 = x2/y2
⇒ x2/y2 = 25/36
46. The line segments joining the midpoints of the sides of a triangle form four triangles, each of which is
(a) congruent to the original triangle
(b) similar to the original triangle
(c) an isosceles triangle
(d) an equilateral triangle
Solution
(b) similar to the original triangle
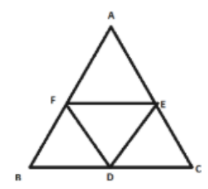
The line segments joining the midpoint of the sides of a triangle form four triangles, each of which is similar to the original triangle.
47. If ∆ABC~∆QRP, ar(∆ABC)/ar(∆QRP) = 9/4, AB = 18cm and BC = 15cm, then PR = ?
(a) 18 cm
(b) 10 cm
(c) 12 cm
(d) 20/3 cm
Solution
(b) 10 cm
∵ ∆ABC ~ ∆QRP
∴ AB/QR = BC/PR
Now,
ar(∆ABC)/ar(∆QRP) = 9/4
⇒ (AB/QR)2 = 9/4
⇒ AB/QR = BC/PR = 3/2
Hence, 3PR = 2BC = 2 × 15 = 30
PR = 10 cm
48. In the given figure, O is the point of intersection of two chords AB and CD such that OB = OD and ∠AOC = 45°. Then, ∆OAC and ∆ODB are
(a) equilateral and similar
(b) equilateral but not similar
(c) isosceles and similar
(d) isosceles but not similar
Solution
(c) isosceles and similar
In ∆AOC and ∆ODB, we have:
∠AOC = ∠DOB (Vertically opposite angles)
and ∠OAC = ∠ODB (Angles in the same segment)
Therefore, by AA similarity theorem, we conclude that ∆AOC − ∆DOB.
⇒ OC/OB = OA/OD = AC/BD
Now, OB = OD
⇒ OC/OA = OB/OD = 1
⇒ OC = OA
Hence, ∆OAC and ∆ODB are isosceles and similar.
49. In an isosceles ∆ABC, if AC = BC and AB2 = 2AC2, then ∠C = ?
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution
(d) 90°
Given:
AC = BC
AB2 = 2AC2 = AC2 + AC2 = AC2 + BC2
Applying Pythagoras theorem, we conclude that ∆ABC is right angled at C. Or, ∠C = 90°
50. In ∆ABC, if AB = 16cm, BC = 12cm and AC = 20cm, then ∆ABC is
(a) acute-angled
(b) right-angled
(c) obtuse-angled
Solution
(b) right-angled
We have:
AB2 + BC2 = 162 + 122 = 256 + 144 = 400
and, AC2 = 202 = 400
∴ AB2 + BC2 = AC2
Hence, ∆ABC is a right-angled triangle.
51. Which of the following is a true statement?
(a) Two similar triangles are always congruent
(b) Two figures are similar if they have the same shape and size.
(c) Two triangles are similar if their corresponding sides are proportional.
(d) Two polygons are similar if their corresponding sides are proportional.
Solution
(c) Two triangles are similar if their corresponding sides are proportional.
According to the statement:
∆ABC~ ∆DEF
if AB/DE = AC/DF = BC/EF
52. Which of the following is a false statement?
(a) If the areas of two similar triangles are equal, then the triangles are congruent. (b) The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
(c) The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding.
(d) The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Solution
(b) The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
Because the ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
53. Match the following:
Column I | Column II |
(a) In a given ∆ABC, DE ║BC and AD/DB = 3/5. If AC = 5.6 cm, then AE = ............... cm. (b) If ∆ABC~∆DEF such that 2AB = 3DE and BC = 6cm, then EF = ....…….cm. (c) If ∆ABC~∆PQR such that ar(∆ABC) : ar(∆PQR) = 9 : 16 and BC = 4.5cm, then QR = ……..cm. (d) In the given figure, AB║CD and OA = (2x + 4)cm, OB = (9x – 21)cm, OC = (2x – 1)cm and OD = 3cm. Then x = ?  | (p) 6 (q) 4 (r) 3 (s) 2.1 |
The correct answer is :
(a) -........
(b)-.........
(c) -.........
(d)-.........
Solution
(a) −(s)
Let AE be x.
Therefore, EC = 5.6 –x
It is given that DE || BC.
Therefore, by B.P.T., we get:
AD/DB = AE/EC
⇒ 3/5 = x/(5.6 – x)
⇒ 3(5.6 – x) = 5x
⇒ 16.8 – 3x = 5x
⇒ 8x = 16.8
⇒ x = 2.1 cm
(b) −(q)
∵ ∆ABC-∆DEF
∴ AB/DE = BC/EF
⇒ 3/2 = 6/EF
EF = (6 × 2)/3 = 4 cm
(c) −(p)
∵ ∆ABC ~ ∆PQR
∴ ar(∆ABC)/ar(∆PQR)
∴ ar(∆ABC)/ar(∆PQR) = BC2/QR2
⇒ 9/16 = (4.5)2/QR2

(d) –(r)
∵ AB|| CD
∴ OA/OB = OC/OD (Thales’ theorem)
⇒ (2x + 4)/(9x – 21) = (2x – 1)/3
3(2x + 4) = (2x – 1)(9x – 21)
⇒ 6x + 12 = 18x2 – 42x – 9x + 21
⇒ 18x2 – 57x + 9 = 0
⇒ 6x2 – 19x + 3 = 0
⇒ 6x2 – 18x – x + 3 = 0
⇒ (6x – 1)(x – 3) = 0
⇒ x = 3 or x = -1/6
But x = - 1/6 makes (2x – 1) < 0, which is not possible.
Therefore, x = 3
54. Match the following columns:
Column I | Column II |
(a) A man goes 10m due east and then 20m due north. His distance from the staring point is ……..m. (b) In an equilateral triangle with each side 10 cm, the altitude is ……… cm. (c) The area of an equilateral triangle having each side 10 cm is ……….. cm2. (d) The length of a diagonal of a rectangle having length 8 m and breadth 6 m is ……..m. | (p) 25√3 (q) 5√3 (r) 10√5 (s) 10 |
The correct answer is:
(a) -..........
(b) -.........
(c) -.........
(d) -..........
Solution

(a) −(r)
Let the man starts from A and goes 10 m due east at B and then 20 m due north at C. Then, in right-angled triangle ABC, we have:
AB2 + BC2 = AC2
Hence, the man is 10√3 m away from the starting point.

(b) −(q)
Let the triangle be ABC with altitude AD.
In right-angled triangle ABC, we have:
AB2 = AD2 + BD2
⇒ AD2 = 102 – 52 (∵ BD = ½ BC)


(c) – (p)
Area of an equilateral triangle with side a = √3/4.a2 = √3/4 × 102 = √3 × 5 × 5 = 25√3 cm2
(d) – (s)
Let the rectangle be ABCD with diagonals AC and BD.
In right-angled triangle ABC, we have:
AC2 = AB2 + BC2 = 82 + 62 = 64 + 36

Exercise – Formative Assessment
1. ∆ABC ~ ∆DEF and the perimeters of ∆ABC and ~ ∆DEF are 32cm and 24cm respectively. If AB = 10cm, then DE = ?
(a) 8cm
(b) 7.5cm
(c) 15cm
(d) 5√3cm
Solution
(b) 7.5 cm
∵ ∆ABC ~ ∆DEF
∴ Perimeter(∆ABC)/Perimeter(∆DEF) = AB/DE
⇒ 32/24 = 10/DE
⇒ DE = (10 × 24)/32 = 7.5 cm
2. In ∆ABC, DE║BC. If DE = 5cm, BC = 8cm and AD = 3.5cm, then AB = ?
(a) 5.6cm
(b) 4.8cm
(c) 5.2cm
(d) 6.4cm
Solution
(a) 5.6 cm
∵ DE ‖ BC
∴ AD/DB = AE/AC = DE/BC (Thales’ theorem)
⇒ 3.5/AB = 5/8
⇒ AB = (3.5×8)/5 = 5.6 cm
3. Two poles of heights 6m and 11m stand vertically on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
(a) 12m
(b) 13m
(c) 14m
(d) 15m
Solution
(b) 13 m

Let the poles be and CD
It is given that:
AB = 6 m and CD = 11 m
Let AC be 12 m
Draw a perpendicular farm Bon CD, meeting CD at E
Then,
BE = 12m
We have to find BD.
Applying Pythagoras theorem in right-angled BED, we have:
BD2 = BE2 + ED2
= 122 + 52 (∵ ED = CD – CE = 11 – 6)
= 144 + 25 = 169
BD = 13 m
4. The areas of two similar triangles are 25 cm2 and 36cm2 respectively. If the altitude of the first triangle is 3.5 cm, then the corresponding altitude of the other triangle.
(a) 5.6 cm
(b) 6.3 cm
(c) 4.2 cm
(d) 7 cm
Solution
We know that the ratio of the areas of similar triangles is equal to the squares of their corresponding altitudes.
Let h be the altitude of the other triangle.
Therefore,
25/36 = (3.5)2/h2
⇒ h2 = (3.5)2 × 3.6
⇒ h2 = 17.64
⇒ h = 4.2 cm
5. If ∆ABC ~∆DEF such that 2AB = DE and BC = 6 cm, find EF.
Solution
∵ ∆ABC ~∆DEF
∴ AB/DE = BC/EF
⇒ 1/2 = 6/EF
⇒ EF = 12 cm
6. In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.
Solution
∵ DE ║ BC
∴ AD/DB = AE/EC (Basic proportionality theorem)
x/(3x + 4) = (x + 3)/(3x + 19)
⇒ x(3x + 19) = (x + 3)(3x + 4)
⇒ 3x2 + 19x = 3x2 + 4x + 9x + 12
⇒ 19x – 13x = 12
⇒ 6x = 12
⇒ x = 2

Solution
Let the ladder be AB and BC be the height of the window from the ground.
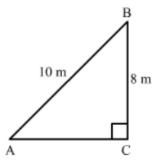
We have:
AB = 10 cm and BC = 8 m
Applying theorem in right-angled ACB, we have:
AB2 = AC2 + BC2
⇒ AC2 = AB2 – BC2 = 102 – 82
= 100 – 64
= 36
⇒ AC = 6 m
Hence, the ladder is 6 m away from the base of the wall.
8. Find the length of the altitude of an equilateral triangle of side 2a cm.
Solution
Let the triangle be ABC with AD as its altitude. Then, D is the midpoint of BC.
In right-angled triangle ABD, we have:

AB2 = AD2 + DB2
⇒ AD2 = AB2 – DB = 4a2 – a2 (∵ BD = 1/2BC)
= 3a2
AD = √3a
Hence, the length of the altitude of an equilateral triangle of side 2a cm is √3a cm.
9. ∆ABC~∆DEF such that (∆ABC) = 64 cm2 and ar(∆DEF) = 169 cm2. If BC = 4 cm, find EF.
Solution
∵ ∆ABC~∆DEF
∴ ar(∆ABC)/ar(∆DEF) = BC2/EF2
⇒ 64/169 = 42/EF2
⇒ EF2 = (16 × 169)/64
⇒ EF = (4 × 13)/8 = 6.5 cm
10. In a trapezium ABCD, it is given that AB ║ CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(∆AOB) = 84 cm2. Find ar(∆COD).
Solution
In ∆AOB and ∆COD, we have:

∠AOB = ∠COD (Vertically opposite angles)
∠OAB = ∠OCD (Alternate angles as AB║CD)
Applying AA similarity criterion, we get:
∆AOB -∆COD
∴ ar(∆AOB)/ar(∆COD) = AB2/CD2
⇒ 84/ar(∆COD) = (AB/CD)2
⇒ 84/ar(∆COD) = (2CD/CD)2
⇒ ar(∆COD) = 84/2 = 21 cm2
11. The corresponding sides of two similar triangles are in the Ration 2: 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
Solution
It is given that the triangles are similar.
Therefore, the ratio of areas of similar triangles will be equal to the ratio of squares of their corresponding sides.
∴ 48/(Area of larger triangle) = 22/32
⇒ 48/(Area of larger triangle) = 4/9
⇒ Area of larger triangle = (48 × 9)/4 = 108 cm2
12. In the given figure, LM ║CB and LN║CD. Prove that AM/AB = AN/AD.
Solution
LM ║ CB and LN║CD
Therefore, applying Thales’ theorem, we have:
AB/AM = AC/AL and AD/AN = AC/AL
⇒ AB/AM = AD/AN
∴ AM/AB = AN/AD

13. Prove that the internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
Solution
Let the triangle be ABC with AD as the bisector ∠A which meets BC at D.
We have to prove:
BD/DC = AB/AC

Draw CE║DA, meeting BA produced at E.
CD║ DA
Therefore,
∠2 = ∠3 (Alternate angles)
and ∠1 = ∠4 (Corresponding angles)
But,
∠1 = ∠2
Therefore,
∠3 = ∠4
⇒ AE = AC
In ∆BCE, DA ║ CE.
Applying Thales’ theorem, we have:
BD/DC = AB/AE
⇒ BD/DC = AB/AC
This completes the proof.
14. In an equilateral triangle with side a, prove that area = √3/4a2.
Solution

Let ABC be the equilateral triangle with each side to a.
Let AD be the altitude from A, meeting BC at D.
Therefore, D is the midpoint of BC.
Let AD be h.
Applying Pythagoras theorem in right-angled ABD, we have:
AB2 = AD2 + BD2
⇒ a2 = h2 + (a/2)2
⇒ h2 = a2 – a2/4 = 3/4a2
⇒ h = √3/2.a
Therefore,
Area of triangle ABC = 1/2 × base × height
= 1/2 × a × √3/2.a
This completes the proof.
15. Find the length of each side of a rhombus whose diagonals are 24 cm and 10 cm long.
Solution

Let ABCD be the rhombus with diagonals AC and BD intersecting each other at O.
We know that the diagonals of a rhombus bisect each other at right angles.
∴ If AC = 24 cm and BD = 10 cm, AO = 12 cm and BO = 5 cm
Applying Pythagoras theorem in right-angled triangle AOB, we get:
AB2 = AO2 + BO2 = 122 + 52 = 144 + 25 = 169
AB = 13 cm
Hence, the length of each side of the given rhombus is 13 cm.
16. Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
Solution
Let the two triangles be ABC and PQR.
We have:
∆ABC~∆PQR,
Here,
BC = a, AC = b and AB = c
PQ = r, PR = q and QR = p
We have to prove:
a/p = b/q = c/r = (a + b + c)/(p + q + r)
∆ABC~∆PQR; therefore, their corresponding sides will be proportional.
⇒ a/p = b/q = c/r = k (say) ...(i)
⇒ a = kp, b = kq and c = kr
∴ (Perimeter of ∆ABC)/(Perimeter of ∆PQR)
= (a + b + c)/(p + q + r)
= (kp + kq + kr)/(p + q + r) = k ...(ii)
From (i) and (ii), we get:
a/p = b/q = c/r = (a + b + c)/(p + q + r) = (Perimeter of ∆ABC)/(Perimeter of ∆PQR)
This completes the proof.
17. In the given figure, ∆ABC and ∆DBC have the same base BC. If AD and BC intersect at O.
prove that ar(∆ABC)/ar(∆DBC) = AO/DO.

Solution

Construction: Draw AX ⊥ CO and DY ⊥ BO.
As,
ar(∆ABC)/ar(∆DBC) = (1/2 × AX × BC)/(1/2 × DY × BC)
⇒ ar(∆ABC)/ar(∆DBC) = AX/DY ...(i)
In ∆ABC and ∆DBC, ∠AXY = ∠DYO = 90° (By construction)
∠AOX = ∠DOY (Vertically opposite angles)
∴ ∆AXO~∆DYO (By AA criterion)
∴ AX/DY = AO/DO (Thales’ theorem) ...(ii)
From (i) and (ii), we have:
ar(∆ABC)/ar(∆DBC)
= AX/DY = AO/DO or, ar(∆ABC)/ar(∆DBC) = AO/DO
This completes the proof.
18. In the given, XY ║ AC and XY divides ∆ABC into two regions, equal in area. Show that AX/AB = (2 - √2)/2
Solution
In ∆ABC and ∆BXY, we have:

∠B = ∠B
∠BXY = ∠BAC (Corresponding angles)
Thus, ∆ABC - ∆BXY (AA criterion)
∴ ar(∆ABC)/ar(∆BXY) = AB2/BX2 = AB2/(AB – AX)2 ...(i)
Also,
ar((∆ABC)/ar(∆BXY) = 2/1 {∴ ar(∆BXY) = ar(trapezium AXYV)} ...(ii)
From (i) and (ii), we have:
AB2/(AB – AX)2 = 2/1
⇒ AB/(AB – AX) = √2
⇒ (AB – AX)/AB = 1/√2
⇒ 1 – AX/AB = 1/√2

= (2 - √2)/2
19. In the given figure, ∆ABC is an obtuse triangle, obtuse-angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC.BD.
Solution
Applying Pythagoras theorem in right-angled triangle ADC, we get:

⇒ AC2 – DC2 = AD2
⇒ AD2 = AC2 – DB2 ...(1)
Applying Pythagoras theorem in right-angled triangle ADB, we get:
AB2 = AD2 + DB2
⇒ AB2 – DB2 = AD2
⇒ AD2 = AB2 – DB2 ...(2)
From equation (1) and (2), we have:
AC2 – DC2 = AB2 – DB2
⇒ AC2 = AB2 + DC2 – DB2
⇒ AC2 = AB2 + (DB + BC)2 – DB2 (∵ DB + BC = DC)
⇒ AC2 = AB2 + DB2 + BC2 + 2DB.BC – DB2
⇒ AC2 = AB2 + BC2 + 2BC.BD
This completes the proof.
20. In the given figure, each one of PA, QB and RC is perpendicular to AC. If AP = x, QB = z, RC = y, AB = a and BC = b, show that 1/x + 1/y = 1/z.

Solution
In ∆PAC and ∆QBC, we have:
∠A = ∠B (Both angles are 90°)
∠P = ∠Q (Corresponding angles)
And
∠C = ∠C (common angles)
Therefore, ∆PAC~∆QBC
AP/BQ = AC/BC
⇒ x/2 = (a + b)/b
⇒ a + b = ay/z ...(1)
In ∆RCA and ∆QBA, we have:
∠C = ∠B (Both angles are 90°)
∠R = ∠Q (corresponding angles)
And
∠A = ∠A (Common angles)
Therefore, ∆RCA~∆QBA
RC/BQ = AC/AB
⇒ y/z = (a + b)/2
⇒ a + b = ay/z ...(2)
From equation (1) and (2), we have:
bx/z = ay/z
⇒ bx = ay
⇒ a/b = x/y ...(3)
Also,
x/z = (a + b)/b
⇒ x/z = a/b + 1
Using the value of a/b from equation (3), we have:
⇒ x/z = x/y + 1
Dividing both sides by x, we get:
1/z = 1/y + 1/x
∴ 1/x + 1/y = 1/z
This completes the proof.



