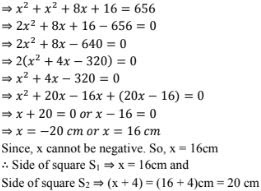RD Sharma Solutions Chapter 8 Quadratic Equations Exercise 8.11 Class 10 Maths

Chapter Name | RD Sharma Chapter 8 Quadratic Equations |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 8.11 Solutions
1. The perimeter of a rectangular field is 82m and its area is 400 m2 . Find the breadth of the rectangle.
Solution
Let the breadth of the rectangle be x meters
Given that,
Perimeter = 82 m and Area = 400 m2
We know that
Perimeter of a rectangle = 2(length + breadth)
⇒ 82 = 2(length + x)
⇒ 41 = length + x
⇒ length = (41 - x)m

2. The length of a hail is 5m more than its breadth. If the area of the floor of the hail is 84 m2 , what are the length and breadth of the hail ?
Solution
Let the breadth of the rectangle (hall) be x meter.
Given that,
Length of the hall is 5 m more than its breadth i.e., length = (x + 5)m
Since, x cannot be negative. So, breadth of the hall = 7m
Hence, length of the hall = (x + 5)m = (7 + 5)m = 12m.
3. Two squares have sides x cm and (x + 4)cm. The sum of their areas is 656 cm2 . Find the sides of the squares.
Solution
Let S1 and S2 be two squares
Let x cm be the side of square S1 and (x + 4) cm be the side of square S2 .
We know that,
Area of a square = (side)2
⇒ Area of square S1 = (x)2 = x2 cm2
⇒ Area of square S2 = (x + 4)2 cm2
Given that,
Area of square S1 + Area of square S2 = 656 cm2
⇒ x2 cm2 + (x + 4)cm2 = 656 cm2
4. The area of a right angled triangle is 165 m2 . Determine its base and altitude if the latter exceeds the former by 7 m.
Solution
Let the altitude of the right angled triangle be denoted by x meter
Given that altitude exceeds the base of the triangle by 7m.
⇒ Base = (x - 7)m
Since, x cannot be negative. So, x = 22 m
∴ Altitude of the triangle ⇒ x = 22 m
And base of the triangle ⇒ (x - 7)m = (22 - 7)m = 15m
5. Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m2 ? If so, find its length and breadth.
Solution
Let the breadth of the rectangular mango grove be x meter.
Given that length is twice that of breadth ⇒ length = 2×x m = 2x m
Given that area of the grove is 800 m2 .
Since, x cannot be a negative value.
So, x = 20 m
∴ Breadth of the mango grove = 20 m and length of the mango grove
= 2x m = 2×20 = 40 m
Yes. It is possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m2.
6. Is it possible to design a rectangular park of perimeter 80 m and area 400 m2 ? If so, find its length and breadth.
Solution
To prove the given condition, let us assume that the length of the rectangular park be denoted by x m.
Given that
Perimeter = 80m and
Area = 400 m2
We know that,
Perimeter of a rectangle = 2(length + breadth)
∴ Length of the rectangular park ⇒ x = 20 m and breadth of the rectangular park ⇒ (40 -x)m = (40 - 20)m = 20m
Yes, it is possible to design a rectangular park of perimeter 80m and area 400m2.
7. Sum of the areas of two squares is 640 m2 . If the difference of their perimeters is 64 m, find the sides of the two squares.
Solution
Let the two squares be denoted as S1 and S2 and let side of squares S1 be denoted as x meter and that of square S2 by y m.
Given that,
Difference of their perimeter is 64m.
We know that
Perimeter of a square = 4×side
⇒ Perimeter of a square S1 = 4 × x m = 4x m
⇒ Perimeter of square S2 = 4 × y m = 4y m
Now, difference of perimeter = perimeter of square S1 - Perimeter of square S2
⇒ 64m = (4x - 4y)m
⇒ 64 = 4(x - y)
⇒ x - y = 16
⇒ x = y + 16
And also,
Given that sum of areas of two squares = 640 m2 .
We know that,
Area of a square = (Side)2
⇒ Area of square S1 = x2 m2 .
⇒ Area of square S2 = y2 m2
Now,
Sum of areas of two squares = Area of square S1 + Area of square S2
Since, y cannot be a negative value, So, y = 8m
∴ Side of the square S2 is y = 8m
And side of the square S1 is x = (y + 16)m = (8 + 16)m = 24 m
Hence, sides of the two squares is 24m and 8m.