RD Sharma Solutions Chapter 5 Trigonometric Ratios Exercise 5.1 Class 10 Maths

Chapter Name | RD Sharma Chapter 5 Trigonometric Ratios |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 5.1 Solutions
1. In each of the following one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
Solution












2. In a ΔABC, right angled at B, AB = 24 cm, BC = 7cm. Determine
(i) SinA, CosA
(ii) SinC, CosC
(i) SinA, CosA
(ii) SinC, CosC
Solution
ΔABCis right angled at B
AB = 24cm, BC = 7cm.
AB = 24cm, BC = 7cm.

3. In Fig below, Find tan P and cot R. Is tan P = cot R?

Solution

4. If sin A = 9/41, compute cosA and tanA
Solution

5.Given 15 cotA = 8, find Sin A and secA.
Solution
15 cot A = 8, find Sin A and sec A

6. In ΔPQR, right angled at Q, PQ = 4 cm and RQ = 3 cm. Find the values of sin P, sin R, sec P and sec R.
Solution
ΔPQR, right angled at Q.

7. If cot θ =7/8, evaluate :
(i) [(1 + sinθ)(1 - sinθ)]/[(1 + cosθ)(1 - cosθ)
(ii) Cot2θ
(ii) Cot2θ
Solution

8. If 3cotA = 4, check whether (1 - tan2A)/(1 + tan2A) = cos2A - sin2A or not.
Solution

Solution

10. If 3 tanθ = 4, find the value of (4cosθ - sinθ)/(2cosθ + sinθ).
Solution

11. If 3cotθ = 2, find the value of = (4sinθ - 3cosθ)/(2sinθ + 6sinθ)
Solution

12. If tanθ = a/b, prove that (a sinθ - b cosθ)/(a sinθ + b cosθ) = (a2 - b2)/(a2 + b2).
Solution

13. If secθ = 13/5, show that (2cosθ - 3cosθ)/(4sinθ - 9cosθ) = 3
Solution
14. If cosθ = 12/13, show that sinθ (1 - tanθ) = 35/156 .
Solution

15. If cotθ = 1/√3, show that (1 - cos2θ)/(2 - sin2θ) = 3/5 .
Solution

16. If tanθ = 1/√7
(cosec2θ - sec2θ)/(cosec2θ + sec2θ) = 3/4
(cosec2θ - sec2θ)/(cosec2θ + sec2θ) = 3/4
Solution

17. If Sinθ = 12/13 find (sin2θ - cos2θ)/(2 sinθ cosθ) × 1/tan2θ
Solution

18. If secθ = 5/4 , find the value of (sinθ - 2cosθ)/(tanθ - cotθ)
Solution

19. Tanθ = 12/13
Find (2sinθ cosθ)/(cos2θ - sin2θ)
Find (2sinθ cosθ)/(cos2θ - sin2θ)
Solution

21. If cosθ = 3/5, find the value of (sinθ - 1/tanθ)/2tanθ .
Solution

22. If sinθ = 3/5, evaluate (cosθ - 1/tanθ)/2cotθ
Solution

23. If sec A = 5/4, verify that (3sinA - 4sin3A)/(4cos3A - 3cos A) = (3tanA - tan3A)/(1 - 3tan2A).
Solution

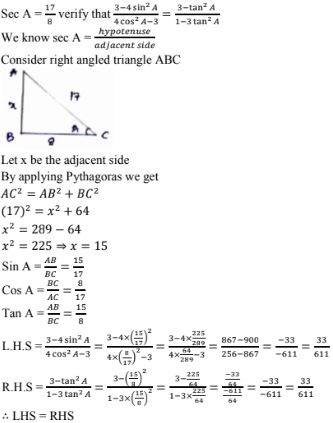
24. If sec A = 17/8, verify that (3 - 4sin2A)/(4cos2A - 3) = (3 - tan2A)/(1 - 3tan2A)
Solution
25. If cot θ = 3/4, prove that √(secθ - cosecθ)/(secθ + cosecθ) = 1/√7
Solution

27. If tanθθ = 24/7, find that sin θ + cos θ
Solution

28. If sin θ = a/b, find sec θ + tanθ in terms of a and b.
Solution

29. If 8 tan A = 15, find sinA - cosA.
Solution

30. If 3cosθ - 4sinθ = 2cosθ + sinθ Find tanθ .
Solution
3cosθ - 2cosθ = 4sinθ + sinθ find tanθ
3cosθ - 2cosθ = sinθ + 4sinθ
cosθ = 5sinθ
Dividing both side by use we get
cosθ/cosθ = 5sinθ/cosθ
1 = 5tanθ
⇒ tanθ = 1
31. If tanθ = 20/21, show that (1- sinθ + cosθ)/(1 + sinθ + cosθ) = 3/7
Solution

32. If Cosec A = 2 find 1/tanA + sinA/(1 + cosA)
Solution
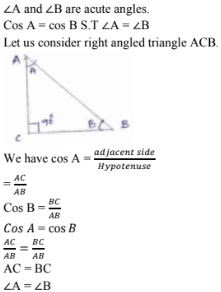
33. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution
34. If ∠A and ∠P are acute angles such that tan A = tan P, then show that ∠A = ∠P.
Solution
A and P are acute angle tan A = tan P
S.T. ∠A = ∠P
Let us consider right angled triangle ACP,

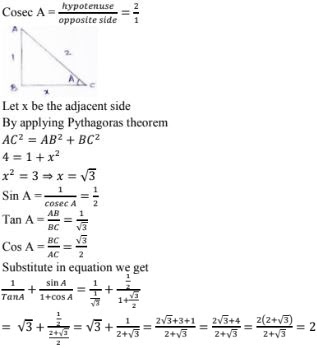
35. In a ΔABC, right angled at A, if tan C = √3, find the value of sin B cos C + cos B sin C .
Solution
In a Δle ABC right angled at A tan C = √3
Find sin B cos C + cos B sin C
Find sin B cos C + cos B sin C

36. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than I.
(ii) Sec A = 12/5 for some value of angle A.
(iii) Cos A is the abbreviation used for the cosecant of angle A.
(iv) Sin θ = 4/3 for some angle θ.
(i) The value of tan A is always less than I.
(ii) Sec A = 12/5 for some value of angle A.
(iii) Cos A is the abbreviation used for the cosecant of angle A.
(iv) Sin θ = 4/3 for some angle θ.
Solution
(a) Tan A ∠1
Value of tan A at 45° i.e., tan 45 = 1
As value of A increases to 90°
Tan A becomes infinite
So given statement is false.
(b) Sec A = 12/5 for some value of angle of
M - I
Sec A = 2.4
Sec A > 1
So given statement is True
M - II
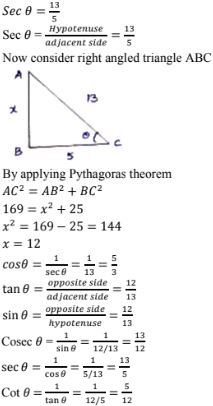
For sec A = 12/5
For sec A = 12/5 we get adjacent side = 13
M - I
Sec A = 2.4
Sec A > 1
So given statement is True
M - II
For sec A = 12/5
For sec A = 12/5 we get adjacent side = 13

We get a right angle Δle
Subtending 9i at B.
So, given statement is true.
Subtending 9i at B.
So, given statement is true.
(c) Cos A is the abbreviation used for cosecant of angle A.
The given statement is false
∴ Cos A is abbreviation used for cos of angle A but not for cosecant of angle A.
∴ Cos A is abbreviation used for cos of angle A but not for cosecant of angle A.
(d) Cot A is the product of cot A and A
Given statement is false
∵ cot A is co - tangent of angle A and co - tangent of angle A = (adjacent side)/(opposite side)
(e) Sin θ = 4/3 for some angle θ
Given statement is false
Since value of sin θ is less than (or) equal to one. Here value of sin θ exceeds one, so given statement is false.
Given statement is false
∵ cot A is co - tangent of angle A and co - tangent of angle A = (adjacent side)/(opposite side)
(e) Sin θ = 4/3 for some angle θ
Given statement is false
Since value of sin θ is less than (or) equal to one. Here value of sin θ exceeds one, so given statement is false.
