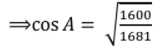RS Aggarwal Solutions Chapter 5 Trigonometric Ratios Exercise -5 Class 10 Maths
Chapter Name | RS Aggarwal Chapter 5 Trigonometric Ratios |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 5 Solutions
1. If sin θ = √3/2, find the value of all T- ratios of θ
Solution
Let us first draw a right ∆ABC, right angled at B and ∠C = θ
Now, we know that sin θ = Perpendicular/Hypotenuse
= AB/AC
= √3/2
So, if AB = √3k, then AC = 2k, where k is a positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ BC2 = AC2 – AB2 = (2k)2 – (√3k)2
⇒ BC2 = 4k2 – 3k2 = k2
⇒ BC = k
Now, finding the other T-rations using their definitions, we get:
cos θ = BC/AC = k/2k = 1/2
tan θ = AB/BC = √3k/k = √3
∴ cot θ = 1/tan θ = 1/√3,
cosec θ = 1/sin θ = 2/√3
sec θ = 1/cos θ = 2
2. If cos θ = 7/25, find the value of all T-ratios of θ
Solution
Let us first draw a right ∆ABC, right angled at B and ∠C = θ.
Now, we know that cos θ = Base/hypotenuse = BC/AC = 7/25
So, if BC = 7k, then AC = 25k, were k is a positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ AB2 = AC2 – BC2 = (25k)2 – (7k)2
⇒ AB2 = 625k2 – 49k2 = 576k2
⇒ AB = 24k
Now, finding the trigonometric ratios using their definitions, we get:
sin θ = AB/AC = 24k/25k = 24/25
tan θ = AB/BC = 24k/7k = 24/7
∴ cot θ = 1/tan θ = 7/24,
cosec θ = 1/sin θ = 25/24
sec θ = 1/cos θ = 25/7
3. If tan θ = 15/8, find the values of all T-ratios of θ
Solution
Let us first draw a right ∆ABC, right angled at B and ∠C = θ
Now, we know that tan θ = Perpendicular/Base = AB/BC = 15/8
So, if BC = 8k, then AB = 15k where k is positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2 = (15k)2 + (8k)2
⇒ AC2 = 225k2 + 64k2 = 289k2
⇒ AC = 17k
Now, finding the other T-ratios using their definitions, we get:
Sin θ = AB/AC = 15k/17k = 15/17
cos θ = BC/AC = 8k/17k = 8/17
∴ cot θ = 1/tan θ = 8/15,
cosec θ = 1/sin θ = 17/15
sec θ = 1/cos θ = 17/8
4. If cot θ = 2 find all the values of all T-ratios of θ
Solution
Let us first draw a right ∆ABC, right angled at B and ∠C = θ
Now, we know that cot θ = Base/Perpendicular = BC/AB = 2
So, if BC = 2k, then AB = k, is a positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2 = (2k)2 + (k)2
⇒ AC2 = 4k2 + k2 = 5k2
⇒ AC = √5k
Now, finding the other T-ratios using their definitions, we get:
sin θ = AB/AC = 5/√5k = 1/√2
cos θ = BC/AC = 2k/√5k = 2/√5
∴ tan θ = 1/cot θ = 1/2,
cosec θ = 1/sin θ = √5
sec θ = 1/cos θ = √5/2
5. If cosec θ = √10 find all the values of all T-ratios of θ
Solution
Let us first draw a right ∆ABC, right angled at B and ∠C = θ
Solution
We have sin θ = (a2 – b2)/(a2 + b2)
As,
Cos2 θ = 1 − sin2 θ
= 1 – (a2 – b2)/(a2 + b2)2
= 1/1 – (a2 – b2)2/(a2 + b2)2
= (a2 + b2)2 – (a2 – b2)2/(a2 + b2) + (a2 – b2)]/(a2 + b2)2
= [a2 + b2 – a2 + b2][a2 + b2 + a2 – b2]/(a2 + b2)2
= [2b2][2a2]/(a2 + b2)2
⇒ cos2 θ = 4a2b2/(a2 + b2)2
⇒ cos θ = 2ab/(a2 + b2)
Also,
tan θ = sin θ/cos θ
= [(a2 – b2)/(a2 + b2)]/[2ab/(a2 + b2)]
= (a2 – b2)/2ab
Now,
cosec θ = 1/sin θ
= 1/(a2 – b2)/(a2 – b2)
= (a2 + b2)/(a2 – b2)
Also,
sec θ = 1/cos θ
= 1/(2ab/(a2 + b2))
= (a2 + b2)/2ab
And,
cot θ = 1/tan θ
= 1/(a2 – b2)/2ab
= 2ab/(a2 – b2)
7. If 15 cot A = 8 find all the values of sin A and sec A
Solution
We have,
15 cot A = 8
⇒ cot A = 8/15
As,
cosec2 A = 1 + cot2 A
= 1 + (8/15)2
= 1 + 64/225
= (225 + 64)/225
⇒ cosec2A = 289/225
⇒ cosec A = 17/15
1/sin A = 17/15
Sin A = 15/17
Also,
Cos2 A = 1 – sin2 A
= 1 – (15/17)2
= 1 – 225/289
= (289 – 225)/289
⇒ cos2 A = 64/289
⇒ cos A = 8/17
⇒ 1/sec A = 8/17
⇒ sec A = 17/8
8. If sin A = 9/41 find all the values of cos A and tan A
Solution
We have sin A = 9/41
As,
Cos2 A = 1 − sin2 A
= 1 − (9/41)2
= 1 – 81/1681
= (1681 – 81)/1681
⇒ cos2 A = 1600/1681
⇒ cos A = 40/41
Also,
Tan A = sin A/cos A
= (9/41)/(40/41)
= 9/40
9. If cos θ = 0.6 show that (5sin θ - 3tan θ) = 0
Solution
Let us consider a right ∆ABC right angled at B.
Now, we know that cos θ = 0.6 = BC/AC = 3/5
So, if BC = 3k, then AC = 5k, where k is a positive number.
Using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ AB2 = AC2 – BC2
⇒ AB2 = (5k)2 – (3k)2 = 25k2 – 9k2
⇒ AB2 = 16k2
⇒ AB = 4k
Finding out the other T-rations using their definitions, we get:
Sin θ = AB/AC = 4k/5k = 4/5
tan θ = AB/BC = 4k/3k = 4/3
Substituting the values in the given expression, we get:
5 sin θ − 3 tan θ
⇒ 5(4/5) – 3(4/3)
⇒ 4 – 4 = 0 = RHS
i.e., LHS = RHS
Hence, Proved.
10. If cosec θ = 2 show that (cot θ + (sin θ/1 + cos θ) = 2
Solution
Let us consider a right ∆ABC, right angled at B and ∠C = θ.
Now, it is given that cosec θ = 2.
Also, sin θ = 1/cosec θ = 1/2 = AB/AC
So, if AB = k, then AC = 2k, where k is a positive number.
Using Pythagoras theorem, we have:
⇒ AC2 = AB2 + BC2
⇒ BC2 = AC2 – AB2
⇒ BC2 (2k)2 – (k)2
⇒ BC2 = 3k2
⇒ BC = √3k
Finding out the other T-ratios using their definitions, we get:
cos θ = BC/AC = √3k/2k = √3/2
tan θ = AB/BC = k/√3k = 1/√3
cot θ = 1/tan θ = √3
Substituting these values in the given expression, we get:
cot θ + sin θ/(1 + sin θ)
= (√3 + (1/2))/(1 + √3/2)
= (√3 + [(1/2)/(2 + √3)]/2
= √3 + 1/(2 + √3)
= (√3(2 + √3) + 1)/(2 + √3)
= (2√3 + 3 + 1)/(2 + √3)
= 2(2 + √3)/(2 + √3) = 2
i.e., LHS = RHS
Hence proved.
11. If tan θ = 1/√7 show that (cosec2 θ – sec2 θ)/(cosec2 θ + sec2 θ) = 3/4
Solution
Let us consider a right ∆ABC, right angled at B and ∠C = θ.
Now it is given that tan θ = AB/BC = 1/√7
So, if AB = k, then BC = √7k, where k is a positive number.
Using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ AC2 = (k)2 + (√7k)2
⇒ AC2 = k2 + 7k2
Now, finding out the values of the other trigonometric ratios, we have:
Sin θ = AB/AC = k/2√2k = 1/2√2
Cos θ = BC/AC = √7k/2√2k = √7/2√2
∴ cosec θ = 1/sin θ = 2√2 and sec θ = 1/cos θ = 2√2/√7
Substituting the values of cosec θ and sec θ in the give expression, we get:
(cosec2 θ – sec2 θ)/(cosec2 θ + sec2 θ)
= [(2√2)2 – (2√2)/√7)2]/[(2√2)2 + (2√2) /√7]2
= [8 – (8/7)]/[8 + (8/7)
= [(56 – 8)/7]/[56 + 8)/7]
= 48/64 = 3/4 = RHS
i.e., LHS = RHS
Hence proved.
12. If tan θ = 20/21, show that (1 – sin θ + cos θ)/(1 + sin θ + cos θ) = 3/7
Solution
Let us consider a right ∆ABC right angled at B and ∠C = θ
Now, we know that tan θ = AB/BC = 2θ/21
So, if AB = 20k, then BC = 21k, where k is a positive number.
Using Pythagoras theorem, we get:
AC2 = AB2 + BC2
⇒ AC2 = (20k)2 + (21k)2
⇒ AC2 = 841k2
⇒ AC = 29k
Now, sin θ = AB/AC = 20/29 and cos θ = BC/AC = 21/29
Substituting these values in the give expression, we get:
L.H.S = (1 - sin θ + cos θ)/(1 + sin θ + cos θ)
= [(1 – 20/29 + 21/29)]/[(1 + 20/29 + 21/29)]
= [(29 – 20 + 21|)/29]/[(29 + 20 + 21)/29
= 30/70
= 3/7 = R.H.S.
∴ LHS = RHS
Hence proved.
13. If sec θ = 5/4 show that (sin θ – 2 cos θ)/(tan θ – cot θ) = 12/7
Solution
We have,
Sec θ = 5/4
⇒ 1/cos θ = 5/4
⇒ cos θ = 4/5
Also,
sin2 θ = 1 – cos2 θ
= 1 – (4/5)2
= 1 – 16/25
= 9/25
⇒ sin θ = 3/5
Now,
L/H.S. = (sinθ – 2 cosθ)/(tanθ - cotθ)
= (sinθ – 2 cosθ)/(sin θ/cosθ – cosθ/sinθ)
= (sinθ – 2 cosθ)/(sin2θ – cos2θ)/(sinθ. cosθ)
= sinθ cosθ (sin θ – 2 cosθ)/(sin2θ – cos2θ)
= [3/5 × 4/5(3/5 – 2 × 4/5)]/[(3/5)2 – (4/5)2]
= 12/25(3/5 – 8/5)/(9/25 – 16/25)
= [12/25 × (-5/3)]/(-7)/25
= 12/7
= RHS
14. If cot θ = 3/4, show that = √(secθ-cosecθ)/(secθ+cosecθ= 1/√7
Solution
L.H.S. =
= 1/√715. If sin θ = 3/4, show that = √(cosec2θ-cot2θ)/(sec2θ-1) = √7/3
Solution
L.H.S. =
= √7/3
= RHS
16. If sin θ = a/b, show that (sec θ + tan θ) = √(b+a)/(b-a)
Solution
LHS = (sec θ + tan θ)
= 1/cos θ + sin θ/cos θ
= (1 + sin θ)/cos θ
= RHS
17. If cos θ = 3/5, show that (sin θ – cot θ)/ 2 tan θ = 3/160
Solution
L.H.S. = (sin θ – cot θ)/2 tan θ
= [sin θ – cos θ/sin θ]/[2(sin θ/cos θ)]
= [(sin2 θ – cos θ)/sin θ]/[(2 sin θ/cos θ)]
= [cos θ(sin2 θ – cos θ)/2 sin2 θ](2 sin2 θ]
= [cos θ(1 – cos2 θ – cos θ)]/[2(1 – cos2 θ)]
= 3/5[1 – (3/5)2 – 3/5]/2[1 – (3/5)2]
= [3/5(1/1 – 9/25 – 3/5)]/[2(1 – 9/25)]
= [3/5(25 – 9 – 15)/25]/[2(25 – 9)/25]
= [3/5(1/25)]/[2(16/25)]
= 3/(5 × 2 × 16)
= 3/160
= RHS
18. If tan θ = 4/3, show that (sin θ + cos θ) = 7/5
Solution
Let us consider a right ∆ABC, right angled at B and ∠C = θ
Now, we know that tan θ = AB/BC = 4/3
So, if BC = 3k, then AB = 4k, where k is a positive number.
Using Pythagoras theorem, we have:
AC2 = AB2 + BC2 = (4k)2 + (3k)2
⇒ AC2 = 16k2 + 9k2 = 25k2
⇒ AC = 5k
Finding out the values of sin θ and cos θ using their definitions, we have:
Sin θ = AB/AC = 4k/5k = 4/5
Cos θ = BC/AC = 3k/5k = 3/5
Substituting these values in the given expressions, we get:
(sin θ + cos θ) = (4/5 + 3/5) = (7/5) = RHS
i.e., LHS = RHS
Hence proved.
19. If tan θ = a/b, show that (a sin θ – b cos θ)/(a sin θ + b cos θ) = (a2 – b2)/(a2 + b2)
Solution
It is given that tan θ = a/b
LHS = (a sin θ – b cos θ)/(a sin θ + b cos θ)
Dividing the numerator and denominator by cos θ, we get:
(a tan θ – b)/(a tan θ + b) (∴ tan θ = sin θ/cos θ)
Now, substituting the value of tan θ in the above expression, we get:
[a(a/b) – b]/[a(a/b) + b]
= [a2/b – b]/[a2/b + b]
= (a2 – b2)/(a2 + b2)
= RHS
i.e., LHS = RHS
Hence proved.
20. If 3 tan θ = 4, show that (4 cos θ – sin θ)/(4 cos θ + sin θ) = 4/5
Solution
Let us consider a right ∆ABC right angled at B and ∠C = θ.
We know that tan θ = AB/BC = 4/3
So, if BC = 3k, then AB = 4k, where k is a positive number.
Using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ AC2 = 16k2 + 9k2
⇒ AC2 = 25k2
⇒ AC = 5k
Now, we have:
Sin θ = AB/AC = 4k/5k = 4/5
Cos θ = BC/AC = 3k/5k = 3/5
Substituting these values in the given expression we get:
(4 cos θ – sin θ)/(2 cos θ + sin θ)
= [4(3/5) – 4/5]/[2(3/5) + 4/5)]
= (12/5 + 4/5)/(6/5 + 4/5)
= [(12 – 4)/5]/[6 + 4)/5]
= 8/10
= 4/5
= RHS
i.e., LHS = RHS
Hence proved.
21. If 3cot θ = 2, show that (4 sin θ – 4 cos θ/0/(2 sin θ + 6 cos θ) = 1/3
Solution
It is given that cos θ = 2/3
LHS = (4 sin θ – 3 cos θ)/(2 sin θ + 6 cos θ)
Dividing the above expression by sin θ, we get:
(4 – 3 cos θ)/(2 + 6 cot θ) [∵ cot θ = cos θ/cot θ]
Now, substituting the values of cot θ in the above expression, we get:
= [4 – 3(2/3)]/[2 + 6(2/3)]
= (4 – 2)/(2 + 4)
= 2/6
= 1/3
i.e., LHS = RHS
Hence proved.
22. If 3 cot θ = 4 show that (1 – tan2 θ)/(1 + tan2 θ) = (cos2 θ – sin2 θ)
Solution
LHS = (1 – tan2 θ)(1 + tan2 θ)
= (1 – 1/cot2 θ)/(1 + 1/cot2 θ)
= [(cot2 θ – 1)/cot2 θ]/[(cot2 θ + 1)/cot2 θ]
= (cot2 θ – 1)/(cot2 θ + 1)
= [(4/3)2 – 1]/[(4/3)2 + 1] (As 3 cot θ = 4 or cot θ = 4/3)
= (16/9 – 1)/(16/9 + 1)
= [(16 – 9)/9]/[(16 + 9)/9]
= (7/9)/(25/9)
= 7/25
RHS = (cos2 θ – sin2 θ)
= (cos2 θ – sin2 θ)/1
= [(cos2 θ – sin2 θ)/sin2 θ]/(1/sin2 θ)
= [cos2 θ/sin2 θ – sin2 θ/sin2 θ]/cosec2 θ
= (cot2 θ – 1)/(cot2 θ + 1)
= [(4/3)2 – 1]/[(4/3)2 + 1]
= (16/9 – 1/1)/(16/9 + 1/1)
= (16 – 9)/9/(16 + 9)/9
= (7/9)/(25/9)
= 7/25
Since, LHS = RHS
Hence, verified.
23. If sec θ = 17/8 verify that (3 – 4 sin2 θ)/(4 cos2 θ – 3) = (3 – tan2 θ)/(1 – tan3 θ)
Solution
It is given that sec θ = 17/8
Let us consider a right ∆ABC right angled at B and ∠C = θ
We know that cos θ = 1/sec θ = 8/17 = BC/AC
So, if BC = 8k, then AC = 17k, where k is a positive number.
Using Pythagoras theorem, we have:
AC2 = AB2 + BC2
⇒ AB2 = AC2 – BC2 = (17k)2 – (8k)2
⇒ AB2 = 289k2 – 64k2 = 225k2
⇒ AB = 15k.
Now, tan θ = AB/BC = 15/8 and sin θ = AB/AC = 15k/17k = 15/17
The given expression is (3 – 4 sin2 θ)/(4 cos2 θ – 3) = (3 – tan2 θ)/(1 – 3 tan2 θ)
Substituting the values in the above expression, we get:
LHS = [3 – 4(15/17)2]/[4(8/17)2 – 3]
= (3 – 900/289)/(256/289 – 3)
= (867 – 900)/(256 – 867)
= -(33/-611)
= 33/611
RHS = [3 – (15/8)2]/[(1 – 3(15/8)2]
= [3 – 225/64]/[1 – 675/64]
= (192 – 255)/(64 – 675)
= - (33/-611) = 33/611
∴ LHS = RHS
Hence proved.
24. In the adjoining figure, ∠B = 90°, ∠BAC = θ°, BC = CD = 4 cm and AD = 10 cm. find (i) sin θ and (ii) cos θ
SolutionIn ∆ABD,Using Pythagoras theorem, we get
Again,
In ∆ABC,
Using Pythagoras theorem, we get
Now,
(i) sin θ = BC/AC
(ii) cos θ = AB/AC
AC2 = AB2 + BC2
⇒ AC2 = (24)2 + (7)2
⇒ AC2 = 576 + 49 = 625
⇒ AC = 25 cm
Now, for T-Ratios of ∠A, base = AB and perpendicular = BC
(i) sin A = BC/AC = 7/25
(ii) cos A = AB/AC = 24/25
Similarly, for T-Ratios of ∠C, base = BC and perpendicular = AB
(iii) sin C = AB/AC = 24/25
(iv) cos C = BC/AC = 7/25
26. In ΔABC, ∠C = 90°, ∠ABC = θ° BC = 21 units and AB = 29 units. Show that (cos2 θ – sin2 θ) = 41/841
Solution
Using Pythagoras theorem, we get:AB2 = AC2 + BC2
⇒ AC2 = AB2 – BC2
⇒ AC2 = (29)2 – (21)2
⇒ AC2 = 841 – 441
⇒ AC2 = 400
= 20 units
Now, sin θ = AC/AB = 2θ/29 and cos θ = BC/AB = 21/29
cos2 θ – sin2 θ = (21/29)2 – (20/29)2
= 441/841 – 400/841
= 41/841
Hence proved.
27. In a ΔABC, ∠B = 90°, AB = 12 cm and BC = 5 cm Find (i) cos A (ii) cosec A (iii) cos C (iv) cosec C
Solution
AC2 = AB2 + BC2
Now, for T-Ratios of ∠A, base = AB and perpendicular BC
(i) cos A = AB/AC = 12/13
(ii) cosec A = 1/sin A = AC/BC = 13/5
Similarly, for T-Ratios of ∠C, base = BC and perpendicular = AB
(ii) cos C = BC/AC = 5/13
(iv) cosec C = 1/sin C = AC/AB = 13/12
28. If sin α = 1/2 prove that (3 cos α – 4 cos2 α) = 0
Solution
LHS = (3cos α − 4 cos3 α)
= cos α (3 − 4 cos2 α)
= 0
= RHS
29. If ΔABC, ∠B = 90° ABD Tan A = 1/√3. Prove that
(i) Sin A. cos C + cos A. Sin c = 1
(ii) cos A. cos C - sin A. sin C = 0
Solution
In ∆ABC, ∠B = 900,As, tan A = 1/√3
⇒ BC/AB = 1/√3
Let BC = x and AB = x√3
Using Pythagoras we get
Now,
(i) LHS = sin A. cos C + cos A. sin C
= (BC/AC)2 + (AB/AC)2
= (x/2x)2 + (x√3/2x)2
= 1/4 + 3/4
= 1
= RHS
(ii) LHS = cos A. cos C – sin A. sin C
= AB/AC.BC/AC – BC/AC.AB/AC
= (x√3/2x.x/2x) – (x/2x.x√3/2x)
= √3/4 - √3/4
= 0
= RHS
30. If √A and √B are acute angles such that Sin A = Sin B prove that ∠A = ∠B
Solution
In ∆ABC, √C = 90°Sin A = BC/AB and
Sin B = AC/AB
As, sin A = sin B
⇒ BC/AB = AC/AB
⇒ BC = AC
So, ∠A = ∠B (Angles opposite to equal sides are equal)
31. If ∠A and ∠B are acute angles such that tan A = Tan B then prove that ∠A = ∠B
Solution
In ∆ABC, ∠C = 900Tan A = BC/AC and
Tan B = AC/BC
As tan A = tan B
⇒ BC/AC = AC/BC
⇒ BC2 = AC2
⇒ BC = AC
So, ∠A = ∠B (Angles opposite to equal sides are equal)
32. If a right ΔABC, right-angled at B, if tan A = 1 then verify that 2sin A. cos A = 1
Solution
We have,
Tan A = 1
⇒ sin A/cos A = 1
⇒ sin A = cos A
⇒ sin A – cos A = 0
Squaring both sides,
(sin A – cos A)2 = 0
⇒ sin2 A + cos2 A – 2 sin A. cos A = 0
⇒ 1 – 2 sin A. cos A = 0
∴ 2 sin A. cos A = 1
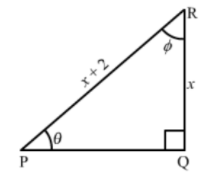
33. In the figure of ΔPQR, ∠P = θ° P θ and ∠R = φ° find
(i) √(x+1) cotɸ
(ii) √(x3 +x2) cotɸ
(iii) cos θ
SolutionIn ∆PQR, ∠Q = 900,Using Pythagoras theorem, we get
Now,
(i)
(ii)
(iii) cos θ
Solution
LHS = (2/x + y)2 + (x – y/2)2 – 1
= [2/(cosec A + cos A) + (cosec A – cos A)]2 + [(cosec A + cos A) – (cosec A – cos A)/2]2 – 1
= [2/(cosec A + cos A + cosec A – cos A]2 + [cosec A + cos A – cosec A + cos A/2]2 – 1
= [2/2 cosec A]2 + [2 cos A/2]2 – 1
= [1/cosec A]2 + [cos A]2 – 1
= [sin A]2 + [cos A]2 – 1
= sin2 A + cos2 A - 1
= 1 - 1
= RHS
35. If x = cot A + cos A and y = cot A – cos A then prove that [(x – y)/(x + y)]2 + (x – y/2)2 = 1
Solution
LHS = (x – y/x + y)2 + (x – y/2)2
= [(cot A + cos A – cot A – cos A)/(cot A + cos A + cot A – cos A) + [(cot A + cos A – cot A + cos A)/2]2
= [2cos A/2cot A]2 + [2cos A/2]2
= [cos A/(cos A/sin A)]2 + [cos A]2
= [sin A cos A/cos A]2 + [cos A]2
= sin2 A + cos2 A
= 1
= RHS