RS Aggarwal Solutions Chapter 3 Linear Equations in Two Variables Exercise - 3C Class 10 Maths
Chapter Name | RS Aggarwal Chapter 3 Linear Equations in Two Variables |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 3C Solutions
1. Solve the system of equations by using the method of cross multiplication: x + 2y + 1 = 0,
2x – 3y – 12 = 0.
Solution
The given equations are:
x + 2y + 1 = 0 ….(i)
2x – 3y – 12 = 0 ….(ii)
Here a1 = 1, b1 = 2, c1 = 1, a2 = 2, b2 = -3 and c2 = -12
By cross multiplication, we have:
∴ x[2×(−12) −1×(−3)] = y/[1×2 − 1×(−12)] = 1/[1×(−3) − 2×2]
⇒ x/(-24 + 3) = y/(2 + 12) = 1/(-3 - 4)
⇒ x/(-21) = y/14 = 1/(-7)
⇒ x = - 21/-7 = 3, y = 14/-7 = -2
Hence, x = 3 and y = -2 is the required solution.
2. Solve the system of equations by using the method of cross multiplication:
3x - 2y + 3 = 0,
4x + 3y – 47 = 0
Solution
The given equations are:
3x - 2y + 3 = 0 ….(i)
4x + 3y – 47 = 0 ….(ii)
Here a1 = 3, b1 = -2, c1 = 3, a2 = 4, b2 = 3 and c2 = -47
By cross multiplication, we have:
∴ x/[(−2)×(−47) − 3×3] = y/[3×4 − (−47) × 3] = 1/[3×3 − (−2) × 4]
⇒ x/(94 – 9) = y/(12 + 141) = 1/(9 + 8)
⇒ x/(85) = y/(153) = 1/(17)
⇒ x = 85/17 = 5, y = 153/17 = 9
Hence, x = 5 and y = 9 is the required solution.
3. Solve the system of equations by using the method of cross multiplication:
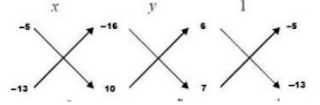
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solution
The given equations are:
6x - 5y - 16 = 0 ….(i)
7x - 13y + 10 = 0 ….(ii)
Here a1 = 6, b1 = -5, c1 = -16, a2 = 7, b2 = -13 and c2 = 10
By cross multiplication, we have:
∴ x/[(−5)×10 −(−16)×(−13)] = y/[(−16)×7 −10×6] = 1/[6×(−13)−(−5)×7]
⇒ x/(-50 – 208) = y/(-112 – 60) = 1/(-78 + 35)
⇒ x/(-258) = y/(-172) = 1/(43)
⇒ x = (-258/-43) = 6, y = - 172/-43 = 4
Hence, x = 6 and y = 4 is the required solution.
4. Solve the system of equations by using the method of cross multiplication:
3x + 2y + 25 = 0, 2x + y + 10 = 0
Solution
The given equations are:
3x + 2y + 25 = 0 ….(i)
2x + y + 10 = 0 ….(ii)
Here a1 = 3, b1 = 2, c1 = 25, a2 = 2, b2 = 1 and c2 = 10
By cross multiplication, we have:
∴ x/[2×10 −25×1] = y/[25×2 −10×3] = 1/[3×1 − 2×2]
⇒ x/(20 – 25) = y/(50 – 30) = 1/(3 – 4)
⇒ x/(-5) = y/20 = 1/(-1)
⇒ x = -5/-1 = 5, y = 20/(-1) = - 20
Hence, x = 5 and y = -20 is the required solution.
5. Solve the system of equations by using the method of cross multiplication:
2x + 5y – 1 = 0, 2x + 3y – 3 = 0
Solution
The given equations may be written as:
2x + 5y – 1 = 0 ….(i)
2x + 3y – 3 = 0 ….(ii)
Here a1 = 2, b1 = 5, c1 = -1, a2 = 2, b2 = 3 and c2 = -3
By cross multiplication, we have:
∴ x/[5 × (−3) −3 × (−1)] = y/[(−1) × 2 −(−3) × 2] = 1/[2 × 3−2 × 5]
⇒ x/(-15 + 3) = y/(-2 + 6) = 1/(6 – 10)
⇒ x/-12 = y/4 = 1/-4
⇒ x = -12/-4 = 3, y = 4/-4 = -1
Hence, x = 3 and y = -1 is the required solution.
6. Solve the system of equations by using the method of cross multiplication:
2x + y – 35 = 0,
3x + 4y – 65 = 0
Solution
The given equations may be written as:
2x + y – 35 = 0 ...(i)
3x + 4y – 65 = 0 ….(ii)
Here a1 = 2, b1 = 1, c1 = -35, a2 = 3, b2 = 4 and c2 = -65
By cross multiplication, we have:
⇒ x/(-65 + 140) = y/(-105 + 130) = 1/(8 – 3)
⇒ x/75 = y/25 = 1/5
⇒ x = 75/5 = 15, y = 25/5 = 5
Hence, x = 15 and y = 5 is the required solution.
7. Solve the system of equations by using the method of cross multiplication:
7x - 2y – 3 = 0,
11x - 3/2y – 8 = 0.
Solution
The given equations may be written as:
7x - 2y – 3 = 0 ….(i)
11x - 3/2y – 8 = 0 ….(ii)
Here a1 = 7, b1 = -2, c1 = -3, a2 = 11, b2 = -(3/2) and c2 = -8
By cross multiplication, we have:
∴ x/[(−2) × (−8) – (-3/2) × (-3)] = y/[(−3) × 11 −(−8) × 7] = 1/[7 × (-3/2) − 11 × (−2)]
⇒ x/(16 – 9/2) = y/(-33 + 56) = 1/(-21/2 + 22)
⇒ x/(23/2) = y/23 = 1/(23/2)
⇒ x = (23/2)/(23/2) = 1, y = 23/(23/2)
Hence, x = 1 and y = 2 is the required solution.
8. Solve the system of equations by using the method of cross multiplication:
x/6 + y/15 – 4 = 0, x/3 – y/12 – 19/4 = 0
Solution
The given equations may be written as:
x/6 + y/15 – 4 ….(i)
x/3 – y/12 – 19/4 = 0 ….(ii)
Here a1 = 1/6, b1 = 1/15, c1 = -4, a2 = 1/3, b2 = -1/12 and c2 = -19/4
By cross multiplication, we have:
∴ x/(1/15 ×(−19/4) − (−1/12)×(−4)] = y/[(−4)× 1/3 − (1/6)×(−19/4)] = 1/[1/6 × (−1/12) × 1/3 × 1/15]
⇒ x/(-19/60 – 1/3) = y/(-4/3 + 19/34) = 1/(-1/72 – 1/45)
⇒ x = [-(39/60) × -(360/13)] = 18, y = [(−13/24) × (−360/13)] = 15
Hence, x = 18 and y = 15 is the required solution.
9. Solve the system of equations by using the method of cross multiplication:
Solution
Taking 1/x = u and 1/y = v, the given equations become:
u + v = 7
2u + 3v = 17
The given equations may be written as:
u + v – 7 = 0 ...(i)
2u + 3v – 17 = 0 …(ii)
Here, a1 = 1, b1 = 1, c1 = -7, a2 = 2, b2 = 3 and c2 = -17
By cross multiplication, we have:
∴ u/[1 × (−17) −3 × (−7)] = v/[(−7) × 2 −1 × (−17)] = 1/[3 − 2]
⇒ u/(-17 + 21) = v/(-14 + 17) = 1/(1)
⇒ u/4 = v/3 = 1/1
⇒ u = 4/1 = 4, v = 3/1 = 3
⇒ 1/x = 4, 1/y = 3
⇒ x = 1/4, y = 1/3
Hence, x = 1/4 and y = 1/3 is the required solution.
10. Solve the system of equations by using the method of cross multiplication:
5/(x + y) – 2/(x – y) + 1 = 0, 15/(x + y) + 7/(x – y) – 10 = 0
Solution
Taking 1/(x + y) = u and 1/(x – y) = v, the given equations become:
5u - 2v + 1 = 0 ...(i)
15u + 7v – 10 = 0 …(ii)
Here, a1 = 5, b1 = -2, c1 = 1, a2 = 15, b2 = -7 and c2 = -10
By cross multiplication, we have:
∴ u/[−2 × (−10) −1 × 7] = v/[1 × 15 −(−10) × 5] = 1/[35 + 30]
⇒ u/(20 – 7) = v/(15 + 50) = 1/65
⇒ u/13 = v/65 = 1/65
⇒ u = 13/65 = 1/5, v = 65/65 = 1
⇒ 1/(x + y) = 1/5, 1/(x – y) = 1
So, (x + y) = 5 ...(iii)
and (x – y) = 1 …(iv)
Again, the above equations (ii) and (iv) may be written as:
x + y – 5 = 0 ...(i)
x – y – 1 = 0 …(ii)
Here, a1 = 1, b1 = 1, c1 = -5, a2 = 1, b2 = -1 and c2 = -1
By cross multiplication, we have:
∴ x/[1 × (−1) −(−5) × (−1)] = y/[(−5) × 1 −(−1) × 1] = 1 = 1/[1 × (−1) −1 × 1]
⇒ x/(-1 – 5) = y/(-5 + 1) = 1/(-1 – 1)
⇒ x/-6 = v/-4 = 1/-2
⇒ x = −6/-2 = 3, y = −4/-2 = 2
Hence, x = 3 and y = 2 is the required solution.
11. Solve the system of equations by using the method of cross multiplication:
ax/b – by/a – (a + b) = 0, ax – by – 2ab = 0
Solution
The given equations may be written as:
ax/b – by/a – (a + b) = 0 …(i)
ax – by – 2ab = 0 …(ii)
Here, a1 = a/b, b1 = -b/1, c1 = -(a + b), a2 = a, b2 = -b and c2 = -2ab
By cross multiplication, we have:
∴ x/[(−b/a) × (−2ab) −(-b) × (−(a + b)] = y/[−(a + b) × a −(−2ab) ×a/b] = 1/[a/b × (−b) × (−b/a)]
⇒ x/[2b2 – b(a + b)] = y/[-a(a + b) + 2a2] = 1/(-a + b)
⇒ x/(b2 – ab – b2) = y/(-a2 – ab + 2a2) = 1/(-a + b)
⇒ x/(b2 – ab) = y/(a2 – ab) = 1/-(a – b)
⇒ x/(-b(a – b) = y/a(a – b) = 1/-(a – b)
⇒ x = -b(a – b)/-(a – b) = b, y = a(a – b)/(-a – b) = - a
Hence, x = b and y = -a is the required solution.
12. Solve the system of equations by using the method of cross multiplication:
2ax + 3by – (a + 2b) = 0,
3ax + 2by – (2a + b) = 0
Solution
The given equations may be written as:
2ax + 3by – (a + 2b) = 0 …(i)
3ax + 2by – (2a + b) = 0 …(ii)
Here, a1 =2a, b1 =3b, c1 = -(a + 2b), a2 = 3a, b2 = 2b and c2 = -(2a + b)
By cross multiplication, we have:
∴ x[3b × (-2a + b) -2b × (-(a + 2b))] = y/[-a + 2b) × 3a – 2a × (-2a + b)] = 1/[2a × 2b -3a × 3b]
⇒ x/(-6ab – 3b2 + 2ab + 4b2) = y/(-3a2 – 6ab + 4a2 + 2ab) = 1/(4ab – 9ab)
⇒ x/(b2 – 4ab) = y/(a2 – 4ab) = 1/-5ab
⇒ x/(-b(4a – b) = y/-a(4b – a) = 1/-5ab
⇒ x = -b(4a – b)/-5ab = (4a – b)/5a, y = -a(4b – a)/-5ab = (4b – a)/5b
Hence, x = (4a – b)/5a and y = (4b – a)/5b is the required solution.
13. Solve the system of equations by using the method of cross multiplication:
a/x – b/y = 0, ab2/x + a2b/y = (a2 + b2), where x ≠ 0 and y ≠ 0
Solution
Substituting 1/x = u and 1/y = v in the given equations, we get
au – bv + 0 = 0 ….(i)
ab2u + a2bv – (a2 + b2) = 0 …(ii)
Here, a1 = a, b1 = -b, c1 = 0, a2 = ab2, b2 = a2b and c2 = -(a2 + b2).
So, by cross-multiplication, we have
u/(b1c2 – b2c1) = v/(c1a2 – c1a2) = 1/(a1b2 – a2b1)
⇒ u/(-b)[-(a2 + b2)] – (a2b)(0) = v/(0)(ab2)-(-a2 – b2)(a) = 1/(a)(a2b)-(ab2)(-b)
⇒ u/b(a2 + b2) = v/a(a2 + b2) = 1/ab(a2 + b2)
⇒ u = b(a2 + b2)/ab(a2 + b2), v = a(a2 + b2)/ab(a2 + b2)
⇒ u = 1/a, v = 1/b
⇒ x = a, y = b
Hence, x = a and y = b.