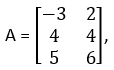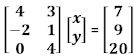Revision Notes for Matrices Class 10 Maths ICSE

ICSE Revision Notes for Matrices Class 10 Maths

Chapter Name	Matrices
Topics Covered	Matrix and its Various Types  Transpose of a Matrix and Related Properties  Equality of Matrices Addition and Subtraction of Matrices  Multiplication of a Matrix by a Scalar and Related Properties
Related Study	Selina Maths ICSE Solutions for Class 10 ML Aggarwal Solutions for Class 10 Maths Frank ICSE Solutions for Class 10 Maths

Matrix and its Various Types 

Matrices and their Related Terminology 

A matrix is an ordered rectangular array of numbers and functions. The numbers or functions in a matrix are called the elements of the matrix.

For example, if the marks obtained by Smita in English, Maths and Science are 84, 93, and 89 respectively and the marks scored by Gopal are 81, 90, and 92 respectively, then this can be represented in the form of matrix asor as 

Here, in the first matrix, the vertical lines of elements represent the marks obtained by Smita and Gopal respectively. In the second matrix, the horizontal lines of elements represent the marks obtained by Smita and Gopal.

The matrices are usually denoted by capital letters. The horizontal line of elements is known as the row of matrix and the vertical line of elements is known as the column of matrix. 

A matrix with m rows and n columns is known as the matrix of order m × n or an m × n matrix.

For example: is a 3 × 2 matrix and is a 2 × 3 matrix. 

In general, an m × n matrix represents the matrix

It can also be represented as A = [a_ij]_m×n, 1 ≤ i ≤ m, 1 ≤ j ≤ n; i, j ∈ N. . 

This means that the i^th row has elements a_i1, a_i2 … a_ij … a_in and the j^th column has elements a_1j, a_2j… a_ij … a_mj. 

An m × n matrix has mn number of elements.

Types of Matrices

A matrix is said to be a column matrix if it has only one column.

For example: 

is a column matrix. 

A matrix is said to be a row matrix if it has only one row.

For example:is a row matrix.

A matrix in which the number of rows is equal to the number of columns is called a square matrix. In a square matrix, m = n. Therefore, it is known as a square matrix of order n. It is represented by A = [a_ij]_m×n

For example:

is a square matrix of order 3.

A matrix is said to be a rectangular matrix if the number of rows is not equal to the number of columns.

For example:

is a rectangular matrix. 

In a square matrix A = [a_ij]_n×n , the elements a₁₁, a₂₂ … a_nn are called the diagonal elements of A = [a _ij]_n×n. For instance, for the square matrix , the diagonal elements are 3, 4, and 8. If all the non-diagonal elements of a square matrix are zero, then the square matrix is known as a diagonal matrix i.e., a square matrix A = [a_ij ]_n×n is a diagonal matrix if a_ij = 0, whenever i ≠ j.

For example:

, are diagonal matrices. 

A diagonal matrix in which all the diagonal elements are equal is known as a scalar matrix i.e., square matrix A = [a_ij ]_n×n is a scalar matrix if

a_ij = 0, when i ≠ j 

a_ij = k, when i = j, where k is a constant. 

For example:

, are scalar matrices. 

A square matrix in which all the diagonal elements are 1 and all other elements are zero is known as an identity matrix i.e., A = [a_ij]_n×n is an identity matrix if 

a_ij = 1, when i = j 

a_ij = 0, when i ≠ j

For example:

are identity matrices of order 2 and 3 respectively.

A matrix is known as a zero or null matrix if all its elements are zero.

For example:, are all zero matrices. 

Let us solve some examples on matrices. 

Example 1: The lengths of the sides of two triangles are 2 cm, 5 cm, 8 cm and 3 cm, 4 cm, 5 cm.  Represent this in the form of a 2 × 3 matrix. 

Answer

A 2 × 3 matrix is represented as

The lengths of sides can be represented in the form of matrix as

Here, the first row represents the sides of the first triangle and the second row represents the sides of the second triangle. 

Example 2: Construct a square matrix of order 3 whose elements are given by a_ij = 1/2 |2i – j|.

Answer

A 3 × 3 matrix is represented as 

a₁₁ = 1/2|2.1 – 1| = ½, a₁₂ = 1/2|2.1 – 2| = 0, a₁₃ = ½|2.1 – 3| = ½ |-1| = 1/2

a₂₁ = 1/2|2.2 – 1| = 3/2, a₂₂ = ½|2.2 – 2| = 1, a₂₃ = 1/2|2.2 – 3|= 1/2

a₃₁ = 1/2|2.3 – 1| = 5/2. a₃₂ = 1/2|2.3 -2| = 2, a₃₁ = 1/2|2.3 – 3| = 3/2

Thus, the required matrix is

Transpose of a Matrix and Related Properties 

Transpose of a Matrix

If A = [a_ij]_m×n is a matrix of order m × n, then the matrix obtained by interchanging its rows and columns is known as the transpose of A.

It is denoted by A' . In general, if  A = [a_ij]_m×n, then A' = [a_ij]_m×n

For example:

If, then 

Properties of Transpose of Matrix

If A and B are two matrices, then 

(A’)’ = A

(KA´)´ = KA, where K is a constant

(A + B)' = A' + B'

(AB)' = B'A'

Note: Transpose of a row matrix is a column matrix and vice versa. 

For example, 

Solved Examples 

Example 1:

If, then prove that (A + B)' = A' + B' 

Answer

From (1) and (2), we obtain 

(A + B)' = A' + B' 

Thus, given result is proved. 

Example 2: If  then prove that (AB)' = B'A'

Answer

From (1) and (2), we obtain (AB)' = B'A'.

Thus, the given result is proved. 

Example 3: If then determine the transpose of A. 

Answer

The transpose of A is given by

Example 4: Let m × n be the order a matrix A. If the order of the transpose of the matrix A is 4 × 3 then find the value of m and n.

Answer

Order of the matrix A = m × n

Order of transpose of the matrix A = n × m = 4 × 3 

Therefore, n = 4 and m = 3. 

Example 5: Let A =, then show that (A')' + A =

Answer

Here, 

Equality of Matrices

Two matrices A = [a_ij] and B = [b_ij] and are said to be equal (denoted as A = B) if they are of the sameorder and each element of A is equal to the corresponding element of B i.e., a_ij = b_ij for all i and j.

For example:

 are equal butare not equal

Solved Examples 

Example 1: If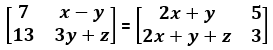, then find the values of x, y and z.

Answer

Since the corresponding elements of equal matrices are equal, 

2x + y = 7…(1) 

x − y = 5…(2) 

2x + y + z = 13…(3) 

3y + z = 3…(4) 

On solving equations (1) and (2), we obtain x = 4 and y = −1. 

On substituting the value of y in equation (4), we obtain z = 6. 

Thus, the values of x, y and z are 4, −1 and 6 respectively. 

Example 2: Ifare two equal matrices, then find matrix A and matrix B. 

Answer

The given matrices are equal. Therefore, their corresponding elements are equal. On comparing the corresponding elements, we obtain 

a + b = −a 

⇒ 2a + b = 0…(1)

2b − c = 3c 

⇒ 4c − 2b = 0…(2) 

b = −b + a + 5 

⇒ −a + 2b = 5…(3) 

On solving equations (1) and (3), we obtain a = −1 and b = 2. 

On substituting the value of b in equation (2), we obtain c = 1. 

In matrix A, 

a₁₁ = a + b = −1 + 2 = 1 

a₁₂ = 2b − c = 2(2) − 1 = 3 

a₂₂ = b = 2 

Since A and B are equal matrices, B is the same as matrix A. 

Thus, matrix A and matrix B are 

Addition and Subtraction of Matrices 

Addition of Matrices and its Properties 

The sum of two matrices is obtained by adding their corresponding elements. Two matrices can be added only if their orders are same. 

In general, if A = [a_ij] and B = [b_ij] and are two matrices of order m × n, then the sum of these matrices is given by C = [c _ij]_m×n, where c_ij = a_ij + b_ij. 

For example: 

The sum of matrices whose order is not the same is not defined. 

If A = [a_ij], B = [b_ij], C = [c_ij] are three matrices of the same order, then their addition satisfies the following properties: 

The addition of matrices is commutative i.e., A + B = B + A 

The addition of matrices is associative i.e., (A + B) + C = A + (B + C) 

For every matrix A, there exists a zero matrix O of the same order such that A + O = O + A = A. O is the additive identity of the matrix addition. 

For every matrix A, there exists another matrix −A of same order such that A + (−A) = (−A) + A = O. (−A) is the additive inverse of A.

Subtraction of Matrices

The difference of two matrices A = [a_ij] and B = [b_ij] of the same order m × n, (say B from A) is given by, where c_ij = a_ij − b_ij. 

For example: 

The difference of matrices whose orders are not the same is not defined. 

• A − B  ≠ B − A

Solved Examples 

Example 1:

If , then find the values of x and y. 

Answer

According to the given information, 

On equating the corresponding elements, we obtain

x – 4y = - 3 ...(1)

2x + 3y = 5 ....(2)

On equating (1) and (2), we obtain x = 1 and y = 1

Thus, the values of x and y are 1 and 1 respectively.

Example 2:

If 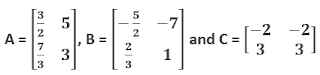 are three matrices, then prove that A + B - C is an identity matrix. 

Answer

Thus,  A + B - C is an identity matrix. 

Multiplication of a Matrix by a Scalar and Related Properties 

Multiplication of a Matrix by a Scalar

A matrix A, when multiplied by a scalar k, gives another matrix kA, which is obtained by multiplying each element of matrix A by the scalar k. In general, if A = [a_ij]_m×n, then kA = k[a_ij]_m×n = [k(a_ij)]_m×n i.e., (i, j)^th , element of kA is ka_ij, for all values of i and j. 

For example:

If then 3A is given by

The negative of a matrix is obtained by multiplying the matrix with −1 i.e., if A is a matrix, then its negative is (−1)A = −A. 

If A = [a_ij] and B = [b_ij] are two matrices of the same order i.e., m × n, and k and l are scalars, then A and B satisfies the following properties: 

k (A + B) = kA + kB

(k + l) A = kA + lA

Solved Examples 

Example 1:

Find the value of 2A − 3B, where

Answer

Example 2: 

If , then find the values of a and b. 

Answer

On equating the corresponding elements, we obtain 

−6 − 5a = −1 

⇒ a = −1 

9 − 5b = −1 

⇒ b = 2 

Thus, the values of a and b are −1 and 2 respectively. 

Multiplication of Matrices and Related Properties 

Multiplication of Matrices 

The product of two matrices A and B is defined only if the number of columns of A is equal to the number of rows of B i.e., if A = [a_ij ]_m×n and B = [b_jk]_n×p, only then AB is defined. 

If A is a matrix of order m×n and B is a matrix of order n×p, then their product, say, C = AB, is of the order m×p. To find the (i, k)^th element, (c_ik) of matrix C (= AB), multiply the elements of the i^th row of A and the elements of the k^th column of B and take the sum of all their products. 

If the product of two matrices is a zero matrix, then it is not necessary that one of the matrices is a zero matrix.

Properties of Multiplication of Matrices 

The multiplication of three matrices A, B and C satisfies the following properties: 

The multiplication of matrices is non-commutative i.e., the product AB and BA may or may not be equal.

For example:

If 

The multiplication of diagonal matrices of the same order is commutative. 

The multiplication of matrices is associative i.e., (AB)C = A (BC).

Distributive law is satisfied for any three matrices. 

A(B + C) = AB + AC

(A + B)C = AC + BC 

For every square matrix A, there exists an identity matrix I of the same order such that AI = IA = A.

Solved Examples 

Example 1:

 If , then what are the values of x and y? 

Answer

∴ 4x + 3y = 7 ...(1)

− 2x + y = 9 ...(2)

4y = 20 ...(3)

From equation (3), we obtain y = 5. 

On substituting this value in equation (2), we obtain x = −2. 

Thus, the values of x and y are −2 and 5 respectively.

Example 2:

If A = , then prove that A(B + C) = AB + BC. 

Answer

From (1) and (2), we obtain

A(B + C) = AB + AC

Thus, the result is proved.