ICSE Revision Notes for Linear Inequation Class 10 Maths
Chapter Name | Linear Inequations |
Topics Covered |
|
Related Study |
Inequality and its Classification
Two real numbers or two algebraic expressions related by the symbols ‘<’, ‘>’, ‘≤’ or ‘≥’ form an inequality.
For example: 6 < 26, 3 < z + 1 ≤ 22, 27 ≥ s ≥ 16, p + t > 100
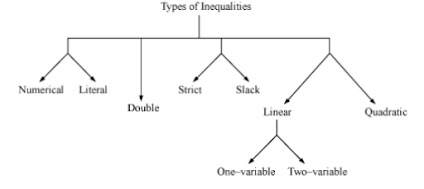
Inequalities can be classified as
Numerical inequality: Inequalities that involve numbers only are classified as numerical inequalities. For example: 87 < 117, 19 > 17 > 8 etc.
Literal inequality: Inequalities that involve a variable on one side and a number on the other side are classified as literal inequalities. For example: a < 6, 18 > k, b ≥ − 27, 21 ≤ m, etc.
Double inequality: Inequalities in which the variable or the numbers lie in a certain interval are known as double inequalities. For example: x ∈ [−15, 8], 9 > 6 > 2, 8 ≤ p + 1 ≤ 11, etc.
Strict inequality: Inequalities of the type px + q < 0, px + q > 0, px + qy < r, px + qy > r, ax2 + bx + c > 0, or ax2 + bx + c < 0 are classified as strict inequalities. For example: 2x < − 3, x + 17 < 9, x + 3y > 14, 2a + 5b < 8, 2y2 + 5y > 8 etc.
Slack inequality: Inequalities of the type px + q ≤ 0, px + q ≥ 0, px + qy ≤ r, px + qy ≥ r, ax2 + bx + c ≥ 0, or ax2 + bx + c ≤ 0 are classified as slack inequalities. For example: x ≤ 89, 5x + 8y ≤ 9, 8x + y ≥ 7, x + 14 ≥ 28, z2 + 3z ≤ 30 etc.
- Linear inequality in one variable: Inequalities of the type px + q ≥ 0, px + q ≤ 0, px + q > 0, or px + q < 0, where p ≠ 0, are classified as linear inequalities in one variable (here, the variable in each inequality is x). For example: x − 23 ≥ 0, 12y < 85, etc.
- Linear inequality in two variables: Inequalities of the type px + qy + r ≥ 0, px + qy + r ≤ 0, px + qy + r > 0, or px + qy + r < 0, where p ≠ 0 and q ≠ 0, are classified as linear inequalities in two variables (here, the variables in each inequality are x and y). For example: 9x + y > 0, x + 11y ≥ 13, etc.
- Quadratic inequality: Inequalities of the type ax2 + bx + c ≥ 0, ax2 + bx + c ≤ 0, ax2 + bx + c > 0, or ax2 + bx + c < 0, where a ≠ 0, are classified as quadratic inequalities. For example: x2 + 16 ≥ 23, p2 < 2p + 7, etc.
Let's now try and solve the following puzzle to check whether we have understood this concept.
Let us now solve an example based on inequality.
Example 1: State true or false for the following statements:
1. The inequality 9x2 + 5x < 0 is a quadratic inequality.
2. The inequality 7p + 3q > 2 is a linear inequality in one variable and a slack inequality.
3. The inequality 8 ≥ p + q ≥ 2 is a double linear inequality in two variables.
4. The inequality 2k + 1 ≤ 8 is a numerical inequality.
5. The inequality s > 100 is not a strict inequality.
Answer
1. True.
2. False. The inequality 7p + 3q > 2 is a linear inequality in two variables.
3. True.
4. False. The inequality 2k + 1 ≤ 8 is not a numerical inequality as it involves a variable k.
5. False. The inequality s > 100 is a strict inequality.
Solving Linear Inequalities in One Variable
- Any solution of an inequality in one variable is a value of the variable that makes it a true statement.
- The set of numbers consisting of all the solutions of an inequality is known as the solution set of an inequality.
- The rules that need to be followed to solve an inequality are:
- Equal numbers can be added to (or subtracted from) both sides of an inequality without affecting the sign of the inequality.
- Both sides of an inequality can be multiplied (or divided) with the same positive number. However, when both sides are multiplied or divided by a negative number, then the sign of the inequality is reversed.
- As we saw in the video, the solution set of the inequation −4x − 6 < x + 9 came out to be x ≥ −3. Now, the solution set might be taken from real numbers or whole numbers or integers or any other set of numbers.
- The set from which the values of the variables (involved in the inequation) are chosen is called the replacement set. We may take any set as the replacement set. For example: N, Z,{−4, −3, −2}can be taken as the replacement set.
Depending upon the replacement set, we get the solution set as
|
Replacement |
Solution Set |
|
N |
N |
|
Z |
{-3, -2, -1, 0, 1, 2 ……} |
|
{-4, -3, - 2} |
{-3, -2} |
We can also represent the solution of −4x − 6 < x + 9, x ∈ Z on a number line as follows:
Combining Inequations
Let us consider two inequations 7x + 14 ≥ 21 and −9x > −36; where x ∈ R.
Now 7x + 14 ≥ 21 ⇒ 7x ≥ 21 − 14
⇒ 7x ≥ 7
⇒ x ≥ 1
Also, - 9x > - 36
⇒ - 9x/-9 < -36/-9
⇒ x < 4
Now graph for x ≥ 1:
Also, graph for x < 4 will be :
Thus, the graph of solution set of x ≥ 1 and x < 4 will be :
Let us go through following examples to understand the concept better.
Example 1: Solve: a/3 – 7 ≥ (3a + 1)/2
Answer
a/3 – 7 ≥ (3a + 1)/2
⇒ (a – 21)/3 ≥ (3a + 1)/2
⇒ 2(a – 21) ≥ 3(3a + 1)
⇒ 2a – 42 ≥ 9a + 3
⇒ 2a – 42 – 2a ≥ 9a + 3 – 2a
⇒ -42 ≥ 7a + 3
⇒ -42 – 3 ≥ 7a + 3 – 3
⇒ - 45 ≥ 7a
⇒ a ≤ - 45/7
Thus, all real numbers that are less than or equal to -45/7 are solutions of the given inequality i.e., a ∈ (-∞, -45/7].
Example 2: Show the solution of the inequality 6z/5 – 3 > (3z – 9)/2 > 6 on a number line.
Answer
6z/5 – 3 > (3z – 9)/2 > 6
⇒ (6z – 15)/5 > (3z – 9)/2 > 6
⇒ 2(6z – 15) > 5(3z – 9) > 6 × 5 × 2
⇒ 12z – 30 > 15z – 45 > 60
⇒ 12z – 30 > 15z – 45 and 15z – 45 > 60
⇒ 12z – 30 – 12z > 15z – 45 – 12z and 15z – 45 + 45 > 60 + 45
⇒ - 30 > 3z – 45 and 15z > 105
⇒ - 30 + 45 > 3z – 45 + 45 and 15z/15 > 105/15
⇒ 15 > 3z and z > 7
⇒ 15/3 > 3z/3 and z > 7
⇒ 5 > z and z > 7
Thus, all real numbers which are less than 5 and greater than 7 are the solutions of the given inequality. Thus, the solution of the given inequality can be represented on a number line as
Example 3: Ram, an electrician, cuts a piece of wire in such a manner that the length of the longer piece is three times the length of the shorter piece. What are the possible lengths of the shorter piece if the length of the longer piece is at least 2 cm less than four times the length of the shorter piece?
Answer
Let the length of the shorter piece be x cm.
Also, the length of the longer piece is three times the length of the shorter piece. Hence, the length of the longer piece is 3x cm.
Now, the length of the longer piece is at least 2 cm less than four times the length of the shorter piece, then
3x ≥ 4x − 2
⇒ 3x − 4x ≥ 4x − 2 − 4x
⇒ −x ≥ − 2
⇒ x ≤ 2
Thus, the length of the shorter wire should be less than or equal to 2 cm.