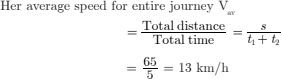NCERT Exemplar Solutions for Class 9 Science Chapter 8 Motion (MCQ, SAQ and LAQ)
Chapter Name | NCERT Exemplar Solutions for Class 9 Science Ch 8 Motion |
Topics Covered |
|
Related Study |
|
Objective Type Questions for Motion
1. A particle is moving in a circular path of radius r. The displacement after half a circle would be :
(a) Zero
(b) 𝛑r
(c) 2r
(d) 2𝛑r
Solution
(c) 2r
2. A body is thrown vertically upward with velocity u, the greatest height h to which it will rise is :
(a) u/g
(b) u2/2g
(c) u2/g
(d) u/2g
Solution
(b) u2/2g
3. The numerical ratio of displacement to distance for a moving object is :
(a) Always less than 1
(b) Always equal to 1
(c) Always more than 1
(d) Equal or less than 1
Solution
(d) Equal or less than 1
4. If the displacement of an object is proportional to square of time, then the object moves with :
(a) Uniform velocity
(b) Uniform acceleration
(c) Increasing acceleration
(d) Decreasing acceleration
Solution
(b) Uniform acceleration
5. From the given v – t graph figure, it can be inferred that the object is :
(a) In uniform motion
(b) At rest
(c) In non-uniform motion
(d) Moving with uniform acceleration
Solution
(a) In uniform motion
6. Suppose a boy is enjoying a ride on a merry-go-round which is moving with a constant speed of 10 m s–1. It implies that the boy is :
(a) At rest
(b) Moving with no acceleration
(c) In accelerated motion
(d) Moving with uniform velocity
Solution
(c) In accelerated motion
7. Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown in figure.
Choose the correct statement :
(a) Car A is faster than car D.
(b) Car B is the slowest.
(c) Car D is faster than car C.
(d) Car C is the slowest.
Solution
(b) Car B is the slowest.
8. Which of the following figure represents uniform motion of a moving object correctly?
9. Area under a v − t graph represents a physical quantity which has the unit:
(a) m2
(b) m
(c) m3
(d) ms–1
Solution
(b) m
10. Slope of a velocity-time graph gives :
(a) The distance
(b) The displacement
(c) The acceleration
(d) The speed
Solution
(c) The acceleration
11. In which of the following cases of motions, the distance moved and the magnitude of displacement are equal?
(a) If the car is moving on straight road.
(b) If the car is moving in circular path.
(c) The pendulum is moving to and fro.
(d) The Earth is revolving around the Sun.
Solution
(a) If the car is moving on straight road.
Short Answer Questions for Motion
12. The displacement of a moving object in a given interval of time is zero. Would the distance travelled by the object also be zero ? Justify your answer.
Solution
No, though the moving object comes back to its initial position the distance travelled is not zero.
13. How will the equations of motion for an object moving with a uniform velocity change?
Solution
In uniform motion, if acceleration (a) = 0 So, 18t equation of motion becomes,
v = u + at
If a = 0 then v = u
If a = 0, 2nd equation of motion becomes,
s = ut + ½at2
⇒ s = ut
If a = 0 , 3rd equation of motion becomes,
v2 – u2 = 2as
⇒ v2 – u2 = 0
14. A girl walks along a straight path to drop a letter in the letterbox and comes back to her initial position. Her displacement-time graph is shown in figure. Plot a velocity-time graph for the same.
Solution
Initial velocity (u) = 0 (As time and displacement are zero.)
Velocity after 50 s, v = Displacement/Time
By substituting the values, we get
v = 100/50 = 2 ms-1
Velocity after 100 s, v = Displacement/Time
Displacement = 0; Time = 100 s
Therefore,
By substituting the values, we get
v = 0/100 = 0
|
V |
0 |
2 |
0 |
|
T |
0 |
50 |
100 |
Velocity – time graph for above data :
15. A car starts from rest and moves along the x-axis with constant acceleration 5 ms–2 for 8 seconds. If it then continues with constant velocity, what distances will the car cover in 12 seconds since it started from the rest?
Solution
As the car moves from rest, therefore, u = 0, a = 5 ms2, t = 8 sec, distance (s) = ?
s’ = ut + ½at2
= 0 + ½ × 5 × (8)2
= 0 + 320/2
= 160 m
To calculate the velocity after 8 sec,
v = u + at
= 0 + 5 × 8 = 40 m/s
So, the distance travelled with this velocity for remaining 4 sec (12 s – 8s = 4s)
s” = 40 × 4 = 160 m
Therefore total distance travelled by the car
= s’ + s”
= 160 +160 = 320 m
16. A motorcyclist drives from A to B with a uniform speed of 30 km h-1 and returns back with a speed of 20 km h–1. Find its average speed.
Solution
Let the distance (AB) = x,
therefore, total distance = x + x = 2x (as it returns back)
Speed = Distance/Time
Therefore, t1 = x/30 ;
t2 (return trip) = x/20
Total time taken = t1 + t2
Total time taken = x /30 + x/20 = 5x/60
Average speed = Total distance/Total time taken = 2x/5x/60
= 2x × 60/5x = 120/5 = 24 km/hr
17. The velocity-time graph figure shows the motion of a cyclist. Find
(i) its acceleration
(ii) its velocity and
(iii) the distance covered by the cyclist in 15 seconds.
Solution
(i) Since velocity is not changing, acceleration is equal to zero.
(ii) Through graph, velocity = 20 m s–1
(iii) Distance covered in 15’ seconds,
s = u × t = 20 x 15 = 300 m
18. Draw a velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height.
Long Answer Questions for Motion
19. An object is dropped from rest at a height of 150 m and simultaneously another object is dropped from rest at a height of 100 m. What is the difference in their heights after 2 s if both the objects drop with same accelerations? How does the difference in heights vary with time?Solution
Initial difference in height
h = (150 – 100) m = 50 m
Both the objects are dropped simultaneously from rest (zero velocity),
Distance travelled by first body in 2 s
d1 = ut + ½at2
Initial speed = 0 (as the object was at rest), t = 2s
Therefore, by substituting the values we get
= 0 + ½ g(2)2 = 2g
= 2 × 9.8 = 19.6 m
Where, g = 9.8
Distance travelled by another body in
2s = d2 = 0 + ½g(2)2
= 2g = 19.6 m
After 2s, height at which the first body will be
h1 = 150 – 19.6
After 2s, height at which the second body will be
h2 = 100 – 19.6
Thus, after 2s, difference in height
= h1 – h2
= 150 – 19.6 – (100 – 19.6)
= 50 m
After 2s, the difference in height will be 50 m = Initial difference in height (h)
Thus, difference in height does not vary with time.
20. An object starting from rest travels 20 m in first 2 s and 160 m in next 4 s. What will be the velocity after 7 s from the start?
Solution
Let’s acceleration of the body be ‘a’.
Therefore, in order to find the acceleration of the body, we use
s = ut + ½at2
Where, u = 0, t = 2s and s = 20m, a = ?
Therefore, by substituting the values we get,
20 = 0 + ½ × a × (2)2
⇒ 20 = ½ × 4a
⇒ a = 20 × 2/4 = 10 m/s
To find final velocity(v), we use
v = u + at
⇒ v = 0 + 10 × 7
⇒ v = 70 m/s
21. Using following data, draw time-displacement graph for a moving object-
|
Time (s) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
Displacement(m) |
0 |
2 |
3 |
4 |
4 |
6 |
4 |
2 |
0 |
Solution
Use this graph to find average velocity for first 4 s, for next 4 s and for last 6 s.
Average velocity = Change in displacement/Total time taken
v = (4-0)/(4-0) = 4/4 = 1 ms-1
For next 4 s, v = (4 – 4)/( 8 – 4)
v = 0/4 = 0 ms-1
As x (metre) remains the same from 4 to 8 seconds, velocity is zero (refer the graph)
For last 6s, V = (0-6)/(16 – 10) = – 1 ms-1
22. An electron moving with a velocity of 5 × 104 m s–1 enters into a uniform electric field and acquires a uniform acceleration of 104 m s–2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover in this time?
Solution
Given,
Initial velocity, u = 5 × 104 ms–1
and acceleration, a = 104 m s–2
(i) Final velocity = v = 2 u
v = 2 × (5 × 104 ms-1)
= 10 × 104 ms-1 ; t = ?
23. Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between 4th and 5th seconds. Using the equation of motion s = ut + ½ at2 .
Solution
24. Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the heights reached by them would be in the ratio of (u1)2 : (u2)2 (Assume upward acceleration is – g and downward acceleration to be + g).
Solution
25. Give one example each of type of motion when :
(a) acceleration is positive.
(b) acceleration is negative.
(c) acceleration is zero.
Solution
(a) When the driver of a car starts motion from rest and increases its velocity, acceleration is positive.
(b) When driver of a running car/train applies brakes so as to stop the car/train, acceleration is negative.
(c) When train is running at constant, velocity along a straight railway track, its acceleration is zero.
26. Draw distance time graph for following situations
(a) When body is stationary.
(b) When body is moving with a uniform speed.
(c) When body is moving with non-uniform speed.
27. State two advantages of plotting velocity – time graph.
Solution
Two advantages of plotting velocity time graph of an object are as follows :
- It tells us variation of velocity of object with time.
- By finding slope of velocity time graph, we can determine the acceleration of object. Similarly, area under velocity time graph gives the value of distance covered by the object during a given time interval.
28. State three equations of motion. Which of them describes :
(a) Velocity – time relation, and
(b) Position – time relation ,
Solution
Three equations of motion are as follows :
- v = u + at
- s = ut + ½ at2
- 2as = v2 – u2
(b) The second equation s = ut + ½ at2 gives the position – time relation .
29. A person travelling in bus noted the timing and the corresponding distances as indicated on the kilometre stones on the road :
|
Time |
8 : 00 am |
8:15 am |
8:30 am |
8: 45 am |
9: 00 am |
|
Distance |
10 km |
20 km |
30 km |
40 km |
50 km |
(a) Name this type of table.
(b) What conclusion do you draw from data ?
Solution
(a) The table is called distance time table.
(b) An analysis of data showed that in every 15 minutes time interval, the bus is covering a distance of 10 km. Thus, the bus is in state of uniform motion having constant speed
v = 10 km/15min = 10/(15/60)h = 40 km/h
30. Examine the data given below formation of two different objects A and B carefully and state whether the motion of the object is uniform or non-uniform. Give reasons.
|
Time |
9:30 am |
9:45 am |
10:00 am |
10:15 am |
10:30 am |
10:45 am |
11:00am |
|
Distance travelled by object A (m) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
Distance travelled by object B (m) |
12 |
19 |
23 |
35 |
37 |
41 |
44 |
Solution
Examination of the given data shows that motion of object A is uniform because it covers equal distances of 10 m each in equal intervals of time of 15 minutes. However, motion of object B is non-uniform because it covers unequal distances in equal intervals of time.
31. Giving one example each, distinguish between uniform acceleration and non-uniform acceleration.
Solution
Acceleration is said to be uniform if velocity of an object changes equally in equal intervals of time. Motion of a freely falling object is uniformly accelerated one at a rate of about 10 m/s.
Acceleration is said to be non-uniform is velocity of an object changes unequally in equal intervals of time. Motion of a vehicle on a crowded street in having non – uniform acceleration.
32. What kind of motion of a body is represented by graphs given along side.
Solution
The graph shown in fig. (a) is a straight line II to time axis and it indicates that the given body is at reset. The graph (b) indicates uniform motion for region CD but thereafter the body comes to rest.
33. What do speed – time graphs shown here indicate ?
Solution
Speed-time graph of fig. (a) represents uniformally accelerated motion having negative acceleration. Speed time graph of fig. (b) represent a non-uniform acceleration.
34. “Displacement of an object is independent of path followed by it.” Justify.
Solution
Displacement of an object depends on its initial position and final position and is independent of the path followed by it because it is the shortest distance from initial position to final position. In adjoining figure we have shown for possible paths for motion from A to B. Although path’s lengths for these paths are different but displacements are exactly same.
35. A particle moves 3 m north, then 4 m east and finally 6 m south. Calculate the magnitude of displacement.
Solution

36. A person moves a distance of 3 km towards east then 2 km towards north and then 3.5 km towards east.
Find :
(a) The distance covered by the person, and
(b) the displacement of his motion.
Solution
As shown AB, BC and CD represent the distance of 3 km east, 2 km north and 3.5 km east respectively.
(a) Net distance covered by a person
= AB + BC + CD
= (3 + 2 + 3.5) km = 8.5 km
(b) Net displacement
37. An athlete completes one round of a circular track of diameter 49 m in 20 s. Calculate the distance covered of displacement at end of 30 s.
Solution
Here, diameter = 49 cmAs an athlete completes one round of a circular track in a period T= 20 s, hence in time t = 30 s, he will complete n = 20/30 = 1.5 rounds. Thus, he will beat point B diagonally opposite to initial position A Displacement = AB = D = 49 m
Distance covered
n(2πr) = n(πD)
= 1.5 × 22/7 × 49
= 231 m
38. An electric train is moving with a velocity of 120 km/h. How much distance will it cover in 30 s?
Solution
Constant velocity of train V = 120 km/h
120 × 5/18 = 100/3 m/s, time t = 30 s
Distance covered
s = vt
= 100/3 × 30 = 1000 = 1.0 km
39. On a 120 km track, a train travels the first 30 km at uniform speed of 30 km/h. Calculate the speed with which the train should move rest of the track so as to get the average speed of 60 km/h for entire trip.
Solution
As the average speed of a train for entire journey
s = 120 km is Vav = 60 km/h
Hence, total time taken by train to cover the journey
40. A girl while riding a bicycle moves with the speed of 10 km/h for 2 hours and with the speed of 15 km/h in next 2 hours. Find the total distance moved by her and her average speed.
Solution Distance moved by girl in time (t1) = 2h with a speed
V1 = 10 km/h is given as
s1 = V1t1 =10 × 2 = 20 km
and distance moved by girl in subsequent time t2 = 3 h
with speed V2 = 15 km/h
is given as :
s2 = V2t2 = 15 x 3 = 45 km
Total distance moved by girl = 20 + 45 = 65
41. A marble rolling on the smooth has a initial velocity of 0.4 m/s. If the floor offers a retardation of 0.02 m/s, calculate the time it will take to come to rest.
Solution
Here initial velocity u = 0.4 m/s, final velocity v = 0, acceleration a = – 0.02 m/s
As per relation v = u + at
42. A cyclist completes 8 revolutions of a circular track of radius 98 m with a uniform speed in 40 minutes. Calculate the speed.
Solution
Here, no. of revolutions completed by the cyclist n = 8, radius of circular track r = 98 and time, t = 40 min = 40 x 60 s = 2400 s Uniform speed of cyclist