NCERT Solution for Class 10 Mathematics Chapter 7 Coordinate Geometry


Chapter Name

NCERT Solution for Class 10 Maths Chapter 7 Coordinate Geometry

Topics Covered

  • Short Revision for the Chapter
  • NCERT Exercise Solution

Related Study

  • NCERT Solution for Class 10 Maths
  • NCERT Revision Notes for Class 10 Maths
  • Important Questions for Class 10 Maths
  • MCQ for Class 10 Maths
  • NCERT Exemplar Questions For Class 10 Maths

Short Revision for Coordinate Geometry

  1. The coordinate axes intersect each other at the origin.
  2. The coordinates of the origin are (0, 0).
  3. The distance of a point from the y – axis is called its x – coordinate (or abscissa).
  4. The distance of a point from the x – axis is called its y – coordinate (or ordinate).
  5. The coordinates of a point on the x – axis are of the form (x, 0).
  6. The coordinates of a point on the y – axis are of the form (0, y).
  7. The graph of ax + by + c = 0 (a, b are not simultaneously zero) is a straight line.
  8. The graph of y = ax2 + bx + c (a≠0) is a parabola.
  9. Distance between the points A(x1 , y1) and B(x2 , y2) is given by 
  10. The distance of a point P(x,y) from the origin O(0,0) is
  11. The coordinates of the point which divides the line segment joining the points A(x1 , y1)and B(x2 , y2) internally, in the ratio m1 : m2 are
  12. The coordinates of the mid – point of the line segment joining the points A(x1 , y1) and B (x2, y2) are
  13. Area of a triangle having the vertices A (x1 , y1)B(x2 , y2) and C (x3 , y3) is given by
  14. If the three points A(x1, y1), B(x2 , y2) and C(x3 , y3) are collinear, then the area of the triangle formed by these points must be zero, i.e. x1(y2 – y3) + x2(y3-y1) + x3(y1-y2) = 0
  15. The coordinates of the centroid of a triangle formed by the points A(x1 , y1), B(x2 , y2) and C(x3 , y3) are

NCERT Exercise Solutions 

Exercise 7.1 

1. Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (- a, – b)


2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.


3. Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.


As we can not get as relation that one distance is equal to sum of other two distance, hence the points are not collinear. 

4. Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.


5. In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.


6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (- 1, – 2), (1, 0), (- 1, 2), (- 3, 0)

(ii) (- 3, 5), (3, 1), (0, 3), (- 1, – 4)


(iii) (4, 5), (7, 6), (4, 3), (1, 2)


7. Find the point on the x-axis which is equidistant from (2, – 5) and (- 2, 9).


8. Find the values of y for which the distance between the points P (2, – 3) and Q (10, y) is 10 units.


9. If Q (0, 1) is equidistant from P (5, – 3) and R (x, 6), find the values of x. Also find the distance QR and PR.

10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (- 3, 4).


Exercise 7.2

1. Find the coordinates of the point which divides the join of (- 1, 7) and (4, – 3) in the ratio 2:3.

2. Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).

Solution

Let P and Q be the points of trisection.
P divides AB in the ratio 1 : 2. 


3. To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the following figure. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?


4. Find the ratio in which the line segment joining the points (-3, 10) and (6, – 8) is divided by (-1, 6).


5. Find the ratio in which the line segment joining A (1, – 5) and B (- 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.


6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.


7. Find the coordinates of a point A, where AB is the diameter of circle whose centre is (2, – 3) and B is (1, 4).


8. If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 3/7 AB and P lies on the line segment AB.


9. Find the coordinates of the points which divide the line segment joining A (- 2, 2) and B (2, 8) into four equal parts.


10. Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2,-1) taken in order.
[Hint: Area of a rhombus = 1/2 (product of its diagonals)


Exercise 7.3 

1. Find the area of the triangle whose vertices are:
(i) (2, 3), (-1, 0), (2, -4)
(ii) (-5, -1), (3, -5), (5, 2)


2. In each of the following find the value of ‘k’, for which the points are collinear.
(i) (7, -2), (5, 1), (3, -k)
(ii) (8, 1), (k, -4), (2, -5)


3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.


4. Find the area of the quadrilateral whose vertices, taken in order, are
(-4, -2), (-3, -5), (3, -2) and (2, 3).


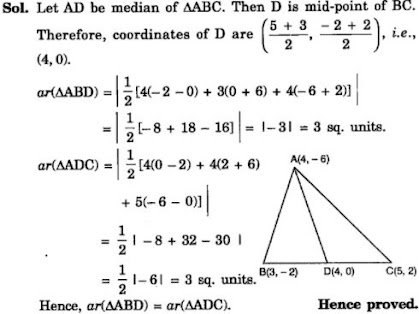
5. You have studied in Class IX that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, – 6), B (3, – 2) and C (5, 2).


Exercise 7.4 

1. Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, –2) and B(3, 7).


2. Find the relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.


3. Find the centre of a circle passing through points (6, -6), (3, -7) and (3, 3).


4. The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.



5. The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular lawn in the plot as shown in the fig. 7.14. The students are to sow the seeds of flowering plants on the remaining area of the plot.
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of triangle PQR if C is the origin?
Also calculate the areas of the triangles in these cases. What do you observe?


6. The vertices of a ∆ ABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that AD/AB = AE/AC = 1/4. Calculate the area of the ∆ ADE and compare it with area of ∆ ABC. (Recall Theorem 6.2 and Theorem 6.6)


⇒ ar(△ADE) : ar(△ABC) = 1:16. 
[Use the result 'if two triangles are similar, then their areas are proportional to the squares of their corresponding sides.']

7. Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ∆ ABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ : QE = 2:1 and CR : RF = 2 : 1.
(iv) What do you observe?
[Note: The point which is common to all the three medians is called the centroid
and this point divides each median in the ratio 2 : 1.]
(v) If A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of triangle ABC, find the coordinates of the centroid of the triangle.


8. ABCD is a rectangle formed by the points A (-1, – 1), B (-1, 4), C (5, 4) and D (5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.

Tags
Previous Post Next Post