Revision Notes for Machines Class 10 Physics ICSE

ICSE Revision Notes for Machines Class 10 Physics

Chapter Name	Machines
Topics Covered	Machines Velocity Ratio Levers Pulley and Combination of Pulley
Related Study	Selina Physics ICSE Solutions for Class 10 Frank ICSE Solutions for Class 10 Physics

Machines 

• Machines help us to perform daily activities in a better efficient way. 
• Functions and uses of simple machines: Machines perform the following functions, and they are useful to us in the following four ways:
  1. In changing the point of application of effort to a convenient point.
  2. In changing the direction of effort to a convenient direction.
  3. For obtaining a gain in speed.
  4. In lifting a heavy load by applying a less effort.
• Machines help us to perform daily activities in a better and efficient way. 
• A machine can be defined as a device by which we can either overcome a large resistive force (or load) at some point by applying a small force (or effort) at a convenient point and in a desired direction or by which we can obtain a gain in speed. 

Terms related to Machines 

• The resistive or opposing force to be overcome by a machine is called load (L). 
• The force applied on the machine to overcome the load is called effort (E). 
• The ratio of the load to the effort is called the mechanical advantage of the machine.
  Mechanical advantage (M.A.) = Load (L)/Effort(E) 
• MA greater than one: In a machine used to overcome a certain load, the effort needed is less than the load. 
• MA less than one: In a machine used to overcome a certain load, the effort needed is greater than the load. 
• MA equal to one: The effort needed is equal to the load.
• A machine with MA greater than one works as a force multiplier, while the machine with MA less than one gives the gain in speed.
• The machine with MA equal to one is generally used to change the direction of effort as there is no gain in force or speed.
• Unit: Because MA is the ratio of two similar quantities, it has no unit.

Velocity Ratio (VR)

• The ratio of the velocity of effort to the velocity of load is called the velocity ratio of a machine.
  Velocity Ratio (V.R.) = Velocity of effort (V_E)/Velocity of load (V_L)
• If d_L and d_E are the distances moved in the same time t by the load and effort, respectively, then
  Velocity of load (V_L) = d_L/t
  Velocity of effort (VE) = d_E/t
  Velocity ratio (V.R.) = d_E/d_L 
• Thus, VR is also defined as the ratio of the displacement of effort to the displacement of load.
• A machine works as a force multiplier if its VR is more than one. 
• Velocity Ratio of a machine is equal to one if the displacement of load is equal to the displacement of effort. Such a machine changes the direction of effort.
• Unit: Because VR is also the ratio of two similar quantities, it has no unit.
• The work done on the machine by the effort is called the work input (W_input).
  Work input = Work done by the effort 
• The work done by the machine on the load is called the work output (W_output).
  Work output = Work done on the load 
• It is the ratio of the useful work done by the machine to the work put into the machine by the effort. In other words, efficiency is the ratio of the work output to the work input. It is denoted by the symbol η (eta).
  Efficiency (η) = Work output (W_output)/(Work input (W_input)
  It is usually expressed in percentage, so we have
  Efficiency (η) = Work output (W_output)/(Work input (W_input) × 100%
• Unit: Because it is a ratio of two similar quantities, it has no unit. 

Principle of a Machine 

• The point at which energy is supplied to a machine by applying effort is called the effort point, and the point where the energy is obtained by overcoming the load is called the load point. 
• The input energy is given as
  Input energy = Work done at the effort point = Effort × displacement of the point of application of effort 
• ∙The output energy is given as 
• Output energy = Work done at the load point = Load × displacement of the point of application of load 
• From the law of conservation of energy, the useful work done by a machine (i.e. output energy) can never be greater than the work done on the machine (i.e. input energy). 
• Thus, no machine can have efficiency greater than 1.
• An ideal machine is one in which there is no loss of energy in any manner. The work output is equal to the work input, i.e. the efficiency of an ideal machine is 100%.
• In an actual machine, the output energy is always less than the input energy as there is some loss of energy during its operation. The loss in energy can be due to the following reasons:
  I. The moving parts in it are neither weightless nor smooth (or frictionless).
  II. The string in it (if any) is not perfectly elastic.
  III. Its different parts are not perfectly rigid. 

Efficiency, MA and VR 

• Thus, MA of a machine is equal to the product of its VR and efficiency. 
• Efficiency = η = Work output/Work input
  η = (L × d_L)/(E × d_E) = L/E × d_L/d_E
  η = M.A/V.R.
  M.A. = V.R × η
• Thus, MA of a machine is equal to the product of its VR and efficiency.

Levers 

• The axis about which the lever turns passes through a point of the lever called the fulcrum. 

Principle of a lever 

• A lever works on the principle of moments.
  Moment of load about the fulcrum = Moment of effort about the fulcrum 
• The two moments are always in opposite direction.
  Load × Load arm = Effort × Effort arm
  L × BF = E × AF
  L/E = AF/BF =  M.A. 
• Thus, we have MA of a lever as the ratio of length of its effort arm to the length of its load arm. This is known as the law of levers. 
• From the above equation,
  I. If effort arm = load arm, then MA = 1.
  II. If effort arm < load arm, then MA < 1.
  III. If effort arm > load arm, then MA > 1.

Kinds of Levers 

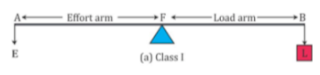
• In case of Class I levers, the fulcrum F is in between the effort E and the load L. 
• For Class I levers, MA and VR can have any value—either greater than 1 or equal to 1 or less than 1.
  
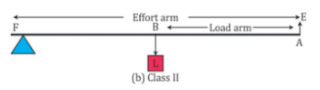
• In case of Class II levers, the load L is somewhere in between the effort and the fulcrum F.
  
• In case of Class II levers, the fulcrum F is in between the effort E and the load L. 
• For Class II levers, the effort arm is always longer than the load arm.
• MA and VR of Class II levers are always more than 1.
• Class II levers always act as a force multiplier.
• In case of Class III levers, the effort E is in between the fulcrum F and the load L, and so the effort arm is always smaller than the load arm.
  
• Therefore, MA < 1, and because MA is equal to VR for an ideal lever, VR < 1 for these levers. 
• MA and VR for Class III levers are always less than 1. 
• With levers of Class III, we do not get gain in force, but we get gain in speed. 

Examples of each Class of Levers as Found in the Human Body 

• Class I lever: Action of nodding of the head. 
• Class II lever: Raising the weight of the body on the toes. 
• Class III lever: Raising a load by the forearm.
  

Pulley 

• A single pulley or a combination of two or more pulleys fixed in a frame is called a block, while a string (rope or chain) which winds around the pulleys in different blocks is known as tackle. 

Single fixed Pulley 

• A pulley which has its axis of rotation fixed in position is called a fixed pulley. It is used for lifting a small load. 
• MA, VR and η of a single fixed pulley
  L = T
  E = T
• M.A. = L/E = 1 
• V. R. = d_L/d_E = 1

Single Movable Pulley 

• A pulley whose axis of rotation is not fixed in position is called a movable pulley. 

MA, VR and η of a single movable pulley

• The load L is balanced by the tension in two segments of the string, and the effort E balances the tension T at the free end. 
• L = T + T = 2T
  E = T 
• M.A. = L/E = 2 
• A single movable pulley acts as a force multiplier.  
• V.R. = d_E/d_L = 2 

Way to change the direction of effort using a movable pulley

• With a single movable pulley, the effort has to be applied in the upward direction. 
• However, it is inconvenient to apply effort in an upward direction; therefore, a movable pulley is used along with a single fixed pulley to change the direction of effort.
  

Combination of Pulleys 

• When a heavy load is to be lifted or shifted from one place to another, we require a pulley system of MA > 2, so a single movable pulley is not enough. A combination of several pulleys is then used. 

1. Using one fixed pulley and other movable pulleys 

• M.A. = L/E = 2³
• In general, if n movable pulleys are connected with one fixed pulley, then
  M.A = 2ⁿ
• If n movable pulleys are connected, then VR is
  V. R = 2ⁿ 

2. Using several fixed pulleys in two blocks (the block and tackle system)

• If the total number of pulleys used in both the blocks is n and the effort is being applied in the downward direction, then the tension in n segments of the string supports the load; therefore, we have M.A. = n
• The effort required to balance the load is
  E = L/n
• V.R. = nd/d = n 
• Thus, VR is always equal to the number of strands of tackle (or sections of the string) supporting the load. 

Effect of weight of pulleys on MA, VR and η 

• Consider a system of n pulleys. Let w be the total weight of the lower block along with the pulleys. 
• In the balanced position,
  M.A. = L/E = (nE - w)/E
  = n - w/E 
• Thus, MA is less than the ideal value n. VR does not change.
• Therefore, efficiency is reduced due to the weight of the lower block of pulleys.