ICSE Revision Notes for Refraction through a Lens Class 10 Physics
Chapter Name | Refraction Through a Lens |
Topics Covered |
|
Related Study |
Refraction through a Lens
Lens
- A lens is a transparent refracting medium bounded by two curved surfaces, of which one or both surfaces are spherical.
Convex or Converging Lens
- A lens with both surfaces bulging outwards is called a double convex lens or simply a convex lens.
- A convex lens converges the light rays incident on it to a point. Hence, a convex lens is also known as a converging lens.
- It may be of three types:
▪ A bi-convex, double-convex or equi-convex lens has both its surfaces convex.
▪ A plano-convex lens has one surface plane and the other surface convex.
▪ A concavo-convex lens has one surface convex and the other surface concave such that it is thicker in the middle than at the periphery.
Concave or Diverging Lens
- A lens with both surfaces curving inwards is called a double concave lens or simply a concave lens.
- A concave lens diverges the light rays incident on it. Hence, a concave lens is also known as a diverging lens.
- It may be of three types:
▪ A bi-concave, double-concave or equi-concave lens has both its surfaces concave.
▪ A plano-convex lens has one surface plane and the other surface concave.
▪ A convexo-concave lens has one surface concave and the other surface convex such that it is thicker at the periphery than at the middle.
Sign convention for measurement of distances
- The origin of the coordinate system for measurement of the distances is the optical centre of the lens.
- In order to make the sign of distances identical to the Cartesian coordinate system, the object is considered to be placed on the left of the lens.
- The axis along which the distances are measured is called as the principal axis. These distances are measured from the optical centre of the lens.
- All the distances which are measured along the direction of the incident ray of the light is taken positive, while the distances opposite to the direction of the incident ray.
- All the lengths that are measured above the principal axis are taken positive, while the length below the principal axis is considered negative.
- The focal length of the convex lens is taken positive and that of concave lens is negative.
Technical Terms Related to Spherical Mirrors
- Centre of curvature: Each surface of a spherical mirror forms a part of a sphere. The centre of this sphere whose part is the lens surface is called the centre of curvature of that surface of the lens. It is represented by C1 and C2.
- Radius of curvature: It is the radius of the sphere of which the part is the lens surface. PC1 and PC2 are the radii of curvature of the convex lens. Similarly, P1C1 and P2C2 are the radii of curvature of the concave lens.
- Principal axis: The horizontal line joining the centre of curvature of the two surfaces of the lens is known as the principal axis.
- Optical centre: It is a point on the principal axis of the lens such that a ray of light passing through this point emerges parallel to its direction of incidence. The optical centre is thus the centre of the lens. A ray of light directed towards the optical centre of a thin lens can be considered as passing undeviated and undisplaced. The optical centre of a thin lens is the point on the principal axis of the lens through which a ray of light passes undeviated.
- Principal foci: A light ray can pass through a lens from either direction. Therefore, a lens has two principal foci which are situated at equal distances from the optical centre, one on either side of the lens. These are known as the first focal point (or first focus) F1 and the second focal point (or second focus) F2.
Principal Rays in Constructing a Ray Diagram
- First rule: A ray of light passing through the optical centre of the lens will emerge without any deviation.
- Second rule: A ray of light incident parallel to the principal axis, after refraction from a convex lens, passes through the second focus F2. In case of a concave lens, the ray appears to diverge from the first focus F1.
- Third rule: A ray of light passing through the first focus, after refraction from a convex lens, will emerge parallel to the principal axis. Whereas a ray of light appearing to meet at the first focus of a concave lens, after refraction, will emerge parallel to the principal axis.
Types of images: The images can be of two types: real and virtual.
- Real image: When the rays from a point of object after refraction through the lens actually meet at a point, the image is real. If a screen is placed at this point, then the image will be formed on it, i.e. a real image can be obtained on a screen.
- Virtual image: When the rays from a point of object after refraction through the lens do not actually meet at a point, but they appear to diverge from a point, the image is virtual. A screen placed at this point will not show any image on it, i.e. a virtual image cannot be obtained on a screen. However, when an eye is kept between the diverging rays, it is able to see the image because the eye lens being convex converges the rays to form the image on its retina.
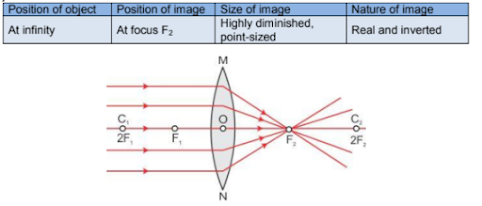
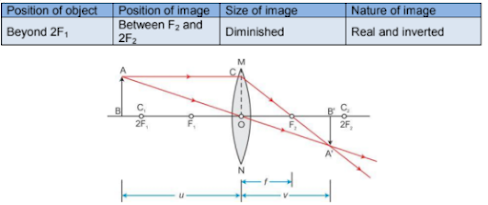
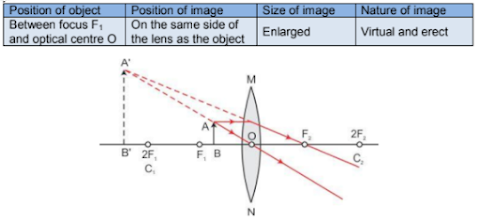
Characteristics and Location of Images for a Convex Lens
Case 1:
Case 2:Case 3:
- The measure of deviation produced by a lens in the path of rays refracted through it is called the power of a lens.
- The power of a lens is defined as the reciprocal of its focal length. It is represented by the letter P. The power P of a lens of focal length f is given as
P = 1/f - The SI unit of power is dioptre (D).
Magnifying Glass or Simple Microscope
Magnifying Power
- The magnifying power of the microscope is defined as the ratio of the ∠B'OA' (= β) subtended by the image A'B' at the eye (or lens) to the ∠DOA' (= α) subtended by A'D at the eye, i.e.
Magnifying power = ∠B'OA'/∠DOA' = 1 + D/f