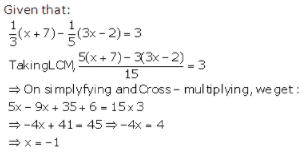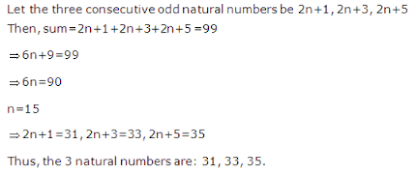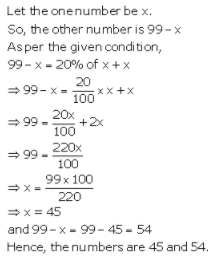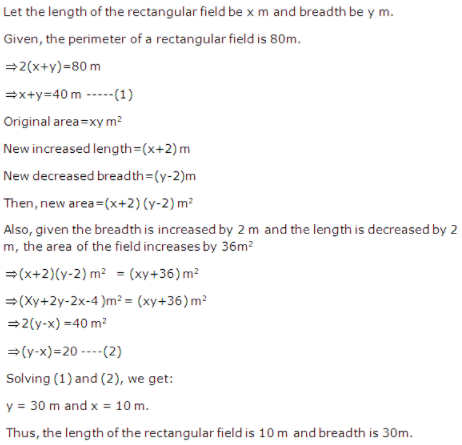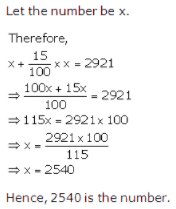Frank Solutions for Chapter 7 Linear Equations Class 9 Mathematics ICSE
Exercise 7.1
1. In the following equations, verify if the given value is a solution of the equation:
(i) 5x – 2 = 18; x = 4
(ii) 2x – 5 = 3x; x = 3
(iii) 3x + 8 = x – 7; x = 3
(iv) (2.1/2) x + (3.1/2) x = 56 – 2x; x = 7
(v) {(3x – 1)/4} + (3/4) = 2; x = 2
Answer
(i) 5x – 2 = 18; x = 4
We know a value is a solution of the equation if it satisfies the equation.
i.e,
x1 is a solution if f (x1) = 0
Here,
x1 = 4
Put in 5x – 2 = 18
We get,
5(4) – 2 = 18
⇒ 20 – 2 =18
⇒ 18 = 18
LHS = RHS
Therefore,
x = 4 is a solution of the equation 5x – 2 = 18
(ii) 2x – 5 = 3x; x = 3
This can be written as:
x = –5
-which is not satisfied by x = 3
Therefore,
x = 3 is not a solution of 2x – 5 = 3x
(iii) 3x + 8 = x – 7; x = 3
This can be written as,
2x + 15 = 0
Now, putting x = 3, we get,
LHS ≠ RHS
Hence,
2(3) + 15 ≠ 0
Therefore, x = 3 is not a solution of the equation 3x + 8 = x – 7
(iv) (2.1/2) x + (3.1/2) x = 56 – 2x; x = 7
On simplifying, we get,
(5/2) x + (7/2)x = 56 – 2x
⇒ (12/2) x + 2x = 56
⇒ 8x = 56
We get,
x = 56/8
⇒ x = 7
By substituting x = 7,
(12/2) 7 + 2(7) = 56
⇒ 42 + 14 = 56
⇒ 56 = 56
We get,
LHS = RHS
Therefore,
x = 7 is a solution of the equation (2.1/2) x + (3.1/2) x = 56 – 2x
(iv) {(3x – 1)/4} + (3/4) = 2; x = 2
On simplifying, we get,
{(3x – 1 + 3)/4} = 2
⇒ (3x + 2) = 8
⇒ 3x = 8 – 2
⇒ 3x = 6
We get,
x = 2
Put x = 2 in above equation,
{(3x – 1)/4} + (3/4) = 2
⇒ {3(2) – 1/4} + (3/4) = 2
⇒ {(6 – 1)/4} + (3/4) = 2
⇒ (5/4) + (3/4) = 2
⇒ (5 + 3)/4 = 2
⇒ 2 = 2
We get,
LHS = RHS
Therefore,
x = 2 is a solution of the equation {(3x – 1)/4} + (3/4) = 2
2. Solve the following equations for the unknown:
(i) 3x + 8 = 35
(ii) 8x – 21 = 3x – 11
(iii) 2x – (3x – 4) = 3x – 4
(iv) 2x + √2 = 3x – 4 – 3√2
(v) 15y – 20 = 2y + 6
(vi) 5x + 10 – 4x + 6 = 12x + 20 – 3x + 12
(vii) (a + 2) (2a + 5) = 2 (a + 1)2 + 13
(viii) (6p + 9)2 + (8p – 7)2 = (10p + 3)2 – 71
(ix) (3x – 1)2 + (4x + 1)2 = (5x + 1)2 + 5
(x) 3 (3x – 4) – 2 (4x – 5) = 6
Answer
(i) 3x + 8 = 35
Collecting like terms,
We get,
3x = 27
⇒ x = 9
(ii) 8x – 21 = 3x – 11
Collecting like terms,
We get,
8x – 3x = 21 – 11
⇒ 5x = 10
⇒ x = 2
(iii) 2x – (3x – 4) = 3x – 4
2x – 3x + 4 = 3x – 4
Collecting like terms,
We get,
2x – 3x – 3x = – 8
⇒ – 4x = – 8
⇒ x = 2
(iv) 2x + √2 = 3x – 4 – 3√2
Collecting like terms,
We get,
x = 4√2 + 4
⇒ x = 4 (√2 + 1)
(v) 15y – 20 = 2y + 6
Collecting like terms,
We get,
13y = 26
⇒ y = 2
(vi) 5x + 10 – 4x + 6 = 12x + 20 – 3x + 12
Collecting like terms,
We get,
x + 16 = 9x + 32
⇒ 8x = – 16
⇒ x = – 2
(vii) (a + 2) (2a + 5) = 2 (a + 1)2 + 13
Collecting like terms,
We get,
a (2a + 5) + 2 (2a + 5) = 2a2 + 4a + 2 + 13
⇒ 2a2 + 5a + 4a + 10 – (2a2 + 4a + 15) = 0
⇒ 5a + 10 – 15 = 0
⇒ 5a = 5
We get,
a = 1
(viii) (6p + 9)2 + (8p – 7)2 = (10p + 3)2 – 71
⇒ {(36p2 + 81 + 2 (6p) (9)} + {(64p2 + 49 – 2 (8p) (7)} = 100p2 + 9 + 2 (10p) (3) – 71
⇒ 100p2 + 130 + 2 × 54p – 2 × 56p = 100p2 + 9 – 71 + 60p
Collecting like terms,
We get,
130 + 71 – 9 = 60p + 4p
⇒ 192 = 64p
We get,
p = 3
(ix) (3x – 1)2 + (4x + 1)2 = (5x + 1)2 + 5
On further calculation, we get,
{(9x2 + 1 + 2 (3x) (1)} + {(16x2 + 1 + 2(4x) (1)} = {(25x2 + 1 + 2 (5x) (1)} + 5
⇒ 25x2 + 2 + 8x + 6x = 25x2 + 6 + 10x
⇒ 14x – 10x = 6 – 2
⇒ 4x = 4
We get,
x = 1
(x) 3 (3x – 4) – 2 (4x – 5) = 6
Simplifying by collecting like terms,
9x – 12 – 8x + 10 = 6
⇒ 9x – 8x = 6 + 12 – 10
We get,
x = 8
3. Solve the following equations for the unknown:
(a) (4x/27) = (8/9)
(b) (1.5y/3) = (7/2)
(c) (-3.4m)/(2.7) = (10.2)/9
(d) (1/2)p + (3/4) p = p – 3
(e) (9y/4) – (5y/3) = (1/5)
(f) (x/2) + (x/4) + (x/8) = 7
(g) (2m/3) – (m/2) = 1
(h) {2 (2x – 1)/9} – {(x – 1)/2} = 0
(i) (4/5) x – 21 = (3/4) x – 20
(j) {(a – 1)/2} – {(a + 1)/3} = 5 – a
Answer
(a) (4x/27) = (8/9)
On cross multiplication, we get,
(4x) (9) = (8) (27)
⇒ x = (8 × 27)/(4 × 9)
⇒ x = (2 × 3)/(1 × 1)
We get,
x = 6
(b) (1.5y/3) = (7/2)
On cross multiplication, we get,
(1.5y) (2) = (7) (3)
⇒ y = (7 × 3)/(1.5 × 2)
⇒ y = (70 × 3)/(15 × 2)
We get,
y = 7
(c) (-3.4m)/(2.7) = (10.2)/9
On cross multiplication, we get,
(-3.4m) (9) = (10.2) (2.7)
⇒ m = –(10.2× 2.7)/(3.4 ×9)
⇒ m = – (102×27)/(34×9×10)
⇒ m = – (3×3)/(1×1×10)
We get,
m = -0.9
(d) (1/2) p + (3/4) p = p – 3
On calculating further, we get,
(1/2) p + (3/4) p – p = – 3
⇒ (p/2) + (3p/4) – p = – 3
On taking L.C.M we get,
{(2p + 3p – 4p)/4} = – 3
⇒ p/4 = – 3
⇒ p = (- 3) (4)
We get,
p = – 12
(e) (9y/4) – (5y/3) = (1/5)
On taking L.C.M. we get,
{(27y – 20y)/12} = (1/5)
⇒ (7y/12) = (1/5)
⇒ (7y) (5) = 12
⇒ y = 12/(7 × 5)
We get,
y = (12/35)
(f) (x/2) + (x/4) + (x/8) = 7
On taking L.C.M. we get,
{(4x + 2x + x)/8} = 7
⇒ (7x/8) = 7
On cross multiplication, we get,
7x = (7) (8)
⇒ x = (7 × 8)/ 7
We get,
x = 8
(g) (2m/3) – (m/2) = 1
On taking L.C.M. we get,
{(4m – 3m)/6} = 1
⇒ 4m – 3m = 6
Hence,
m = 6
(h) {2 (2x – 1)/9} – {(x – 1)/2} = 0
On further calculation, we get,
{(4x – 2)/9} – {(x – 1)/2} = 0
⇒ (4x – 2)/9 = (x – 1)/2
On cross multiplication, we get,
2 (4x – 2) = 9 (x – 1)
⇒ 8x – 4 = 9x – 9
We get,
x = 5
(i) (4/5) x – 21 = (3/4) x – 20
(4/5) x – (3/4) x = – 20 + 21
Taking L.C.M. we get,
(16x/20) – (15x/20) = 1
⇒ {(16x – 15x)/20} = 1
⇒ 16x – 15x = 20
We get,
x = 20
(j) {(a – 1)/2} – {(a + 1)/3} = 5 – a
On further calculation, we get,
{(a – 1)/2} – {(a + 1)/3} + a = 5
On taking the L.C.M. we get,
[{3 (a – 1) – 2 (a + 1) + 6a}/6] = 5
⇒ 3a – 3 – 2a – 2 + 6a = 5 × 6
⇒ 7a – 5 = 30
⇒ 7a = 30 + 5
⇒ 7a = 35
We get,
a = 5
4. Solve the following equations for the unknown:
(a) (5/x) – 11 = (2/x) + 16, x ≠ 0
(b) 11 – (3/x) = (5/x) + 3
(c) {5/(3x – 2)} – (1/8) = 0, x ≠ 0, x ≠ (2/3)
(d) {1/(x – 1)} + (4/5) = (2/3), x ≠ 1
(e) {7/(x – 2)} – (5/3) = 3, x ≠ 2
(f) (2x + 3)/(x + 7) = (5/8), x ≠ – 7
(g) {(3x – 5)/(7x – 5)} = (1/9), x ≠ (5/7)
(h) {3/(x + 1)} – {(x – 6)/(x2 – 1)} = 12/(x – 1)
(i) {(x + 13) / (x2 – 1)} + {5 / (x + 1)} = 7 / (x + 1)
(j) {(6x + 7)/(3x + 2)} = {(4x + 5)/(2x + 3)}
(k) 2.1/5 – {(x – 2)/3} = (x – 1)/3
(l) (1/2) {y – (1/3)} + (1 / 4) {2y + (1/5)} = (3/4) {y – (1/12)}
(m) 2 + {(3x – 2)/(3x + 2)} = (3x + 2)/(x + 1)
(n) {(7x – 1)/4} – (1/3) {2x – (1 – x)/2} = 5.1/3
Answer
(a) (5/x) – 11 = (2/x) + 16, x ≠ 0
(5/x) – (2/x) = 11 + 16
On further calculation, we get,
{(5 – 2)/x} = 27
⇒ (3/x) = 27
⇒ x = (3/27)
We get,
x = (1/9)
(b) 11 – (3/x) = (5/x) + 3
11 – 3 = (5/x) + (3/x)
⇒ (5/x) + (3/x) = 11 – 3
On taking L.C.M. we get,
{(5 + 3)/x} = 11 – 3
⇒ (8/x) = 8
⇒ x = (8/8)
We get,
x = 1
(c) {5/(3x – 2)} – (1/8) = 0, x ≠ 0, x ≠ (2/3)
{5/(3x – 2)} = (1/8)
On cross multiplication, we get,
40 = 3x – 2
⇒ 3x = 40 + 2
⇒ 3x = 42
⇒ x = (42/3)
We get,
x = 14
(d) {1/(x – 1)} + (4/5) = (2/3), x ≠ 1
{1/(x – 1) = (2/3) – (4/5)
On taking L.C.M. we get,
{1/(x – 1)} = (10/15) – (12/15)
⇒ {1/(x – 1)} = (- 2/15)
On cross multiplication, we get,
15 = – 2 (x – 1)
⇒ 15 = – 2x + 2
⇒ 2x = – 13
⇒ x = (- 13/2)
We get,
x = - (6.1/2)
(e) {7/(x – 2)} – (5/3) = 3, x ≠ 2
{7/(x – 2)} = (5/3) + 3
On taking L.C.M. we get,
{7/(x – 2)} = {(5 + 9)/3}
{7/(x – 2)} = (14/3)
On cross multiplication, we get,
21 = 14 (x – 2)
⇒ 21 = 14x – 28
⇒ 14x = 49
⇒ x = (49 / 14)
We get,
x = (7/2)
(f) (2x + 3)/(x + 7) = (5/8), x ≠ – 7
On cross multiplication, we get,
8 (2x + 3) = 5 (x + 7)
⇒ 16x + 24 = 5x + 35
⇒ 16x – 5x = 35 – 24
⇒ 11x = 11
We get,
x = 1
(g) {(3x – 5)/(7x – 5)} = (1/9), x ≠ (5/7)
On cross multiplication, we get,
9 (3x – 5) = 7x – 5
⇒ 27x – 45 = 7x – 5
⇒ 27x – 7x = – 5 + 45
⇒ 20x = 40
We get,
x = 2
(h) {3/(x + 1)} – {(x – 6)/(x2 – 1)} = 12/(x – 1)
{3/(x + 1)} – {(x – 6) (x – 1) (x + 1)} = 12/(x – 1)
Here,
LCM of all the denominators in the equation is (x – 1) (x + 1)
Multiplying throughout by the LCM, we get,
3 (x – 1) – (x – 6) = 12 (x + 1)
⇒ 3x – 3 – x + 6 = 12x + 12
⇒ 3x – 12x – x = 12 – 6 + 3
⇒ –10x = 9
We get,
x = (- 9/10)
(i) {(x + 13)/(x2 – 1)} + {5/(x + 1)} = 7/(x + 1)
{(x + 13)/(x – 1) (x + 1)} + {5/(x + 1)} = 7/(x + 1)
Here,
LCM of all the denominators in the equation is (x – 1) (x + 1)
Multiplying throughout by the LCM, we get,
x + 13 + 5 (x – 1) = 7 (x – 1)
⇒ x + 13 + 5x – 5 = 7x – 7
⇒ 13 – 5 + 7 = 7x – 5x – x
⇒ 20 – 5 = 7x – 6x
We get,
x = 15
(j) {(6x + 7)/(3x + 2)} = {(4x + 5)/(2x + 3)}
On cross multiplication, we get,
(6x + 7) (2x + 3) = (4x + 5) (3x + 2)
⇒ 6x (2x + 3) + 7 (2x + 3) = 4x (3x + 2) + 5 (3x + 2)
On further calculation, we get,
12x2 + 18x + 14x + 21 = 12x2 + 8x + 15x + 10
⇒ 18x + 14x + 21 = 8x + 15x + 10
⇒ 18x – 8x + 14x – 15x = 10 – 21
⇒ 10x – 1x = – 11
⇒ 9x = – 11
We get,
x = (- 11 / 9)
(k) 2.1/5 – {(x – 2)/3} = (x – 1)/3
This can be written as,
(11/5) – {(x – 2)/3} = (x – 1)/3
⇒ (11/5) = {(x – 1)/3} + {(x – 2)/3}
On taking LCM, we get,
(11/5) = {(x – 1 + x – 2)/3}
⇒ (11/5) = (2x – 3)/3
On cross multiplication, we get,
11 (3) = 5 (2x – 3)
⇒ 33 = 10x – 15
⇒ 10x = 33 + 15
⇒ 10x = 48
We get,
x = 4.8
(l) (1/2) {y – (1/3)} + (1/4) {2y + (1/5)} = (3/4) {y – (1/12)}
⇒ (y/2) – (1/6) + (y/2) + (1/20) = (3y/4) – (1/16)
⇒ (y/2) + (y/2) – (3y/4) = – (1/16) + (1/6) – (1/20)
⇒ y – (3y/4) = – (1/16) + (1/6) – (1/20)
On taking LCM, we get,
{(4y – 3y)/4} = {(-15 + 40 – 12)/240}
⇒ (y/4) = (13/240)
⇒ y = (13/240) × 4
We get,
y = (13/60)
(m) 2 + {(3x – 2)/(3x + 2)} = (3x + 2)/(x + 1)
⇒ 2 = {(3x + 2)/(x + 1)} – {(3x – 2)/(3x + 2)}
On taking LCM, we get,
2 = {(3x + 2) (3x + 2) – (3x – 2) (x + 1)}/(x + 1) (3x + 2)
On cross multiplication, we get,
2{(x + 1) (3x + 2)} = (3x + 2) (3x + 2) – (3x – 2) (x + 1)
⇒ 2 {(3x2 + 2x + 3x + 2)} = (9x2 + 6x + 6x + 4) – (3x2 + 3x – 2x – 2)
⇒ 6x2 + 4x + 6x + 4 = 9x2 + 6x + 6x + 4 – 3x2 – 3x + 2x + 2
⇒ 4x = 6x – 3x + 2x + 2
⇒ – x = 2
We get,
x = – 2
(n) {(7x – 1)/4} – (1/3) {2x – (1 – x)/2} = 5.1/3
⇒ {(7x – 1)/4}- {(2x/3) + (1 – x)/6} = (16/3)
Here,
LCM of all the denominators is 12
Multiply the equation throughout by 12, we get,
{3 (7x – 1)/12} – {4 (2x)/12} + {2 (1 – x)/12} = 4 (16)
⇒ {(21x – 3)/12} – {(8x/12)} + {(2 – 2x)/12} = 64
⇒ 21x – 3 – 8x + 2 – 2x = 64
⇒ 11x = 64 + 3 – 2
⇒ 11x = 65
We get,
x = (65/11)
5. Solve the following equations for the unknown:
(a) √x – 5 = 3
(b) 7 – (1/√y) = 0
(c) (1/5) = (3√x /3)
(d) 2 √(x – 3)/(x + 5) = (1/3)
Answer
(a) √x – 5 = 3
Squaring on both sides, we get,
x – 5 = (3)2
⇒ x – 5 = 9
⇒ x = 9 + 5
We get,
x = 14
(b) 7 – (1/√y) = 0
⇒ 7 = (1/√y)
Squaring on both sides, we get,
(7)2 = (1/y)
⇒ 49 = (1/y)
We get,
y = (1/49)
(c) (1/5) = (3√x/3)
⇒ (1/5) = √x
Squaring on both sides, we get,
(1/5)2 = x
We get,
x = (1/25)
(d) 2 √(x – 3)/(x + 5) = (1/3)
On squaring both sides, we get,
{2 √(x – 3)/(x + 5)}2 = (1/3)2
⇒ 4 {(x – 3)/(x + 5)} = (1/9)
⇒ (4x – 12)/(x + 5) = (1/9)
On cross multiplication, we get,
9 (4x – 12) = x + 5
⇒ 36x – 108 = x + 5
⇒ 36x – x = 5 + 108
⇒ 35x = 113
We get,
x = (113/35)
6. Find the value of x for which the expression (x/5) + 2 and (x/3) – 4 are equal.
Answer
Given that the two expressions are equal
i.e,
(x/5) + 2 = (x/3) – 4
On further calculation, we get,
(x/5) – (x/3) = – 4 – 2
On taking LCM, we get,
(3x – 5x)/15 = – 6
⇒ (-2x/15) = – 6
On cross multiplication, we get,
2x = 15 × 6
⇒ 2x = 90
We get,
x = 45
7. Find the value of x if the difference of one-third of (x + 7) and one-fifth of (3x – 2) is 3.
Answer
According to the given statement,
(1/3) (x + 7) – (1/5) (3x – 2) = 3
Taking LCM, we get,
{5 (x + 7) – 3 (3x – 2)}/15 = 3
On cross multiplication, we get,
5x + 35 – 9x + 6 = 3 × 15
⇒ 5x – 9x + 35 + 6 = 45
⇒ – 4x + 41 = 45
⇒ – 4x = 45 – 41
⇒ – 4x = 4
We get,
x = – 1
8. Shweta’s age is six times that of Jayeeta’s age. 15 years hence Shweta will be three times as old as Jayeeta; find their ages.
Answer
Let Jayeeta’s age = x years and
Shweta’s age = 6x years
After 15 years,
As per the given condition,
6x + 15 = 3 (x + 15)
⇒ 6x + 15 = 3x + 45
⇒ 6x – 3x = 45 – 15
⇒ 3x = 30
We get,
x = 10
Jayeeta’s age = x years
= 10 years
Shweta’s age = 6x
= 6 (10)
= 60 years
Therefore, Jayeeta’s age is 10 years and Shweta’s age is 60 years
9. The ages of P and Q are in the ratio 7: 5. Ten years hence, the ratio of their ages will be 9: 7. Find their ages.
Answer
Let the common multiple be x
Hence,
P’s age be 7x years and Q’s age be 5x years
After 10 years,
As per the given condition,
(7x + 10)/(5x + 10) = (9/7)
On cross multiplication, we get,
7 (7x + 10) = 9 (5x + 10)
⇒ 49x + 70 = 45x + 90
⇒ 49x – 45x = 90 – 70
⇒ 4x = 20
We get,
x = 5
P’s age = 7x years
7 (5) = 35 years
Q’s age = 5x
5 (5) = 25 years
Therefore, P’s age is 35 years and Q’s age is 25 years
10. The length of a rectangle is 30 cm more than its breadth. The perimeter of the rectangle is 180 cm. Find the length and the breadth of the rectangle.
Answer
Let the breadth of the rectangle = x cm
So,
The length of the rectangle = (30 + x) cm
According to the given condition,
Perimeter of the rectangle = 180 cm
2 (l + b) = 180
⇒ 2 (30 + x + x) = 180
⇒ 2 (30 + 2x) = 180
⇒ 60 + 4x = 180
⇒ 4x = 180 – 60
⇒ 4x = 120
We get,
x = 30
breadth = x cm
= 30 cm
Length = (30 + x) cm
= (30 + 30) cm
= 60 cm
Therefore, the breadth of the rectangle is 30 cm and the length of the rectangle is 60 cm
11. The perimeter of a rectangle field is 80 m. If the breadth is increased by 2 m and the length is decreased by 2 m, the area of the field increases by 36 m2. Find the length and the breadth of the field.
Answer
Let the breadth of the rectangle = x cm
Perimeter of the rectangle = 80 m
2 (l + x) = 80
⇒ l + x = (80 / 2)
⇒ l + x = 40
We get,
l = 40 – x
So,
The area = lb = x (40 – x)
= 40x – x2
As per the statement,
Breadth = (x + 2) m
Length = (40 – x – 2) m
= (38 – x) m
So,
Area = (38 – x) (x + 2)
= 38x + 76 – x2 – 2x
= – x2 + 36x + 76
Now,
According to the given condition,
– x2 + 36x + 76 – (40x – x2) = 36
⇒ – x2 + 36x + 76 – 40x + x2 = 36
⇒ 36x + 76 – 40x = 36
⇒ 36x – 40x = 36 – 76
⇒ -4x = – 40
We get,
x = 10
So, breadth = x = 10 m and
length = 40 – x = 40 – 10 = 30 m
Therefore, the breadth of the field is 10 m and the length of the field is 30
12. A’s age is six times that of B’s age. 15 years hence A will be three times as old as B;find their ages.
Answer
Let the age of B = x years
Then,
The age of A becomes 6x years
After 15 years,
Age of A = 6x + 15
Age of B = x + 15
Given that, after 15 years, A will be three times as old as B
6x + 15 = 3 (x + 15)
⇒ 6x + 15 = 3x + 45
⇒ 6x – 3x = 45 – 15
⇒ 3x = 30
We get,
x = 10 years
Hence,
Age of B = x = 10 years
Age of A = 6x = 6 (10) = 60 years
13. The present age of a man is double the age of his son. After 8 years, the ratio of their ages will be 7: 4. Find the present ages of the man and his son.
Answer
Let the present age of the son = x years
Then,
The father’s age = 2x years
After 8 years,
Their ages will b (x + 8) years and (2x + 8) years respectively
Given that, after 8 years, the ratio of their ages will be 7: 4
According to the given condition,
(x + 8)/(2x + 8) = (4/7)
On cross multiplication, we get,
7 (x + 8) = 4 (2x + 8)
⇒ 7x + 56 = 8x + 32
⇒ 7x – 8x = 32 – 56
⇒ -x = – 24
We get,
x = 24 years
Therefore, the present age of the son is 24 years and
Age of father = 2x = 2 (24) = 48 years
14. What number increased by 8% of itself gives 1620?
Answer
Let the number be x
Hence,
x + (8/100) × x = 1620
On taking LCM, we get,
(100x + 8x)/100 = 1620
⇒ 108x = 1620 × 100
⇒ x = {(1620 × 100)/108}
We get,
x = 1500
Therefore, the required number is 1500
15. What number increased by 15% of itself gives 2921?
Answer
Let the number be x
Hence,
x + (15/100) × x = 2921
⇒ {100x + 15x)/100} = 2921
On cross multiplication, we get,
115x = 2921 × 100
⇒ x = {(2921 × 100)/115}
We get,
x = 2540
Therefore, the required number is 2540.
16. If m(x – 1) = 40, find the value of m when (x – 1)/2 = 1 + (x + 1)/3
Answer
Exercise 7.2
1. Find the value of x for which the expression x/5 + 2 and x/3 – 4 are equal.
Answer
2. Find the value of x if the difference of one-third of (x + 7) and one-fifth of (3x – 2) is 3.
Answer
3. Find the value of x which makes the expressions 10(3x + 12) and 3(9x + 50) equal to each other.
Answer
4. Find the value of x for which the sum of the expressions 15(x + 1) and 10(x + 2) and 6(x + 3) is 270.
Answer
5. The measures of the angles of a triangle are (3x – 5)°, (3x + 5)° and 6x°. Find x and state that the type of triangle formed.
Answer
6. The measures of the angles of a quadrilateral are: (2x – 4)°, (5x – 10)°, (4x – 8)° and (7x – 14)°. find x.
Answer
7. The angles of a triangle are: 2(x + 6)°, 3(x – 1)° and 6(x + 1)°. find x, and show that the triangle is isosceles.
Answer
8. The side of a square is ½(x + 1) units, and its diagonals is (3 – x)/√2 units. Find the length of a side of the square.
Answer
9. The measures of angles of a triangle are (9x – 5)°, (7x + 5)° and 20x°. Find the value of x. Also show that the triangle is isosceles.
Answer
10. The difference of the squares of two consecutive even natural numbers is 68. Find the two numbers.
Answer
11. For two consecutive odd natural numbers, the square of bigger number exceeds the square of smaller number by 72. Find the two numbers.
Answer
12. The sum of three consecutive natural numbers is 216. Find the numbers.
Answer
13. The sum of three consecutive odd natural numbers is 99. Find the numbers.
Answer
14. Find the number which, when added to its half, gives 60.
Answer
15. Twice a number decreased by 15, equals 25. Find the number.
Answer
16. The sum of two numbers is 50, and their difference is 10. Find the numbers.
Answer
17. A number is as much greater than 21 as it is less than 71. Find the number.
Answer
18. Divide 300 into two parts so that half of the one part is less than the other by 48.
Answer
19. Find two consecutive even numbers, whose sum is 38.
Answer
20. Two complementary angles differ by 14°. Find the angles.
Answer
21. Two angles are supplementary and their measures are (7x + 6)° and (2x – 15)°. Find the measures of the angles.
Answer
22. The measures of angles of a quadrilateral in degrees are x°, (3x – 40)°, 2x° and (4x + 20)°. Find the measure of the angles.
Answer
Answer
24. Two numbers are in the ratio 11: 13. If the smaller number is 286, find the bigger one.
Answer
25. The sum of the squares of two consecutive odd natural numbers is 650. Find the two numbers.
Answer
26. The denominator of a fraction is 18 more than the numerator. If 1 is added to both the numerator and denominator, the value of the fraction equals the value of fraction obtained by adding 8 to the numerator and 15 to the denominator. Find the fraction.
Answer
27. In a two-digit number, the digit at the ten’s place is 4 times the digit at the unit’s place. The sum of the digit and the number is 92. Find the two digit number.
Answer
28. In a two digit number, the ratio of the digits at the unit’s place and the ten’s place is 3:2. If the digits are reversed, the resulting number is 27 more than the original number. Find the two digit number.
Answer
Exercise 7.3
1. Shweta’s age is six times that of Jayeeta’s age. 15 years hence Shweta will be three times as old as Jayeeta; find their ages.
Answer
2. The ages of P and Q are in the ratio 7 : 5. Ten years hence, the ratio of their ages will be 9 : 7. Find their ages.
Answer
3. The present age of a man is double the age of his son. After 8 years, the ratio of their ages will be 7 : 4. Find the present age of the man and his son.
Answer
4. A man covers a distance of 95 km in 5 hours; partly on foot at the rate of 5 km/h and partly on a motorcycle at 40 km/h. Find the distance travelled by him on the motorcycle.
Answer
5. The distance between two places Banglore and Hyderabad is 660 km. Anand starts from Banglore with a certain uniform speed while Sonu starts from Hyderabad at the same time with a uniform speed that is 4 km more than that of Anand. If they meet each other after 5 hours, find the speed of each.
Answer
6. A man went to market at a speed of 4 km/h and returned at a speed of 3 km/h. If he took 30 minutes more in returning. Find the distance of the market from his home.
Answer
7. A takes 4 hours more than B in walking 30 km. If A doubles his speed, he will take 1hr less than B. Find the speed of A and B.
Answer
8. If a motorcyclist drives at the rate of 24 km/h, he reaches his destination 5 minutes too late. If he drives at the rate of 30 km/h, he reaches his destination 4 minutes too soon. How far is his destination?
Answer
9. If a boy walks to his school at a speed of 4 km/h, he reaches the school 10 minutes before time. If he walks at 3 km/h, he reaches the school 10 minutes late. Find the distance between his house and school.
Answer
10. Two planes start from a city and fly in opposite directions, one averaging a speed of 40 km/h more than that of the other. If they are 3400 km apart after 5 hours, find their average speeds.
Answer
11. A streamer goes is downstream from one port to another in 4 hours. It covers the same distance in upstream in 5 hours. If the speed of the stream be 2 km/h, find the distance between the two ports.
Answer
Answer
13. A police car is ordered to chase a speeding car which is 5 km ahead and is travelling at an average speed of 80 km/h. The police car is running at an average speed of 100 km/h. How long it take for the police car to overtake the speeding car?
Answer
Exercise 7.4
1. The length of a rectangle is 30 cm more than its breadth. The perimeter of the rectangle is 180 cm. Find the length and the breadth of the rectangle.
Answer
2. The perimeter of a rectangular field is 80 m. If the breadth is increased by 2 m and the length is decreased by 2 m, the area of the field increases by 36 m2. Find the length and the breadth of the field.
Answer
3. In an isosceles triangle, each of the two equal sides is 4 cm more than the base. If the perimeter of the triangle is 29 cm, find the sides of the triangle.
Answer
4. The perimeter of a rectangular field is 100 m. If its length is decreased by 2 m and breadth increased by 3 m, the area of field is increased by 44 m2. Find the dimensions of the field.
Answer
5. A and B together can complete a piece of work in 6 days. A can do it alone in 10 days. Find the number of days in which B alone can do the work.
Answer
6. A and B together can do a piece of work in 4 days, but A alone can do it in 12 days. How many days would B alone take to do the same piece of work ?
Answer
7. A tap can fill a tank in 12 hours while another tap can fill the same tank in x hours. Both the taps if opened together can fill the tank in 6 hours and 40 minutes. Find the time the second tap will take to fill the tank.
Answer
8: What number increased by 15% of itself gives 2921?
Answer
9. What number decreased by 12% of itself gives 1584?
Answer
10. The sum of two numbers is 99. If one number is 20% more than the others, find the two numbers.
Answer
11. In a factory a worker is paid Rs 20 per hour for normal work and double the rate for overtime work. If he worked for 56 hours in a week, find the number of hours of his normal work if he receives Rs 1440 in all.
Answer
12. A boy played 100 games, gaining Rs 50 on each game that he won, and losing Rs 20 for each game that he lost. If on the whole he gained Rs 800, find the number of games that he won.
Answer
13. In a shooting competition a marksman receives Rs 50 if he hits the mark and pays Rs 20 if he misses it. He tried Rs 100 shots and was paid Rs 100. How many times did he hit the mark?
Answer
14. There are certain benches in a classroom. If 4 students sit on each bench, 3 benches are left vacant; and if 3 students sit on each bench, 3 students are left standing. What is the total number of students in the class ?
Answer
15. A man sells an article and makes a profit of 6%. Had he bought the article at a price 4% less and sold at a price higher by 7.60, he would have made a profit of 12%. Find the cost price.
Answer
16. A man invested Rs 35000, a part of it at 12% and the rest at 14%. If he received a total annual interest of Rs 4460, how much did he invest at each rate?
Answer
17. A 700 g dry fruit pack costs Rs 72. It contains some cashew kernels and the rest as dry grapes. If cashew kernel costs Rs 96 per kg and dry grapes cost Rs 112 per kg, what were the quantities of the two dry fruits separately?
Answer
18. A 12 litre solution is 33.1/% acid. How much water must be added to get the solution having 20% acid?
Answer
19. A man leaves half his property to his wife, one-third to his son, and the remaining to his daughter. If the daughter’s share is Rs 15000, how much money did the man leave? How much money did his wife get?
Answer
Exercise 7.5
1. A’s age is six times that of B’s age. 15 years hence A will be three times as old as B; find their ages.
Answer
2. The ages of A and B are in the ratio 7 : 5. Ten years hence, the ratio of their ages will be 9 : 7. Find their ages.
Answer
3. The present age of a man is double the age of his son. After 8 years, the ratio of their ages will be 7 : 4. Find the present ages of man and his son.
Answer
4. The age of a man is three times the age of his son. After 10 years, the age of the man will be double that of his son. Find their present ages.
Answer
5. The difference between the ages of two brothers is 10 years, and 15 years ago their ages were in the ratio 2 : 1. Find the ratio of their ages 15 years hence.
Answer
6. A boy is now one-third as old as his father. Twelve years hence he will be half as old as his father. Determine the present ages of the boy and that of the father.
Answer
7. 5 years ago, the age of a man was 7 times the age of his son. The age of the man will be 3 times the age of his son. The age of the man will be 3 times the age of his son in 5 years from now. How old are the man and his son now ?
Answer
8. A man is double his son’s age. Twenty years ago, he was six times his son’s age. Find the present age of the father and the son.
Answer
9. The length of a rectangle is 30 more than its breadth. The perimeter of the rectangle is 180 cm. Find the length and breadth of the rectangle.
Answer
10. The perimeter of a rectangular field is 80 m. If the breadth is increased by 2 m and the length is decreased by 2 m, the area of the field increases by 36 m2. Find the length and breadth of the field.
Answer
11. The length of a rectangle is 3 cm more than its breadth. If the perimeter of the rectangle is 18 cm, find the length and breadth of the rectangle.
Answer
12. The perimeter of a rectangular field is 140 m. If the length of the field is increased by 2 m and the breadth decreased by 3 m, the area is decreased by 66 m2. Find the length and breadth of the field.
Answer
13. In an isosceles triangle, each of the two equal sides is 4 cm more than its base. If the perimeter of the triangle is 29 cm, find the sides of the triangle.
Answer
14. The breadth of a rectangular room is 2 m less than its length. If the perimeter of the room is 14 m, find it’s dimensions.
Answer
15. The perimeter of a rectangular field is 100 m. If its length is decreased by 2 m and breadth increased by 3 m, the area of the field is increased by 44 m2. Find the dimensions of the field.
Answer
16. The length of a room exceeds its breadth by 3 m. If both the length and breadth, are increased by 1m, then the area of the room is increased by 18 cm2. Find the length and breadth of the room.
Answer
17. A and B together can complete a piece of work in 6 days. A can do it alone in 10 days. Find the number of days in which B alone can do the work.
Answer
18. A and B together can complete a piece of work in 4 days, but A alone can do it in 12 days. How many days would B alone take to do the same work.
Answer
19. A tap can fill a tank in 12 hrs while another tap can fill the same tank in x hours. Both the taps if opened together fill the tank in 6 hrs and 40 minutes. Find the time the second tap will take to fill the tank.
Answer
20. Tap A can empty a tank in 6 hours. Tap A along with Tap B together can empty the tank in 3.3/7 hours. Find the time Tap B alone will take to empty the tank.
Answer
Exercise 7.6
1. What number increased by 8% of itself gives 1620?
Answer
2. What number increased by 15% of itself gives 2921?
Answer
3. What number decreased by 12% of itself gives 1584?
Answer
4. What number decreased by 18% of itself gives 1599?
Answer
5. In a factory a worker is paid Rs 20 per hour for normal work and double and rate for overtime work. If he worked for 56 hours in a week, find the number of hours of his normal work if he receives Rs 1440 in all.
Answer
6. A worker is employed on the condition that he will be paid Rs 60 for each day that he works and fined Rs 20 for each day that he remains absent. If he is paid Rs 1000 for the month of September, find the number of days that he worked.
Answer
7. A boy played 100 games, gaining Rs 50 on each game that he won, and losing Rs 20 for each game that he lost. If on the whole he gained Rs 800, find the number of games that he won.
Answer
8. In a factory male workers are paid one and a half times more than their female counterparts for each hour of work. In a particular week a husband and wife team worked for a total of 60 hours with the husband working twice as much as his wife. The total amount earned by both is Rs 960. If the husband’s earning is 4 times that of his wife, find the number of hours each worked.
Answer
9. In a shooting competition a marks man receives 50 paise if he hits the mark and pays 20 paise if he misses it. He tried 100 shots and was paid Rs 29. How many times did he hit the mark?
Answer
10. There are certain benches in a classroom. If 4 students on each bench, three benches are left vacant and if 3 students sit on each bench, 3 students are left standing. What is the total number of students in the class?
Answer
11. In a class there are a certain number of seats. If each student occupies one seat, 9 students remain standing and if 2 students occupy one seat, 7 seats are left empty. Find number of seats in the class.
Answer
12. A man sells an article and makes a profit of 6%. Had he bought the article at a price 4% less and sold at a price higher by Rs 7.60, he would have made a profit of 12%. Find his cost price.
Answer
Answer
14. A man invested Rs 35000, a part of it at 12% and the rest at 14%. If he received a total annual interest of Rs 4460, how much did he invest at each rate?
Answer
15. A 700g dry fruit pack costs Rs 72. It contains some cashew kernels and the rest as dry grapes. If cashew kernels cost Rs 96 per kg and dry drapes costs Rs 112 per kg. What were the quantities of the two dry fruits separately.
Answer
16. In an election there were two candidates. A total of 9791 votes were polled. 116 votes were declared invalid. The successful candidate got 5 votes for every 4 votes his opponent had. By what margin did the successful candidate win ?
Answer
17. A 12 litre solution is 33.1/3% acid. How much water must be added to get the solution having 20% acid ?
Answer
18. A 90 kg solution has 10% salt. How much water must be evaporated to have the solution with 20% salt?
Answer
19. How many kilograms of tea at Rs 50 per kg should be mixed with 35 kg of tea costing Rs 60 per kg so as to sell the mixture at Rs 57 per kg without gaining or losing anything in transaction?
Answer
20. A man leaves half his property to his wife, one-third to his son and the remaining to his daughter. If the daughter’s share is Rs 15000, how much money did the man leave? How much money did his wife get?
Answer