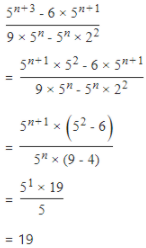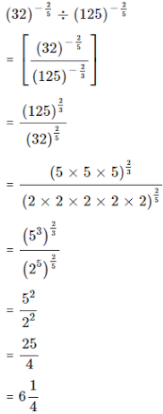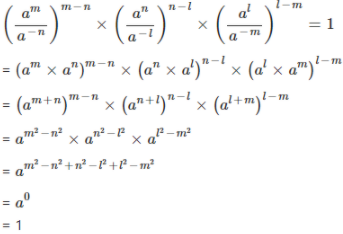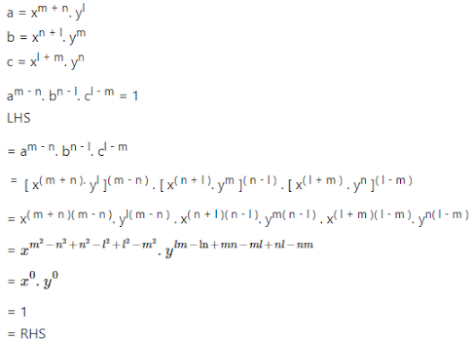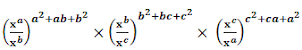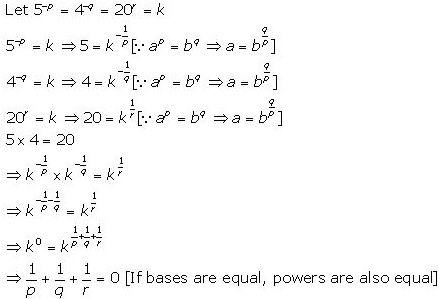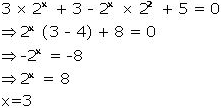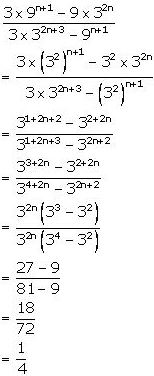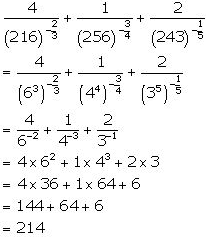ICSE Solutions for Selina Concise Chapter 7 Indices Exponents Class 9 Maths
Exercise 7(A)
1.1 Evaluate : 33 ×(243)2/3 × 91/3
Answer
1.2. Evaluate : 5−4 ×(125)5/3 ÷ (25)1/2
Answer
1.3. Evaluate : (27/125)2/3 × (9/25)−3/2
Answer
1.4. Evaluate : 70 × (25)-3/2 −5−3
Answer
1.5. Evaluate : (16/81)−3/4 × (49/9)3/2 + (343/216)2/3
Answer
2.1. Simplify : (8x3 + 125y3)2/3
Answer
2.2. Simplify : (a+b)−1 . (a−1 + b−1)
Answer
2.3. Simplify : (5n+3 −6×5n+1)/(9×5n × 22)
Answer
2.4. Simplify : (3x2)−3 × (x9)2/3
Answer
3.1. Evaluate : √(1/4) + (0.01)−1/2 – (27)2/3
Answer
3.2. Evaluate : (27/8)2/3 – (1/4)−2 + 5°
Answer
4.1. Simplify the following and express with positive index :
(3−4/2−6)1/4
Answer
4.2. Simplify the following and express with positive index :
(27−3/9−3)1/5
Answer
4.3. Simplify the following and express with positive index :
(32)−2/5 + (125)−2/3
Answer
4.4. Simplify the following and express with positive index :
[1−{1−(1−n)−1}−1]−1
Answer
5. If 2160 = 2a. 3b. 5c, find a, b and c. Hence calculate the value of 3a x 2-b x 5-c.
Answer
6. If 1960 = 2a. 5b. 7c, calculate the value of 2-a. 7b. 5-c.
Answer
1960 = 2a×5b ×7c
⇒ 2×2×2×5×7 ×7 = 2a ×5b×7c
⇒ 23×51 ×72 = 2a ×5b×7c
⇒ 2a×5b×7c = 23 ×51×72
Comparing powers of 2,5 and 7 on the both sides of equation, We have
a = 3; b = 1 and c = 2
Hence,
Value of 2-a×7b× 5-c
= 2-3×71×5-2
7.1. Simplify :
(83a × 25 × 22a)/(4 × 211a ×2−2a)
Answer
7.2. Simplify : (3×27n+1 + 9×33n−1 )/(8×33n – 5×27n)
Answer
8. Show that : (am/a−n)m−n × (an/a−l)n−l × (al/a−m)l−m = 1
Answer
9. If a = xm+n. yl ; b = xn+l. ym and c = xl+m. yn,
Prove that : am–n. bn–l. cl–m = 1
Answer
10.1. Simplify :
Answer
10.2. Simplify :
Answer
Exercise 7(B)
1. Solve for x:
(i) 22x+1 = 8
(ii) 25x-1 = 4 23x+1
(iii) 34x+1 = (27)x+1
(iv) (49)x+4 = 72 (343)x+1
Answer
2. Find x, if:
(i) 42x = 1/32
(ii) √(2x+3) =16
(iii) √(3/5)x+1 = 125/27
(iv) ∛(2/3)x−1 = 27/8
Answer
3. Solve:
(i) 4x–2 – 2x+1 = 0
(ii) 3x2 : 3x = 9:1
Answer
4. Solve :
(i) 8×22x + 4×2x+1 = 1 + 2x
(ii)22x + 2x+2 – 4×23 = 0
(iii) (√3)x-3 = (∜3)x+1
Answer
5. Find the values of m and n if: 42m = (∛16)−6/n = (√8)2
Answer
6. Solve x and y if
(√32)x ÷2y+1 = 1 and 8y – 164−x/2 = 0
Answer
7. Prove that:
(i) (xa/xb)a+b-c × (xb/xc)b+c-a × (xc/xa)c+a-b
(ii) xa(b-c)/xb(a-c) ÷ (xb/xa)c = 1
Answer
8. If ax = b, by = c and cz = a, prove that: xyz = 1.
Answer
9 .If ax = by = cz and b2 = ac, prove that : Y = 2xz/z+x
Answer
10. If 5-P = 4-q = 20r, show that:
Answer
11. If m ≠ n and (m + n)-1 (m-1 + n-1) = mxny, show that:
x + y + 2 = 0
Answer
12. If 5x+1 = 25x–2, find the value of
3x–3 × 23–x
Answer
13. If 4x+3 = 112 + 8×4x, find the value of (18x)3x.
Answer
14. (i) 9x+2 = 720 + 9x
Answer
(ii) Solve for x: (a3x + 5)2. (ax)4 = a8x + 12
Answer
(iii) Solve for x: (81)3/4 –(1/32)−2/5 + x(1/2)−1. 20 = 27
Answer
(iv) Solve for x: 23x + 3 = 23x + 1 + 48
Answer
(v) Solve for x: 3(2x + 1) – 2x + 2 + 5 = 0
Answer
Exercise 7(C)
1. Evaluate
(i) 95/2 – 3×80 –(1/81)−1/2
(ii) (64)2/3 − ∛125 −1/2−5 + (27)−2/3 × (25/9)−1/2
(iii)[(-2/3)-2]3 × (1/3)-4 × 3-1 ×1/6
Answer
2. Simplify: (3×9n+1 −9×32n)/(3×32n+3 −9n+1)
Answer
3. Solve: 3x-1× 52y-3 = 225.
Answer
4. If (a-1b2/a2b-4)7 ÷ (a3b-5/a-2b3)-5 = ax . by find x+y
Answer
5. If 3x+1 = 9x-3, find the value of 21+x.
Answer
6. If 2x = 4y = 8z and 1/2x + 1/4y + 1/8z −4 , find the value of x.
Answer
7. If [9n . 32. 3n –(27)n]/(3m. 2)3 = 3−3 show that m-n =1
Answer
8. Solve for: (13)√x = 44 − 34 −6
Answer
9 . If 34x =(81)-1 and (10)1/y = 0.0001 find the value of : 2-x × 16y .
Answer
10. Solve: 3(2x + 1) – 2x+2 + 5 = 0.
Answer
11. If (am)n = am .an, find the value of: m(n – 1) – (n – 1)
Answer
12. If m = ∛15 and n = ∛14, find the value of m − n− 1/(m2+mn+n2)
Answer
13. Evaluate (2n×6m+1 × 10m-n × 15m+n-2)/(4m ×32m+n × 25m-1)
Answer
14. Evaluate: (xq/x1)1/q1 × (x1/xp)1/1p ×(xp/xq)1/pq
Answer
15 (i). Prove that : a-1/(a-1 + b-1) + a-1/(a-1−b-1) = 2b2/(b2 – a2)
Answer
(ii) Prove that: (a+b+c)/(a-1b-1 + b-1c-1 +c-1a-1) = abc
Answer
16. Evaluate: 4/(216)-2/3 + 1/(256)-3/4 + 2/(243)-1/5