ML Aggarwal Solutions for Chapter 15 Circle Class 9 Maths ICSE
Exercise 15.1
1. Calculate the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13 cm.
Solution
AB is chord of a circle with center O and OA is its radius OM ⊥ AB
Therefore, OA = 13 cm, OM = 12 cm
Now from right angled triangle OAM,
OA2 = OM2 + AM2 by using Pythagoras theorem,
⇒ 132 = 122 + AM2
⇒ AM2 = 132 – 122
⇒ AM2 = 169 – 144
⇒ AM2 = 25
⇒ AM2 = 52
⇒ AM = 5
We know that OM perpendicular to AB
Therefore, M is the midpoint of AB
AB = 2 AM
⇒ AB = 2 (5)
⇒ AB = 10 cm
2. A chord of length 48 cm is drawn in a circle of radius 25 cm. Calculate its distance from the center of the circle.
Solution
AB is the chord of the circle with centre O and radius OA
OM is perpendicular to AB
Therefore, AB = 48 cm
OA = 25 cm
OM ⊥ AB
M is the mid-point of AB
AM = 1/2 AB = ½ × 48 = 24 cm
Now right ∆OAM,
OA2 = OM2 + AM2 (by Pythagoras Axiom)
⇒ (25)2 = OM 2 + (24)2
⇒ OM2 = (25)2 – (24)2 = 625 – 576
⇒ OM2 = 49 = (7)2
⇒ OM = 7 cm
3. A chord of length 8 cm is at a distance of 3 cm from the centre of the circle. Calculate the radius of the circle.
Solution
AB is the chord of a circle with center O
And radius OA and OM ⊥ AB
AB = 8 cm
OM = 3 cm
OM ⊥ AB
M is the mid-point of AB
AM = ½ AB = ½ × 8 = 4 cm.
Now in right ∆OAM
OA2 = OM2 + AM2 (By Pythagoras Axiom)
= (3)2 + (4)2 = 9 + 16 = 25
= (5)2
⇒ OA = 5 cm.
4. Calculate the length of the chord which is at a distance of 6 cm from the centre of a circle of diameter 20 cm.
Solution
AB is the chord of the circle with centre O
And radius OA and OM ⊥ AB
Diameter of the circle = 20 cm
Radius = 20/2 = 10 cm
OA = 10 cm, OM = 6 cm
Now in right ∆OAM,
OA2 = AM2 + OM2 (By Pythagoras Axiom)
⇒ (10)2 = AM2 + (6)2
⇒ AM2 = 102 – 62
⇒ AM2 = 100 – 36 = 64 = (8)2
⇒ AM = 8 cm
OM ⊥ AB
M is the mid-point of AB.
⇒ AB = 2× AM = 2×8 = 16 cm.
5. A chord of length 16 cm is at a distance of 6 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 8 cm from the centre.
Solution
AB is a chord a circle with centre O and
OA is the radius of the circle and OM ⊥ AB
AB = 16 cm, OM = 6 cm
OM ⊥ AB
AM = ½ AB = ½ × 16 = 8 cm
Now in right ∆OAM
OA2 = AM2 + OM2 (By Pythagoras Axiom)
= (8)2 + (6)2
⇒ 64 + 36 = 100 = (10)2
Now CD is another chord of the same circle
ON ⊥ CD and OC is the radius.
In right ∆ONC
OC2 = ON2 + NC2 (By Pythagoras Axioms)
⇒ (10)2 = (8)2 + (NC)2
⇒ 100 = 64 + NC2
⇒ NC 2 = 100 – 64 = 36 = (6)2
⇒ NC = 6
But ON ⊥ AB
N is the mid-point of CD
⇒ CD = 2 NC = 2×6 = 12 cm
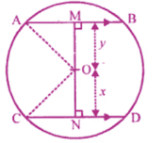
6. In a circle of radius 5 cm, AB and CD are two parallel chords of length 8 cm and 6 cm respectively. Calculate the distance between the chords if they are on :
(i) the same side of the centre.
(ii) the opposite sides of the centre
Solution
Two chords AB and CD of a Circle with centre O and radius OA or OC
OA = OC = 5 cm
AB = 8 cm
CD = 6 cm
OM and ON are perpendiculars from O to AB and CD respectively.
M and N are the Mid-points of AB and
CD respectively
In figure (i) chord are on the same side
And in figure (ii) chord are on the opposite
Sides of the centre
In right ∆OAM
OA2 = AM2 + OM2 (By Pythagoras Axiom)
⇒ (5)2 = (4)2 + OM2
⇒ AM = ½ AB
⇒ 25 = 16 + OM2
⇒ OM2 = 25 – 16 = 9= (3)2
⇒ OM = 3 cm
Again in right ∆OCN,
OC2 = CN2 + ON2
⇒ (5)2 = (3)2 + ON2
⇒ (CN = ½ CD)
⇒ 25 = 9 + ON2
⇒ ON2 = 25 – 9 = 16 = (4)2
⇒ ON = 4
In fig (i), distance MN = ON – OM
= 4 – 3 = 1cm.
In fig (ii)
MN = OM + ON = 3 + 4 = 7 Cm
7. (a) In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle, OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the:
(i) radius of the circle.
(ii) length of chord CD.
(b) In the figure (ii) given below, CD is the diameter which meets the chord AB in E such that AE = BE = 4 cm. If CE = 3 cm, find the radius of the circle.
Solution
(a)Given : AB = 24 cm, OM = 5cm, ON = 12cm
OM ⊥ AB
M is midpoint of AB
AM = 12 cm
(i) Radius of circle OA = √OM2 + AM2
(ii) Again OC2 = ON2 + CN2
⇒ 132 = 122 + CN2
⇒ CN = √(132 – 122) = √(169 – 144) = √25
⇒ CN = 5 cm
As ON ⊥ CD, N is mid-Point of CD
CD = 2CN = 2×5 = 10 cm
(b) AB = 8 cm, EC = 3 cm
Let radius OB = OC = r
OE = (r-3) cm
Now in right ∆OBE
OB2 = BE2 + OE2
⇒ r2 = (4)2 + (r – 3)2
⇒ r2 = 16 + r2 – 6r + 9
⇒ 6r = 25
⇒ r = 25/6 = 4 1/6 cm
8. In the adjoining figure, AB and CD ate two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
Solution
In the figure, chords AB ∥ CD
O is the centre of the circle
Radius of the Circle = 15 cm
Length of AB = 24 cm and CD = 18 cm
Join OA and OC
AB = 24 cm and OM ⊥ AB
AM = MB = 24/2 = 12 cm
Similarly ON ⊥ CD
CN = ND = 18/2 = 9 cm
Similarly In right ∆ CNO
OC2 = CN2 + ON2 (15)2 = (9)2 + ON2
⇒ 225 = 81 + ON2
⇒ ON2 = 225 – 81 = 144 = (12)2
⇒ ON = 12 cm
Now MN = OM + ON = 9 + 12 = 21 cm
9. AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.
Solution
AB and CD are two parallel chords and AB = 10 cm, CD = 4 cm and distance between
AB and CD = 3 cm
Let radius of circle OA = OC = r
OM ⊥ CD which intersects AB in L.
Let OL =x, then OM = x + 3
Now right ∆OLA
OA2 = AL2 + OL2
⇒ r2 = (5)2 + x2 = 25 + x2 (l is mid- point of AB)
Again in right ∆OCM
OC2 = CM2 + OM2
⇒ r2 = (2)2 + (x + 3)2 (M is mid-point of CD)
⇒ r2 = 4 + (x + 3)2 (M is mid-Point of CD)
⇒ r2 = 4 + (x + 3)2
from (i) and (ii)
25 + x2 = 4 + (x + 3)2
⇒ 25 + x2 = 4 + x2 + 9 + 6x
⇒ 6x = 25 – 13 = 12
⇒ x = 12/6 = 2 cm
Substituting the value of x in (i)
r2 = 25 + x2 = 25 + (2)2 = 25 + 4
⇒ r2 = 29
⇒ r = √29cm
Diameter of the circle = 2 r
= 2 ×√29 cm = 2√29 cm
10. ABC is an isosceles triangle inscribed in a circle. If AB = AC = 12√5 cm and BC = 24 cm, find the radius of the circle.
Solution
AB = AC 12√5 and BC = 24 cm.
Join OB and OC and OA
Draw AD ⊥ BC which will pass through
Centre O
OD bisect BC in D
BD = DC = 12 cm
In right ∆ABD
AB2 = AD2 + BD2
⇒ (12√5)2 = AD2 + BD2
⇒ (12√5)2 = AD2 + (12)2
⇒ 144×5 =AD2 + 144
⇒ 720 – 144 = AD2
⇒ AD2 = 576
⇒ AD = √576 = 24
Let radius of the circle = OA = OB = OC = r
OD = AD – AO = 24 – r
Now in right ∆OBD,
OB2 = BD2 + OD2
⇒ r2 = (12)2 + (24 – r)2
⇒ r2 =144 + 576 + r2 – 48r
⇒ 48r = 720
⇒ 48r = 720
⇒ r = 720/48 = 48r
⇒ 48r = 720
⇒ r = 720/48 = 15cm.
Radius = 15 cm.
11. An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.
Solution
ABC is an equilateral triangle inscribed in a
Circle with centre O. Join OB and OC,
From A, Draw AD ⊥ BC which will pass
Through the centre O of the circle.
Each side of ∆ABC = 6 cm.
AD = √3/2 a= √3/2 × 6 = 3 √3 cm.
OD = AD – AO = 3√3 – r
Now in right ∆OBD
OB2 = BD2 + OD2
⇒ r2 = (3)2 + (3√3-r)2
⇒ r2 = 9 + 27 + r2 -6√3r (D is mid-point of BC)
⇒ 6√3r = 36
⇒ R = 36/6√3 = 6/√3 × √3/√3 = 6√3/3 = 2√3 cm
Radius = 2√3 cm
12. AB is a diameter of a circle. M is a point in AB such that AM = 18 cm and MB = 8 cm. Find the length of the shortest chord through M.
Solution
AM = 18 cm and MB = 8 cm
AB = AM + MB = 18 + 8 = 26 cm
Radius of the circle = 26/2 = 13 cm
Let CD is the shortest chord drawn through M.
CD ⊥ AB
Join OC
OM = AM – AO = 18 – 13 = 5 cm
OC = OA = 13 cm
Now in right ∆OMC
OC2 = OM2 + MC2
⇒ (13)2 = (5)2 + MC2 (MC2 = 132 – 52
⇒ MC2 = 169 – 25 = 144 = (12)2
⇒ MC = 12
M is Mid-Point of CD
CD = 2 ×MC = 2×12 = 24 cm
Exercise 15.2
1. If arcs APB and CQD of a circle are congruent, then find the ratio of AB: CD.
Solution
arc APB = arc CQD (given)
AB = CD (If two arcs are congruent, then their corresponding chords are equal)
Ratio of AB and CD = AB / CD = AB /AB = 1/1
AB : CD = 1 : 1
2. A and B are points on a circle with centre O. C is a point on the circle such that OC bisects ∠AOB, prove that OC bisects the arc AB.
Solution
Given : in a given circle with centre O,A
And B are Two points on the circle. C i
another point on the circle such that
∠AOC = ∠BOC
To prove : arc AC = arc BC
Proof: OC is the bisector of ∠AOB
⇒ ∠AOC = ∠BOC
But these are the angle subtended by the arc AC and BC
arc AC = arc BC.
3. Prove that the angle subtended at the centre of a circle is bisected by the radius passing through the mid-point of the arc.
Solution
Given: AB is the arc of the circle with
Centre O and C is the mid-Point od arc AB.
To prove: OC bisects the ∠AOB
I,e ∠AOC = ∠BOC
Proof:
C is the mid-point of arc AB.
arc AC = arc BC
But arc AC and arc BC subtend ∠AOC and
∠BOC at the centre
∠AOC = ∠BOC
Hence, OC Bisects the ∠AOB.
4. In the given figure, two chords AB and CD of a circle intersect at P. If AB = CD, prove that arc AD = arc CB.
Solution
Given: two chord AB and CD of a Circle
Intersect at P and AB = CD
To prove : arc AD = arc CB
Proof:
AB = CD (given)
minor arc AB = minor arc CD
Subtracting arc BD from both sides
arc AB = arc BD = arc CD – arc BD
⇒ arc AD = arc CD
Chapter test
1. In the given figure, a chord PQ of a circle with centre O and radius 15 cm is bisected at M by a diameter AB. If OM = 9 cm, find the lengths of : (i) PQ (ii) AP (iii) BP
Solution
Given, radius = 15 cm
OA = OB = OP = OQ = 15 cm
Also, OM = 9 cm
MB = OB – OM = 15 – 9 = 6 cm
AM = OA + OM =15 + 9 cm = 24 cm
In ∆OMP,
By using Pythagoras Theorem,
OP2 = OM 2 + PM2
⇒ 152 = 92 + PM2
⇒ PM2 = 255 – 81
⇒ PM = √144 = 12 cm
Also, In ∆OMQ
By using Pythagoras Theorem
OQ2 = OM2 + QM2
⇒ 152 = OM2 + QM2
⇒ 152 = 92 + QM2 (QM2 = 225 – 81)
⇒ QM = √144 = 12 cm
⇒ PQ = PM + QM (As radius is bisected at M)
⇒ PQ = 12 + 12 cm = 24 cm
(ii) Now in ∆APM
AP2 = AM2 + OM2
⇒ AP2 =242 + 122
⇒ AP2 = 576 + 144
⇒ AP = √720 = 12 √5 cm
(iii) Now in ∆BMP
BP2 = BM2 + PM2
BP2 = 62 + 122
⇒ BP2 = 36 + 144
⇒ BP = √180 = 6√5 cm
2. The radii of two concentric circles are 17 cm and 10 cm ; a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.
Solution
A line PQRS intersects the outer circle at P
And S and inner circle at Q and R radius of
Outer circle OP = 17 cm and radius of inner
Circle OQ = 10 cm
QR = 12 cm
From O, draw OM ⊥ PS
QM = ½ QR = ½ × 12 = 6 cm
In right ∆OQM
OQ2 = OM2 + QM2
⇒ (10)2 = OM2 + (6)2
⇒ OM2 = 102 – 62
⇒ OM2 = 100 – 36 = 64 = (8)2
⇒ OM = 8 cm
Now in right ∆OPM
OP2 OM2 + PM2
⇒ (17)2 = OM2 + PM2
⇒ PM2 = (17)2 – (8)2
⇒ PM2 = 289 – 64 = 225 = (15)2
⇒ PM = 15 cm
⇒ PQ = PM – QM = 15 – 6 = 9 cm