ICSE Solutions for Chapter 13 Section and Midpoint Formula Class 10 Mathematics
Solution 1: Given, BP:PC = 3:2
Using section formula, the co-ordinates of point P are
[(3×5 + 2×0)/(3 + 2), (3×10 + 2×5)/(3 + 2)]
= (15/5, 40/5)
= (3, 8)
Using distance formula, we have:

Question 2: Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
Solution 2: Mid-point of AB = (2, 3)
∴ {(3 + x)/2, (5 + y)/2} = (2, 3)
⇒ (3 + x)/2 and (5 + y)/2 = 3
⇒ 3 + x = 4 and 5 + y = 6
⇒ x = 1 and y = 1
Question 3: In what ratio is the line joining (2, -4) and (-3, 6) divided by the y-axis.
Solution 3: Let the line joining points A (2, -4) and B(-3, 6) be divided by point P (0, y) in the ratio k:1.
x = (kx2 + x1)/(k + 1)
0 = {(k×(-3) + 1×2)/(k + 1)}
0 = - 3k + 2
k = 2/3
Thus, the required ratio is 2 : 3.
Question 4: In what ratio does the point (1, a) divided the join of (-1, 4) and (4, -1)? Also find the value of a.
Solution 4:

Using section formula, we have:
1 = (4k – 1)/(k + 1),
⇒ k + 1 = 4k – 1
⇒ 2 = 3k
⇒ k = 2/3 …(1)
⇒ a = (-k + 4)/(k + 1)
⇒ a = (-2/3 + 4)/(2/3 + 4) (from 1)
⇒ a = 10/5 = 2
Hence, the required ratio is 2:3 and the value of a is 2.
Question 5: P(-3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.

Solution 5: Point A lies on y-axis, so let its co-ordinates be (0, y).
Point B lies on x-axis, so let its co-ordinates be (x, 0).
P (-3, 2) is the mid-point of line segment AB.
∴ (-3, 2) = {(0 + x)/2, (y + 0)/2}
⇒ (-3, 2) = (x/2, y/2)
⇒ -3 = x/2 and 2 = y/2
⇒ -6 = x and 4 = y
Thus, the co-ordinates of points A and B are (0,4) and (-6, 0) respectively.
Question 6: In what ratio is the line joining A (0, 3) and B (4, -1) divided by the x-axis? Write the co-ordinates of the point where AB intersects the x-axis.
Solution 6: Let the line segment AB intersects the x-axis by point P(x, 0) in the ratio k : 1.
∴ (x, 0) = {(k×4 + 1×0)/(k + 1) , (k×-1 + 1×3)/(k +1)}
(x, 0) = {4k/(k + 1), (-k + 3)/(k + 1)}
⇒ 0 = (-k + 3)/(k + 1)
⇒ k = 3
Thus, the required ratio in which P divides AB is 3 : 1.
Also, we have:
x = 4k/(k + 1)
x = (4 × 3)/(3 + 1) = 12/4 = 3
Thus, the co-ordinates of point P are (3, 0).
Question 7: The mid-point of the segment AB, as shown in diagram, is C (4,-3). Write down the co-ordinates of A and B.
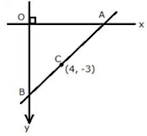
Solution 7: Since, point A lies on x-axis, let the co-ordinates of point A be (x, 0).
Since, point B lies on y-axis, let the co-ordinates of point B be (0, y).
Given, mid-point of AB is C (4, -3).
∴ (4, -3) = {(x + 0)/2, (0 + y)/2}
⇒ (4, -3) = (x/2, y/2)
⇒ 4 = x/2 and -3 = y/2
⇒ x = 8 and y = -6
Thus, the co-ordinates of point A are (8, 0) and the co-ordinates of point Bare (0, -6).
Question 8: Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
Solution 8:
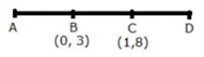
So, B is the mid-point of AC. Let the co-ordinates of point A be (x, y).
∴ (0, 3) = {(x + 1)/2, (y + 8)/2}
⇒ 0 = (x + 1)/2 and 3 = (y + 8)/2
⇒ 0 = x + 1 and 6 = y + 8
⇒ -1 = x and –2 = y
Thus, the co-ordinates of point A are (-1,-2).
Also, C is the mid-point of BD. Let the co-ordinates of point D be (p, q).
∴ (1, 8) = {(0 + p)/2 , (3 + q)/2}
⇒ 1 = (0 + p)2 and 8 = (3 + q)/2
⇒ 2 = 0 + p and 16 = 3 + q
⇒ 2 = p and 13 = q
Thus, the co-ordinates of point D are (2, 13).
Question 9: The line joining the points A (-3,-10) and B (-2, 6) is divided by the point P such that PB/AB = 1/3. Find co-ordinates of P.
Solution 9: Let the co-ordinates of point P are (x, y).

∴ PB:PA = 1:4
Coordinates of P are
(x, y) = {(4×(-2) + 1×(-3))/5, (4×6 + 1×(-10))/5}
= (-11/5, 14/5)
Question 10: The mid-point of the line-segment joining (4a, 2b - 3) and (-4, 3b) is (2, -2a). Find the values of a and b.
Solution 10: It is given that the mid-point of the line-segment joining (4a, 2b - 3) and
(-4, 3b) is (2, -2a)
∴ (2, -2a) ={(4a – 4)/2, (2b – 3 + 3b)/2}
⇒ 2 = (4a – 4)/2
⇒ 4a = 4 - 4
⇒ 4a = 8
⇒ a = 2
Also,
-2a = (2b – 3 + 3b)/2
⇒ -2×2 = (5b – 3)/2
⇒ 5b – 3 = -8
⇒ 5b = -5
⇒ b = -1
⇒ 2 = (4a – 4)/2
⇒ 4a = 4 - 4
⇒ 4a = 8
⇒ a = 2
Also,
-2a = (2b – 3 + 3b)/2
⇒ -2×2 = (5b – 3)/2
⇒ 5b – 3 = -8
⇒ 5b = -5
⇒ b = -1

