ICSE Solutions for Chapter 18 Tangents and Intersecting Chords Class 10 Mathematics
Solution 1:

To prove: OM < ON
Proof: Join OA and OC.
In Rt. ΔAOM,
AO2 = AM2 + OM2
⇒ r2 = (1/2AB)2 + OM2
⇒ r2 = 1/4AB2 + OM2 ...(i)
Again in Rt. ΔONC,
OC2 = NC2 + ON2
⇒ r2 = (1/2 OD)2 + ON2
⇒ r2 = (1/4OD)2 + ON2 ...(ii)
From (i) and (ii)
1/4AB2 + OM2 = 1/4CD2 + ON2
But, AB > CD (given)
∴ ON > OM
⇒ OM < ON
Hence, AB is nearer to the centre than CD.
Question 2: In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm.
Find
(i) AB.
(ii) the length of tangent PT.

Solution 2:
(i) PA = AB + BP = (AB + 4) cm
PC = PD + CD = 5 + 7.8 = 12.8 cm
Since PA × PB = PC x PD
⇒ (AB + 4) × 4 = 12.8 ×5
⇒ (AB + 4) = (12.8 × 5)/4
⇒ AB + 4 = 16
⇒ AB = 12 cm
(ii) Since PT2 = PC × PD
⇒ PT2 = 12.8× 5
⇒ PT2 = 64
⇒ PT = 8 cm
Question 3: In the following figure, PQ is the tangent to the circle at A. DB is a diameter and O is the centre of the circle. If
∠ADB = 30° and ∠CBD = 60°: calculate:
(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB

Solution 3: (i) PAQ Is a tangent and AB is the chord.
∠QAB = ∠ADB = 30° (angles in the alternate segment)
⇒ PT2 = 12.8× 5
⇒ PT2 = 64
⇒ PT = 8 cm
Question 3: In the following figure, PQ is the tangent to the circle at A. DB is a diameter and O is the centre of the circle. If
∠ADB = 30° and ∠CBD = 60°: calculate:
(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB

Solution 3: (i) PAQ Is a tangent and AB is the chord.
∠QAB = ∠ADB = 30° (angles in the alternate segment)
(ii) OA - OD (radli of the same circle)
∴ ∠OAD = ∠ODA = 30°
But, OA ⊥ PQ
∴ ∠PAD - ∠OAP - ∠OAD = 90° - 30° = 60°
∴ ∠OAD = ∠ODA = 30°
But, OA ⊥ PQ
∴ ∠PAD - ∠OAP - ∠OAD = 90° - 30° = 60°
(iii) BD is the diameter.
∴ ∠BCD = 90° (angle in a semi-circle)
Now in ΔBCD,
∠CDB + ∠CBD + ∠BCD = 180°
⇒ ∠CDB + 60° + 90° = 180°
⇒ CDB = 180° - 150° = 30°
Question 4: Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Solution 4:

From Q, QA and QP are two tangents to the circle with centre O
Therefore, QA – QP ...(i)
Similarly, from Q, QB and QP are two tangents to the circle with centre O’.
Therefore, QB = QP ...(ii)
From (i) and (ii)
QA = QB
Therefore, tangents QA and QB are equal.
Question 5: Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
Solution 5:
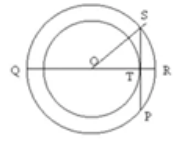 OS = 5 cm
OS = 5 cm
OT = 3 cm
In Rt. Triangle OST
By Pythagoras Theorem,
ST2 = OS2 – OT2
ST2 = 25 - 9
ST2 = 16
ST = 4 cm
Since OT is perpendicular to SP and OT bisects chord SP
So, SP = 8 cm
Question 6: Three circles touch each other externally. A triangle is formed when the centers of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.
Solution 6:
 AB = 6 cm, AC = 8 cm and BC = 9 cm
AB = 6 cm, AC = 8 cm and BC = 9 cm
Let radii of the circles having centers A, B and C be r1, r2 and r3 respectively.
r1 + r3 = 8
r3 + r2 = 9
r2 + r1 = 6
Adding
r1 + r3 + r3 + r2 + r2 + r1 = 8 + 9 + 6
2(r1 + r2 + r3) = 23
r1 + r2 + r3 = 11.5 cm
r1 + 9 = 11.5 (Since r2 + r3 = 9)
r1 = 2.5 cm
r2 + 6 = 11.5 (Since r1 + r3 = 6)
r2 = 5.5 cm
r3 + 8 = 11.5 (Since r2 + r1 = 8)
r3 = 3.5 cm
Hence, r1 = 2.5 cm, r2 = 5.5 cm and r3 = 3.5 cm
Question 7: If the sides of a quadrilateral ABCD touch a circle, prove that AB + CD = BC + AD.
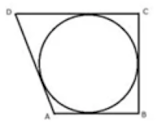
Solution 7:

Let the circle touch the sides AB, BC, CD and DA of quadrilateral ABCD at P, Q, R and S respectively.
Since AP and AS are tangents to the circle from external point A
AP = AS ....(i)
Similarly, we can prove that:
BP = BQ ...(ii)
CR = CQ ...(iii)
DR = DS ...(iv)
Adding,
AP + BP + CR + DR = AS + DS + BQ + CQ
AB + CD = AD + BC
Hence, AB + CD = AD + BC
Question 8: Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that: ∠CPA = ∠DPB
 Solution 8:
Solution 8:

Draw a tangent TS at P to the circles given.
Since TPS is the tangent, PD is the chord.
∴ ∠PAB = ∠BPS ...(i) (angles in alternate segment)
Similarly,
∠PCD = ∠DPS ...(ii)
Subtracting (i) from (ii)
∠PCD - ∠PAB = ∠DPS - ∠BPS
But in ΔPAC,
Ext. ∠PCD = ∠PAB + ∠CPA
∴ ∠PAB + ∠CPA - ∠PAB = ∠DPS - ∠BPS
⇒ ∠CPA = ∠DPB
Question 9: In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Solution 9:

∠ADB = ∠ACB ...(i) (angles in same segment)
Similarly,
∠ABD = ∠ACD ...(ii)
But, ∠AOB = ∠ACD (AC is bisector of ∠BCD)
∴ ∠ADB = ∠ABD (from i and ii)
TAS is a tangent and AB is a chord
∴ ∠BAS = ∠ADB (angles in alternate segment)
But, ∠ADB = ∠ABD
∴ ∠BAS = ∠ABD
But these are alternate angles
Therefore, TS∥BD.
Question 10: In the figure, if AB = AC then prove that BQ = CQ.

Solution 10:
Since, from A, AP and AR are the tangents to the circle
Therefore, AP = AR
Similarly, we can prove that
BP = BQ and CR = CQ
Adding,
AP + BP + CQ = AR + BQ + CR
(AP + BP) + CQ = (AR + CR) + BQ
AB + CQ = AC + BQ
But AB = AC
Therefore, CQ = BQ or BQ = CQ
∴ ∠BCD = 90° (angle in a semi-circle)
Now in ΔBCD,
∠CDB + ∠CBD + ∠BCD = 180°
⇒ ∠CDB + 60° + 90° = 180°
⇒ CDB = 180° - 150° = 30°
Question 4: Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Solution 4:

From Q, QA and QP are two tangents to the circle with centre O
Therefore, QA – QP ...(i)
Similarly, from Q, QB and QP are two tangents to the circle with centre O’.
Therefore, QB = QP ...(ii)
From (i) and (ii)
QA = QB
Therefore, tangents QA and QB are equal.
Question 5: Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
Solution 5:

OT = 3 cm
In Rt. Triangle OST
By Pythagoras Theorem,
ST2 = OS2 – OT2
ST2 = 25 - 9
ST2 = 16
ST = 4 cm
Since OT is perpendicular to SP and OT bisects chord SP
So, SP = 8 cm
Question 6: Three circles touch each other externally. A triangle is formed when the centers of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.
Solution 6:

Let radii of the circles having centers A, B and C be r1, r2 and r3 respectively.
r1 + r3 = 8
r3 + r2 = 9
r2 + r1 = 6
Adding
r1 + r3 + r3 + r2 + r2 + r1 = 8 + 9 + 6
2(r1 + r2 + r3) = 23
r1 + r2 + r3 = 11.5 cm
r1 + 9 = 11.5 (Since r2 + r3 = 9)
r1 = 2.5 cm
r2 + 6 = 11.5 (Since r1 + r3 = 6)
r2 = 5.5 cm
r3 + 8 = 11.5 (Since r2 + r1 = 8)
r3 = 3.5 cm
Hence, r1 = 2.5 cm, r2 = 5.5 cm and r3 = 3.5 cm
Question 7: If the sides of a quadrilateral ABCD touch a circle, prove that AB + CD = BC + AD.

Solution 7:

Let the circle touch the sides AB, BC, CD and DA of quadrilateral ABCD at P, Q, R and S respectively.
Since AP and AS are tangents to the circle from external point A
AP = AS ....(i)
Similarly, we can prove that:
BP = BQ ...(ii)
CR = CQ ...(iii)
DR = DS ...(iv)
Adding,
AP + BP + CR + DR = AS + DS + BQ + CQ
AB + CD = AD + BC
Hence, AB + CD = AD + BC
Question 8: Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that: ∠CPA = ∠DPB


Draw a tangent TS at P to the circles given.
Since TPS is the tangent, PD is the chord.
∴ ∠PAB = ∠BPS ...(i) (angles in alternate segment)
Similarly,
∠PCD = ∠DPS ...(ii)
Subtracting (i) from (ii)
∠PCD - ∠PAB = ∠DPS - ∠BPS
But in ΔPAC,
Ext. ∠PCD = ∠PAB + ∠CPA
∴ ∠PAB + ∠CPA - ∠PAB = ∠DPS - ∠BPS
⇒ ∠CPA = ∠DPB
Question 9: In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Solution 9:

∠ADB = ∠ACB ...(i) (angles in same segment)
Similarly,
∠ABD = ∠ACD ...(ii)
But, ∠AOB = ∠ACD (AC is bisector of ∠BCD)
∴ ∠ADB = ∠ABD (from i and ii)
TAS is a tangent and AB is a chord
∴ ∠BAS = ∠ADB (angles in alternate segment)
But, ∠ADB = ∠ABD
∴ ∠BAS = ∠ABD
But these are alternate angles
Therefore, TS∥BD.
Question 10: In the figure, if AB = AC then prove that BQ = CQ.

Solution 10:
Since, from A, AP and AR are the tangents to the circle
Therefore, AP = AR
Similarly, we can prove that
BP = BQ and CR = CQ
Adding,
AP + BP + CQ = AR + BQ + CR
(AP + BP) + CQ = (AR + CR) + BQ
AB + CQ = AC + BQ
But AB = AC
Therefore, CQ = BQ or BQ = CQ

